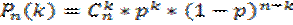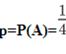Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения независимых событий ⇐ ПредыдущаяСтр 4 из 4
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий
Задача. На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме “Вписанная окружность”, равна 0,15. Вероятность того, что это вопрос по теме “Тригонометрия”, равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение. Вероятность того, что попадется вопрос по теме “Вписанная окружность” ИЛИ по теме “Тригонометрия”, равна СУММЕ этих вероятностей, то есть 0,15+0,3=0,45
Ответ: 0,45
Теорема сложения Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
Замечание: При использовании формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т.е., если условная вероятность события В равна его безусловной вероятности Заметим, что если при определении нового события,мы употребляем союз «ИЛИ», то имеет место сумма некоторых событий. Задача. На автогонках при заезде на первой автомашине вероятность победить
Решение. 2) Найдём вероятность того, что победит одна из двух автомашин:
Ответ: 0,96
Решение задач Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный? Решение. Общее число различных исходов есть n =1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле, получим
Задача 2. В корзине 9 красных шаров и 3 синих. Шары различаются только цветом. Наугад (не глядя) достаём один из них. Какова вероятность того, что выбранный таким образом шар окажется синего цвета? Решение. Теперь вычислим вероятность выбора синего шара.
Задача 3. Решение. Задача 4. Решение. Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: P(A×B) = 0,52 · 0,3 = 0,156. Задача 5. Решение. Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3 · 0,3 = 0,09. Формула Бернулли При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
*включение приборов (ламп, станков и т.п.) с заранее заданной одинаковой вероятностью выхода из строя каждого;
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А вединичном испытании буквой p, т.е. p=P(A), а вероятность противоположного события (событие А не наступило) - буквой q=P( Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли Распределение числа успехов (появлений события) носит название биномиального распределения.
Глава 6. Пример использования теории вероятностей в жизни Единый государственный экзамен и государственная итоговая аттестация Я сегодня обучаюсь в 10А классе, и на следующий год мне предстоит сдавать экзамены. Экзаменационные работы по различным предметам имеют свои особенности, но во всех из них, в том числе и по математике в 9 классе в части 1 даны задания с выбором ответа. Среди нерадивых учеников возник вопрос: «А нельзя ли выбрать наугад ответ и при этом получить положительную оценку за экзамен?» Я провела опрос среди обучающихся 10 классов: можно ли практически угадать задания, т.е. сдать ОГЭ по математике без подготовки. Результаты такие:53,2% респондентов считают, что смогут сдать экзамен указанным выше способом. Я решила проверить, правы ли они? Ответить на этот вопрос можно путем использования элементов теории вероятностей. Я хочу проверить это на примере предметов, обязательных для сдачи экзаменов: математика и русский язык и на примере наиболее предпочитаемых предметов в 11 классе. По данным 2012 года 51,4% выпускников ХМАО и 60,9% выпускников РФ выбрали обществознание.
Русский язык По данному предмету тест включает 39 заданий типа А,В и С, из которых 30 заданий типа А с выбором ответа из 4-х предложенных.Для того, чтобы пройти порок на экзамене в 2012 году достаточно было в 1 части правильно выполнить 14 заданий. Каждое задание имело 4 варианта ответов, один из которых правильный. Определить вероятность получения положительной оценки на экзамене можно по формуле Бернулли: Схема Бернулли описывает эксперименты со случайным исходом, заключающиеся в следующем.Проводятся n последовательных независимых одинаковых экспериментов, в каждом из которых выделяется одно и тоже событие А, которое может наступить или не наступить в ходе эксперимента. Так как испытания одинаковы, то в любом из них событие А наступает с одинаковой вероятностью. Обозначим ее р = Р(А). Вероятность дополнительного события обозначим q. Тогда q = P(Ā) = 1-p Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании первой части. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т.е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда Вероятность получения положительной оценки: 0,163% На примере демонстрационного варианта теста я предложила обучающимся 11А класса выбрать ответы путем угадывания.
Обществознание Первая часть демонстрационного варианта ЕГЭ по обществознанию содержит 20 заданий с выбором ответа, из которых только один верный. Определим вероятность получения положительной оценки. Установлен минимальный первичный балл по обществознанию – 15. Таким образом, вероятность благополучного исхода примерно равна 0,0003%! Я попросила обучающихся 11А класса угадать ответы по обществознанию. Ни один обучающийся не смог набрать нужное количество баллов по обществознанию. Математика В демонстрационный вариант КИМ ГИА (в новой форме) по МАТЕМАТИКЕ содержал 23 задания, из которых 9 заданий с выбором ответа и установления соответствия. Для успешной сдачи экзамена необходимо было решить не менее 8 заданий. Применим формулу Бернулли. Вывод: вероятность получения положительной оценки составляет 0,01%. Эксперимент, проведенный, среди учеников 11 классапоказал, что самое большое количество совпадений - 4. Экспериментальная часть Анкетирование Анкетирование проводилось среди обучающихся 10-х классов. Им было предложено ответить на следующие вопросы: 1.Можно ли сдать экзамены без подготовки, угадывая ответ в заданиях типа А? Результаты проведенного опроса отражены в диаграмме. Эксперимент 1.Среди обучающихся 11А класса на примере демонстрационного варианта контрольно-измерительных материалов провела эксперимент с угадыванием ответа по русскому языку и обществознанию. Результаты отражены в таблице.
В результате проведенного эксперимента применяя формулу Бернулли, я доказала, что сдать экзамены путем угадывания ответа невозможно. Только планомерная, вдумчивая и добросовестная учеба в школе позволит выпускнику хорошо подготовиться к участию в ЕГЭ и ГИА, и успешно решить судьбоносную проблему при переходе на более высокий уровень обучения в вуз. Заключение В результате проделанной мной работы, я добилась реализации поставленных перед собой задач: *во-первых, поняла, что теория вероятностей - это огромный раздел науки математики и изучить его в один заход невозможно; *во-вторых, перебрав множество фактов из жизни, и проведя эксперименты, я поняла, что действительно с помощью теории вероятностей можно предсказать события, происходящие в различных сферах жизнедеятельности; *в-третьих, исследовав вероятность успешной сдачи обучающимися 11 классов ЕГЭ и 9-ми классами ГИА по математике, я пришла к выводу, что только планомерная, вдумчивая и добросовестная учеба в школе позволит выпускнику хорошо подготовиться к участию в ЕГЭ. Таким образом, выдвинутая мной гипотеза подтвердилась, с помощью теории вероятностей я доказала, что к экзаменам надо готовиться, а не рассчитывать на авось.
Вывод 1. Я проанализировала учебный материал по математике и выделилатот материал, который раскрывает мою тему более подробно; 2. Рассмотрела задачи в учебной, научной литературе и сети интернет; 3. Выявила важность теории вероятностей в жизни человека
Библиографический список 1) Учебник по алгебре за 9 класс; авторы: Макарычев Ю.Н., Миндюк Н.Г.; 288 страниц 2) Учебник по алгебре за 9 класс; авторы: Дорофеев Г.В., Суворова С.Б.,; 336 страниц 3) https://bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/) 4) http://www.mathematics.ru/courses/algebra/content/chapter4/section3/paragraph1/theory.html 5) http://ru.wikipedia.org/wiki 6)https://ru.wikipedia.org/wiki 7) www.fipi.ru
|
||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.22.169 (0.023 с.) |
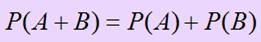

 , при заезде на второй автомашине
, при заезде на второй автомашине  . Найти:
. Найти: 

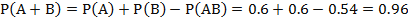
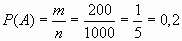
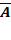 )=1−p.
)=1−p.