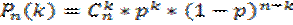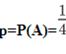Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. История возникновения теории вероятностейСодержание книги
Поиск на нашем сайте
Работу выполнила Чендей Елизавета, обучающаяся 10 класса
Руководитель Оганисян Ирина Михайловна, учитель математики средней школы № 12
ЯРОСЛАВЛЬ 2020 ГОД
Введение Актуальность темы: Теория вероятностей и математическая статистика – это наука, занимающаяся изучением закономерностей массовых случайных явлений, то есть статистических закономерностей. Такие же закономерности, только в более узкой предметной области социально-экономических явлений, изучает статистика. Между этими науками имеется общность методологии и высокая степень взаимосвязи. Практически любые выводы, сделанные статистикой, рассматриваются как вероятностные. С развитием рынка постепенно сращивается вероятность и статистика, особенно наглядно это проявляется в управлении рисками, товарными запасами, портфелем ценных бумаг и т.п. Характерным для современного этапа развития естественных и технических наук является весьма широкое применение статистических методов во всех областях знания. В настоящее время нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы. Целые разделы современной физики базируются на методах теории вероятностей. Все шире применяется вероятностные методы в современной электротехнике и радиотехнике, метеорологии и астрономии, теории автоматического регулирования и машиной математике. Обширное поле применения находит теория вероятностей в разнообразных областях военной технике: теория стрельбы бомбометании, теория прицелов и приборов управления огнем и множество других разделов военной науки широко используются методами теории вероятностей и ее математическим аппаратом. Таким образом, выбранная тема работы актуальна.
Гипотеза исследования:
С помощью теории вероятностей нельзя с большой степенью уверенности предсказать события, происходящие в нашей жизни.
Цель исследования:
Изучить материал по теме «Теории вероятностей», и выявить ее важности в жизни Задачи: 1. проанализировать учебный материала по математике и выделить тот материал, который раскрывает мою тему более подробно; 2. рассмотреть задачи в учебной, научной литературе и сети интернет; 3. определить важность теории вероятностей в жизни человека 4. провести эксперимент 5. сделать пособие по подготовке к ЕГЭ Объект исследования: Повседневная жизнь человека Предмет исследования: Теория вероятностей
Методы исследования: · теоретический · логический · экспериментальный · анализ · синтез Личный вклад: Я обобщила информацию о теории вероятностей и представила ее в реферате. Провела опрос и эксперимент среди обучающихся 9-х и 11-х классов. Я проанализировала результаты и сделала выводы, а так же представила информацию в виде диаграммы и таблицы.
Астрономия.
Именно для использования в астрономии был разработан знаменитый “метод наименьших квадратов” (Лежандр 1805, Гаусс 1815). Главной задачей, для решения которой он был первоначально использован, стал расчет орбит комет, который приходилось производить по малому числу наблюдений. Ясно, что надежное определение типа орбиты (эллипс или гипербола) и точный расчет ее параметров оказывается трудным, так как орбита наблюдается лишь на небольшом участке. Метод оказался эффективным, универсальным, и вызвал бурные споры о приоритете. Его стали использовать в геодезии и картографии. Сейчас, когда искусство ручных расчетов утрачено, трудно представить, что при составлении карт мирового океана в 1880-х годах в Англии методом наименьших квадратов была численно решена система, состоящая из примерно 6000 уравнений с несколькими сотнями неизвестных.
Физика. Во второй половине 19 века была в работах Максвелла, Больцмана и Гиббса была развита статистическая механика, которая описывала состояние разряженных систем, содержащих огромное число частиц (порядка числа Авогадро). Если раньше понятие распределения случайной величины было преимущественно связано с распределением ошибок измерения, то теперь распределенными оказались самые разные величины – скорости, энергии, длины свободного пробега.
Биометрия. В 1870-1900 годах бельгиец Кетле и англичане Френсис Гальтон и Карл Пирсон основали новое научное направление – биометрию, в которой впервые стала систематически и количественно изучаться неопределенная изменчивость живых организмов и наследование количественных признаков. В научный оборот были введены новые понятия – регрессии и корреляции. Итак, вплоть до начала 20 века основные приложения теории вероятности были связаны с научными исследованиями. Внедрение в практику – сельское хозяйство, промышленность, медицину произошло в 20 веке.
Сельское хозяйство. В начале 20 века в Англии была поставлена задача количественного сравнения эффективности различных методов ведения сельского хозяйства. Для решения этой задачи была развита теория планирования экспериментов, дисперсионный анализ. Основная заслуга в развитии этого уже чисто практического использования статистики принадлежит сэру Рональду Фишеру, астроному по образованию, а в дальнейшем фермеру, статистику, генетику, президенту английского Королевского общества. Современная математическая статистика, пригодная для широкого применения в практике, была развита в Англии (Карл Пирсон, Стьюдент, Фишер). Стьюдент впервые решил задачу оценки неизвестного параметра распределения без использования байесовского подхода. Промышленность. Введение методов статистического контроля на производстве (контрольные карты Шухарта). Сокращение необходимого количества испытаний качества продукции. Математические методы оказываются уже настолько важными, что их стали засекречивать. Так книга с описанием новой методики, позволявшей сократить количество испытаний (“Последовательный анализ” Вальда), была издана только после окончания второй мировой войны в 1947 году.
Медицина. Широкое применение статистических методов в медицине началось сравнительно недавно (вторая половина 20 века). Развитие эффективных методов лечения (антибиотики, инсулин, эффективная анестезия, искусственное кровообращение) потребовало достоверных методов оценки их эффективности. Возникло новое понятие “Доказательная медицина”. Начал развиваться более формальный, количественный подход к терапии многих заболевании – введение протоколов.
С середины 1980-х годов возник новый и важнейший фактор, революционизировавший все приложения теории вероятностей – возможность широкого использования быстрых и доступных компьютеров. Почувствовать всю громадность произошедшего переворота можно, если учесть, что один современный персональный компьютер превосходит по быстродействию и памяти все компьютеры СССР и США, имевшиеся к 1968 году, времени, когда уже были осуществлены проекты, связанные со строительством атомных электростанций, полетами на Луну, созданием термоядерной бомбы. Свойства
Игры в кости Инструментом для игры являются кубики (кости) в количестве от одного до пяти в зависимости от вида игры. Суть игры состоит в выбрасывании кубиков и дальнейшем подсчёте очков, количество которых и определяет победителя. Основной принцип игры в кости — каждый игрок по очереди бросает некоторое количество игральных костей (от одной до пяти), после чего результат броска (сумма выпавших очков; в некоторых вариантах используются очки каждой кости по отдельности) используется для определения победителя или проигравшего. Лотерея Лотерея - организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота). Карточные игры Карточная игра — игра с применением игральных карт, характеризуется случайным начальным состоянием, для определения которого используется набор (колода). Важным принципом практически всех карточных игр является случайность порядка карт в колоде. Игровые автоматы Известно, что в игровых автоматах скорость вращения барабанов зависит от работы микропроцессора, повлиять на который нельзя. Но можно вычислить вероятность выигрыша на игровом автомате, в зависимости от количества символов на нем, числа барабанов и других условий. Однако выиграть это знание вряд ли поможет. В наше время наука о случайном очень важна. Она применяется в селекции при разведении ценных сортов растений, при приемке промышленной продукции, при расчете графика разгрузки вагонов и т.д. Теорема умножения Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
Заметим, что если при определении нового события, употребляем союз «И», то имеет место произведение некоторых событий. Задача. В читальном зале имеется 6 учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете. Решение. Рассмотрим следующие события: А1- первый взятый учебник в переплете; A2- второй взятый учебник в переплете. Событие, состоящее в том, что оба взятых учебника в переплете
Вероятность наступления события А1 p(A1) в соответствии с классическим определением вероятности:
Вероятность наступления события А2 определяется условной вероятностью наступления события А2 при условии наступления события А1, т.е. Тогда искомая вероятность наступления события: P(A)=0,5*0,4=0,2. Ответ: 0,2 Решение задач Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный? Решение. Общее число различных исходов есть n =1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле, получим
Задача 2. В корзине 9 красных шаров и 3 синих. Шары различаются только цветом. Наугад (не глядя) достаём один из них. Какова вероятность того, что выбранный таким образом шар окажется синего цвета? Решение. Теперь вычислим вероятность выбора синего шара. Задача 3. Решение. Задача 4. Решение. Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: P(A×B) = 0,52 · 0,3 = 0,156. Задача 5.
Решение. Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3 · 0,3 = 0,09. Формула Бернулли При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
*включение приборов (ламп, станков и т.п.) с заранее заданной одинаковой вероятностью выхода из строя каждого;
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А вединичном испытании буквой p, т.е. p=P(A), а вероятность противоположного события (событие А не наступило) - буквой q=P( Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли Распределение числа успехов (появлений события) носит название биномиального распределения.
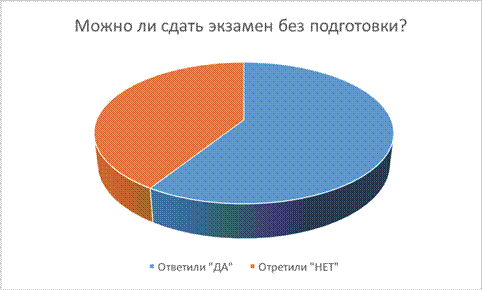
Глава 6. Пример использования теории вероятностей в жизни Единый государственный экзамен и государственная итоговая аттестация Я сегодня обучаюсь в 10А классе, и на следующий год мне предстоит сдавать экзамены. Экзаменационные работы по различным предметам имеют свои особенности, но во всех из них, в том числе и по математике в 9 классе в части 1 даны задания с выбором ответа. Среди нерадивых учеников возник вопрос: «А нельзя ли выбрать наугад ответ и при этом получить положительную оценку за экзамен?» Я провела опрос среди обучающихся 10 классов: можно ли практически угадать задания, т.е. сдать ОГЭ по математике без подготовки. Результаты такие:53,2% респондентов считают, что смогут сдать экзамен указанным выше способом. Я решила проверить, правы ли они? Ответить на этот вопрос можно путем использования элементов теории вероятностей. Я хочу проверить это на примере предметов, обязательных для сдачи экзаменов: математика и русский язык и на примере наиболее предпочитаемых предметов в 11 классе. По данным 2012 года 51,4% выпускников ХМАО и 60,9% выпускников РФ выбрали обществознание.
Русский язык По данному предмету тест включает 39 заданий типа А,В и С, из которых 30 заданий типа А с выбором ответа из 4-х предложенных.Для того, чтобы пройти порок на экзамене в 2012 году достаточно было в 1 части правильно выполнить 14 заданий. Каждое задание имело 4 варианта ответов, один из которых правильный. Определить вероятность получения положительной оценки на экзамене можно по формуле Бернулли: Схема Бернулли описывает эксперименты со случайным исходом, заключающиеся в следующем.Проводятся n последовательных независимых одинаковых экспериментов, в каждом из которых выделяется одно и тоже событие А, которое может наступить или не наступить в ходе эксперимента. Так как испытания одинаковы, то в любом из них событие А наступает с одинаковой вероятностью. Обозначим ее р = Р(А). Вероятность дополнительного события обозначим q. Тогда q = P(Ā) = 1-p Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании первой части. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т.е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда Вероятность получения положительной оценки: 0,163% На примере демонстрационного варианта теста я предложила обучающимся 11А класса выбрать ответы путем угадывания. Обществознание Первая часть демонстрационного варианта ЕГЭ по обществознанию содержит 20 заданий с выбором ответа, из которых только один верный. Определим вероятность получения положительной оценки. Установлен минимальный первичный балл по обществознанию – 15. Таким образом, вероятность благополучного исхода примерно равна 0,0003%! Я попросила обучающихся 11А класса угадать ответы по обществознанию. Ни один обучающийся не смог набрать нужное количество баллов по обществознанию. Математика В демонстрационный вариант КИМ ГИА (в новой форме) по МАТЕМАТИКЕ содержал 23 задания, из которых 9 заданий с выбором ответа и установления соответствия. Для успешной сдачи экзамена необходимо было решить не менее 8 заданий. Применим формулу Бернулли. Вывод: вероятность получения положительной оценки составляет 0,01%. Эксперимент, проведенный, среди учеников 11 классапоказал, что самое большое количество совпадений - 4. Экспериментальная часть Анкетирование Анкетирование проводилось среди обучающихся 10-х классов. Им было предложено ответить на следующие вопросы: 1.Можно ли сдать экзамены без подготовки, угадывая ответ в заданиях типа А? Результаты проведенного опроса отражены в диаграмме. Эксперимент 1.Среди обучающихся 11А класса на примере демонстрационного варианта контрольно-измерительных материалов провела эксперимент с угадыванием ответа по русскому языку и обществознанию. Результаты отражены в таблице.
В результате проведенного эксперимента применяя формулу Бернулли, я доказала, что сдать экзамены путем угадывания ответа невозможно. Только планомерная, вдумчивая и добросовестная учеба в школе позволит выпускнику хорошо подготовиться к участию в ЕГЭ и ГИА, и успешно решить судьбоносную проблему при переходе на более высокий уровень обучения в вуз. Заключение В результате проделанной мной работы, я добилась реализации поставленных перед собой задач: *во-первых, поняла, что теория вероятностей - это огромный раздел науки математики и изучить его в один заход невозможно; *во-вторых, перебрав множество фактов из жизни, и проведя эксперименты, я поняла, что действительно с помощью теории вероятностей можно предсказать события, происходящие в различных сферах жизнедеятельности; *в-третьих, исследовав вероятность успешной сдачи обучающимися 11 классов ЕГЭ и 9-ми классами ГИА по математике, я пришла к выводу, что только планомерная, вдумчивая и добросовестная учеба в школе позволит выпускнику хорошо подготовиться к участию в ЕГЭ. Таким образом, выдвинутая мной гипотеза подтвердилась, с помощью теории вероятностей я доказала, что к экзаменам надо готовиться, а не рассчитывать на авось. Вывод 1. Я проанализировала учебный материал по математике и выделилатот материал, который раскрывает мою тему более подробно; 2. Рассмотрела задачи в учебной, научной литературе и сети интернет; 3. Выявила важность теории вероятностей в жизни человека
Библиографический список 1) Учебник по алгебре за 9 класс; авторы: Макарычев Ю.Н., Миндюк Н.Г.; 288 страниц 2) Учебник по алгебре за 9 класс; авторы: Дорофеев Г.В., Суворова С.Б.,; 336 страниц 3) https://bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/) 4) http://www.mathematics.ru/courses/algebra/content/chapter4/section3/paragraph1/theory.html 5) http://ru.wikipedia.org/wiki 6)https://ru.wikipedia.org/wiki 7) www.fipi.ru
Приложения Диаграмма
Таблица Всего в опросе участвовали 29 человек
Работу выполнила Чендей Елизавета, обучающаяся 10 класса
Руководитель Оганисян Ирина Михайловна, учитель математики средней школы № 12
ЯРОСЛАВЛЬ 2020 ГОД
Введение Актуальность темы: Теория вероятностей и математическая статистика – это наука, занимающаяся изучением закономерностей массовых случайных явлений, то есть статистических закономерностей. Такие же закономерности, только в более узкой предметной области социально-экономических явлений, изучает статистика. Между этими науками имеется общность методологии и высокая степень взаимосвязи. Практически любые выводы, сделанные статистикой, рассматриваются как вероятностные. С развитием рынка постепенно сращивается вероятность и статистика, особенно наглядно это проявляется в управлении рисками, товарными запасами, портфелем ценных бумаг и т.п. Характерным для современного этапа развития естественных и технических наук является весьма широкое применение статистических методов во всех областях знания. В настоящее время нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы. Целые разделы современной физики базируются на методах теории вероятностей. Все шире применяется вероятностные методы в современной электротехнике и радиотехнике, метеорологии и астрономии, теории автоматического регулирования и машиной математике. Обширное поле применения находит теория вероятностей в разнообразных областях военной технике: теория стрельбы бомбометании, теория прицелов и приборов управления огнем и множество других разделов военной науки широко используются методами теории вероятностей и ее математическим аппаратом. Таким образом, выбранная тема работы актуальна.
Гипотеза исследования:
С помощью теории вероятностей нельзя с большой степенью уверенности предсказать события, происходящие в нашей жизни.
Цель исследования:
Изучить материал по теме «Теории вероятностей», и выявить ее важности в жизни Задачи: 1. проанализировать учебный материала по математике и выделить тот материал, который раскрывает мою тему более подробно; 2. рассмотреть задачи в учебной, научной литературе и сети интернет; 3. определить важность теории вероятностей в жизни человека 4. провести эксперимент 5. сделать пособие по подготовке к ЕГЭ Объект исследования: Повседневная жизнь человека Предмет исследования: Теория вероятностей
Методы исследования: · теоретический · логический · экспериментальный · анализ · синтез Личный вклад: Я обобщила информацию о теории вероятностей и представила ее в реферате. Провела опрос и эксперимент среди обучающихся 9-х и 11-х классов. Я проанализировала результаты и сделала выводы, а так же представила информацию в виде диаграммы и таблицы.
Глава 1. История возникновения теории вероятностей Французский дворянин, некий господин де Мере, был азартным игроком в кости и страстно хотел разбогатеть. Он затратил много времени, чтобы открыть тайну игры в кости. Он выдумывал различные варианты игры, предполагая, что таким образом приобретет крупное состояние. Так, например, он предлагал бросать одну кость по очереди 4 раза и убеждал партнера, что по крайней мере один раз выпадет при этом шестерка. Если за 4 броска шестерка не выходила, то выигрывал противник. В те времена еще не существовала отрасль математики, которую сегодня мы называем теорией вероятностей, а поэтому, чтобы убедиться, верны ли его предположения, господин Мере обратился к своему знакомому, известному математику и философу Б. Паскалю с просьбой, чтобы он изучил два знаменитых вопроса, первый из которых он попытался решить сам. Вопросы были такие: Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний? Как справедливо разделить поставленные на кон двумя игроками деньги, если они по каким-то причинам прекратили игру преждевременно? Паскаль не только сам заинтересовался этим, но и написал письмо известному математику П. Ферма, чем спровоцировал его заняться общими законами игры в кости и вероятностью выигрыша. Таким образом, азарт и жажда разбогатеть дали толчок возникновению новой чрезвычайно существенной математической дисциплины: теории вероятностей. В разработке ее основ принимали участие математики такого масштаба, как Паскаль и Ферма, Гюйгенс (1629—1695), который написал тракта «О расчетах при азартных играх», Яков Бернулли (1654—1705), Муавр (1667—1754), Лаплас (1749— 1827), Гаусс (1777—1855) и Пуассон (1781—1840). В наше время теория вероятности используется почти во всех отраслях знаний: в статистике, синоптике (прогноз погоды), биологии, экономике, технологии, строительстве и т. д.
Глава 2. Применение теории вероятностей в XIX-XX веках В 19 и 20 столетиях теория вероятностей проникает сначала в науку (астрономию, физику, биологию), потом в практику (сельское хозяйство, промышленность, медицину), и наконец, после изобретения компьютеров, в повседневную жизнь любого человека, пользующегося современными средствами получения и передачи информации. Проследим применение в различных областях.
Астрономия. Именно для использования в астрономии был разработан знаменитый “метод наименьших квадратов” (Лежандр 1805, Гаусс 1815). Главной задачей, для решения которой он был первоначально использован, стал расчет орбит комет, который приходилось производить по малому числу наблюдений. Ясно, что надежное определение типа орбиты (эллипс или гипербола) и точный расчет ее параметров оказывается трудным, так как орбита наблюдается лишь на небольшом участке. Метод оказался эффективным, универсальным, и вызвал бурные споры о приоритете. Его стали использовать в геодезии и картографии. Сейчас, когда искусство ручных расчетов утрачено, трудно представить, что при составлении карт мирового океана в 1880-х годах в Англии методом наименьших квадратов была численно решена система, состоящая из примерно 6000 уравнений с несколькими сотнями неизвестных.
Физика. Во второй половине 19 века была в работах Максвелла, Больцмана и Гиббса была развита статистическая механика, которая описывала состояние разряженных систем, содержащих огромное число частиц (порядка числа Авогадро). Если раньше понятие распределения случайной величины было преимущественно связано с распределением ошибок измерения, то теперь распределенными оказались самые разные величины – скорости, энергии, длины свободного пробега.
Биометрия. В 1870-1900 годах бельгиец Кетле и англичане Френсис Гальтон и Карл Пирсон основали новое научное направление – биометрию, в которой впервые стала систематически и количественно изучаться неопределенная изменчивость живых организмов и наследование количественных признаков. В научный оборот были введены новые понятия – регрессии и корреляции. Итак, вплоть до начала 20 века основные приложения теории вероятности были связаны с научными исследованиями. Внедрение в практику – сельское хозяйство, промышленность, медицину произошло в 20 веке.
Сельское хозяйство. В начале 20 века в Англии была поставлена задача количественного сравнения эффективности различных методов ведения сельского хозяйства. Для решения этой задачи была развита теория планирования экспериментов, дисперсионный анализ. Основная заслуга в развитии этого уже чисто практического использования статистики принадлежит сэру Рональду Фишеру, астроному по образованию, а в дальнейшем фермеру, статистику, генетику, президенту английского Королевского общества. Современная математическая статистика, пригодная для широкого применения в практике, была развита в Англии (Карл Пирсон, Стьюдент, Фишер). Стьюдент впервые решил задачу оценки неизвестного параметра распределения без использования байесовского подхода. Промышленность. Введение методов статистического контроля на производстве (контрольные карты Шухарта). Сокращение необходимого количества испытаний качества продукции. Математические методы оказываются уже настолько важными, что их стали засекречивать. Так книга с описанием новой методики, позволявшей сократить количество испытаний (“Последовательный анализ” Вальда), была издана только после окончания второй мировой войны в 1947 году.
Медицина. Широкое применение статистических методов в медицине началось сравнительно недавно (вторая половина 20 века). Развитие эффективных методов лечения (антибиотики, инсулин, эффективная анестезия, искусственное кровообращение) потребовало достоверных методов оценки их эффективности. Возникло новое понятие “Доказательная медицина”. Начал развиваться более формальный, количественный подход к терапии многих заболевании – введение протоколов. С середины 1980-х годов возник новый и важнейший фактор, революционизировавший все приложения теории вероятнос
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.95.129 (0.016 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


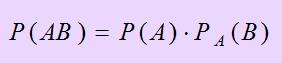
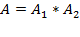 . События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий:
. События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий: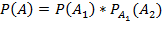 .
.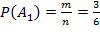 =0.5
=0.5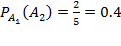
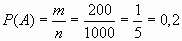
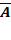 )=1−p.
)=1−p.