Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Теория вероятностей в азартных играхСодержание книги
Поиск на нашем сайте
Игры в кости Инструментом для игры являются кубики (кости) в количестве от одного до пяти в зависимости от вида игры. Суть игры состоит в выбрасывании кубиков и дальнейшем подсчёте очков, количество которых и определяет победителя. Основной принцип игры в кости — каждый игрок по очереди бросает некоторое количество игральных костей (от одной до пяти), после чего результат броска (сумма выпавших очков; в некоторых вариантах используются очки каждой кости по отдельности) используется для определения победителя или проигравшего. Лотерея Лотерея - организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота). Карточные игры Карточная игра — игра с применением игральных карт, характеризуется случайным начальным состоянием, для определения которого используется набор (колода). Важным принципом практически всех карточных игр является случайность порядка карт в колоде. Игровые автоматы Известно, что в игровых автоматах скорость вращения барабанов зависит от работы микропроцессора, повлиять на который нельзя. Но можно вычислить вероятность выигрыша на игровом автомате, в зависимости от количества символов на нем, числа барабанов и других условий. Однако выиграть это знание вряд ли поможет. В наше время наука о случайном очень важна. Она применяется в селекции при разведении ценных сортов растений, при приемке промышленной продукции, при расчете графика разгрузки вагонов и т.д. Глава 5. Формулы теории вероятностей Теорема умножения Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
Заметим, что если при определении нового события, употребляем союз «И», то имеет место произведение некоторых событий. Задача. В читальном зале имеется 6 учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете. Решение. Рассмотрим следующие события: А1- первый взятый учебник в переплете; A2- второй взятый учебник в переплете. Событие, состоящее в том, что оба взятых учебника в переплете
Вероятность наступления события А1 p(A1) в соответствии с классическим определением вероятности:
Вероятность наступления события А2 определяется условной вероятностью наступления события А2 при условии наступления события А1, т.е. Тогда искомая вероятность наступления события: P(A)=0,5*0,4=0,2. Ответ: 0,2
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.206 (0.006 с.) |

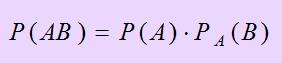
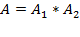 . События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий:
. События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий: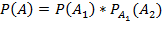 .
.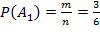 =0.5
=0.5