Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распознаватель на основе алгоритма «сдвиг-свёртка»
Этот распознаватель строится на основе расширенного МПА с одним состоянием q: R({q},V,Z,d,q, e,{q}). Автомат распознаёт цепочки КС-языка, задаваемого грамматикой G(VT,VN,P,S). Входной алфавит автомата содержит терминальные символы грамматики V=VT, а алфавит магазинных символов Z=VTÈVN. Начальная конфигурация автомата (q,a, e), т.е. считывающая головка находится в начале входной цепочки aÎVT*, а стек пуст. Конечная конфигурация автомата (q, e,S), т.е. в стеке находится целевой символ. Функция перехода строится на основе правил P грамматики G: 1. Если правило (A ® m)ÎP, то (q,A)Îd(q, e,m), AÎVN, mÎ(VTÈVN)*. 2. "aÎVT (q,a)Îd(q,a, e). Работу автомата можно описать следующим образом. Если на верхушке стека находится цепочка символов m, то ее можно заменить на нетерминальный символ A, если (A ® m)ÎP, не сдвигая считывающую головку автомата. Этот шаг работы алгоритма называется «свёртка». С другой стороны, если считывающая головка обозревает символ входной цепочки a, то его можно поместить в стек, а считывающую головку передвинуть на один символ вправо. Данный шаг называется «сдвиг» или «перенос». Алгоритм называется «сдвиг-свёртка» или «перенос-свёртка». Данный расширенный автомат строит правосторонние выводы для грамматики G, читает цепочку входных символов слева направо, поэтому строит дерево снизу вверх. Такой распознаватель является восходящим. Для моделирования такого автомата необходимо, чтобы грамматика не содержала цепных правил и e-правил. Как было рассмотрено ранее, к такому виду может быть приведена любая КС-грамматика, поэтому алгоритм является универсальным. Рассмотренный автомат имеет больше неоднозначностей, чем распознаватель, основанный на выборе альтернатив. На каждом шаге работы автомата должны быть решены следующие вопросы: § что необходимо выполнить – сдвиг или свёртку; § если выполнять свёртку, то какую цепочку m выбрать для поиска правил (эта цепочка должна находиться в правой части правил); § какое из правил выбрать для свёртки, если в грамматике окажется более одного правила вида (A ® m)ÎP с одинаковой правой частью и различными левыми частями A. Чтобы промоделировать работу этого расширенного МПА, надо на каждом шаге запоминать все предпринятые действия, чтобы иметь возможность при необходимости вернуться к уже сделанному шагу и проделать все действия иначе. Таким образом должны быть перебраны все возможные варианты.
Рассмотрим один из возможных вариантов реализации алгоритма. Распознаватель с возвратами на основе алгоритма «сдвиг-свёртка» Для работы алгоритма используется расширенный МПА, построенный на основе исходной КС-грамматики G(VT,VN,P,S). Все правила из множества P перенумеруем слева направо и сверху вниз в порядке их записи в форме Бэкуса-Наура. Входная цепочка имеет вид a=a1a2…an, ½a½= n, aiÎVT "i. Аналогично алгоритму нисходящего распознавателя, в рассматриваемом алгоритме используется дополнительное состояние b и стек возвратов L2. Этот стек может содержать номера правил грамматики, использованных для свёртки, если на очередном шаге алгоритма выполнялась свёртка, или 0, если на очередном шаге выполнялся сдвиг.
Состояние алгоритма на каждом шаге определяется четырьмя параметрами: (Q,i,L1,L2), где Q – текущее состояние автомата (q или b), i – положение считывающей головки во входной цепочке a (1 < i £ n+1), L1 и L2 – содержимое стеков. Начальным состоянием алгоритма является (q,1,e,e). Алгоритм начинает работу с начального состояния и циклически выполняет 5 шагов до тех пор, пока не перейдёт в конечное состояние или не обнаружит ошибку. Конечное состояние алгоритма (q,n+1,S,g). Алгоритм выполняет циклически следующие шаги: Шаг 1 («Попытка свертки»): (q, i, mb, g) ® (q, i, mA, jg), где bÎ(VNÈVT)*, g – содержимое стека возвратов L2, если (A ® b)ÎP – первое из всех возможных правил из множества P с номером j для подцепочки b, причём оно является первым подходящим правилом для цепочки mb, для которой правило вида A ® b существует (заменяем цепочку в стеке МПА на нетерминал – «сворачиваем» её, а в стек возврата записываем номер использованного правила). Если удалось выполнить свёртку, то возвращаемся к шагу 1, иначе переходим к шагу 2.
Шаг 2 («Перенос-сдвиг»): Если i < n+1, то (q, i, m, g) ® (q, i+1, mai, 0g), где aiÎVT. Если i = n+1, то идти дальше, иначе перейти к шагу 1. Шаг 3 («Завершение»): Если состояние алгоритма (q, n+1, S, g), то разбор завершён и алгоритм заканчивает работу, иначе перейти к шагу 4. Шаг 4 («Переход к возврату»): (q, n+1, m, g) ® (b, n+1, m, g). Шаг 5 («Возврат»): При возврате возможны следующие варианты: 1) Если исходное состояние алгоритма (b, i, mA, jg) (j>0): § Перейти (b, i, mA, jg) ® (q, i, m¢B, kg), если (A ® b)ÎP – это правило с номером j и существует правило (B ® b¢)ÎP с номером k, k>j, такое, что mb=m¢b¢, после чего вернуться к шагу 1. § Перейти (b, i, mA, jg) ® (b, n+1, mb, g), если i=n+1, (A ® b)ÎP – это правило с номером j и не существует других правил из множества P с номером k, k>j, таких, что их правая часть является суффиксом цепочки mb, после этого вернуться к шагу 5. § Перейти (b, i, mA, jg) ® (q, i+1, mbai, 0g), где aiÎVT, если i¹n+1, (A ® b)ÎP – это правило с номером j и не существует других правил из множества P с номером k>j, таких, что их правая часть является правой подцепочкой из цепочки mb, после этого перейти к шагу 1. § Иначе сигнализировать об ошибке и прекратить выполнение. 2) Если исходное состояние алгоритма (b, i, ma, 0g), aÎVT, то если i>1, тогда перейти в следующее состояние (b, i–1, m, g) и вернуться к шагу 5, иначе сигнализировать об ошибке и прекратить выполнение алгоритма. При успешном завершении алгоритма на основе содержимого стека возврата можно построить цепочку вывода. Для этого достаточно удалить из стека все 0 и будет получена последовательность номеров правил, используемых при выводе цепочки. Пример: Пусть дана грамматика для арифметических выражений: G ({+,–,/,*,a,b,(,)}, {S,T,E}, P, S), где правила P имеют вид: S ® S+T [1] ½S–T [2] ½T*E [3] ½T/E [4] ½(S) [5] ½a [6] ½b [7] T ® T*E [8] ½T/E [9] ½(S) [10] ½a [11] ½b [12] E ® (S) [13] ½a [14] ½b [15].
1) (q,1,e,e) |¾(2) (q,2, a,[0, e]) |¾(1) (q,2,S,[6,0]) |¾(2) (q,3,S+,[0,6,0]) |¾(2) (q,4,S+ b,[0,0,6,0]) |¾(1) (q,4,S+S,[7,0,0,6,0]) |¾(4) (b,4,S+ S,[ 7,0,0,6,0]) |¾(5) (q,4, S+T,[12,0,0,6,0]) |¾(1) (q,4,S,[1,12,0,0,6,0]) |¾(3) stop Алгоритм успешно завершён, в стеке возврата содержатся номера правил, которые участвовали в выводе цепочки: L2 = [1,12,0,0,6,0] = [1,12,6]. Þ цепочка вывода имеет вид S Þ S+T Þ S+b Þ a+b. Построим дерево вывода. 2) ‘a/(a–b)’:
Алгоритм успешно завершён, в стеке возврата содержатся номера правил: L2=[4,13,0,2,12,0,0,6,0,0,0,11,0]=[4,13,2,12,6,11]. Тогда цепочка вывода имеет вид: SÞT/EÞT/(S)ÞT/(S–T)ÞT/(S–b)ÞT/(a–b)Þa/(a–b). Дерево вывода строится аналогично построенному ранее.
Преимущества и недостатки рассмотренного алгоритма аналогичны тем, которые мы видели в методе нисходящего разбора с возвратами: это также просто реализуемый универсальный алгоритм, время работы которого экспоненциально зависит от длины входной цепочки. Как и алгоритм нисходящего распознавателя с возвратами, сам по себе алгоритм «сдвиг-свёртка» не используется в компиляторах, но его основные принципы лежат в основе многих восходящих распознавателей, строящих правосторонние выводы и работающих без возвратов. Оба рассмотренных распознавателя имеют приблизительно одинаковые показатели. Выбор того или иного алгоритма для реализации простейшего распознавателя зависит от грамматики языка.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.29.224 (0.016 с.) |
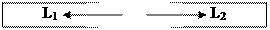В итоге алгоритм работает с двумя стеками, L1 – стек МПА и L2 – стек возвратов, причём первый содержит цепочку символов, а второй – целые числа от 0 до m, где m – количество правил грамматики. В цепочку стека L1 символы помещаются справа, а числа в стек L2 – слева.
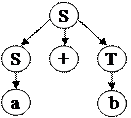Рассмотрим разбор двух цепочек: ‘a+b’ и ‘a/(a–b)’.
