
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распознаватели КС-языков с возвратомСодержание книги
Поиск на нашем сайте
Распознаватели КС-языков с возвратом представляют собой самый простой тип распознавателей, основанный на модели недетерминированного МП-автомата. Как известно, при работе такого автомата возможны альтернативные варианты его поведения. Существуют два варианта реализации алгоритма работы недетерминированного МПА. Первый вариант предполагает запоминание на каждом шаге работы всех возможных следующих состояний. Алгоритм моделирует работу автомата по одному из возможных переходов до тех пор, пока либо не будет достигнута конечная конфигурация автомата, либо возникнет ситуация, когда следующая конфигурация не определена. В последнем случае происходит возврат на несколько шагов назад в ту конфигурацию, из которой был возможен альтернативный вариант, и моделирование продолжается. Если какая-то из последовательностей шагов приводит к заключительной конфигурации, то цепочка считается принятой, а автомат заканчивает работу. Если все варианты работы перебраны, а конечная конфигурация не достигнута, то алгоритм завершается с ошибкой. Во втором варианте алгоритм моделирования МПА на каждом шаге работы при возникновении неоднозначности с несколькими возможными следующими состояниями должен запускать свою новую копию для обработки каждого из этих состояний. Если хотя бы одна из копий приводит в заключительную конфигурацию, то цепочка распознана и работа всех остальных копий также завершается. Если ни одна из копий не достигнет конечной конфигурации, алгоритм завершается с ошибкой и цепочка не принимается. Во втором варианте различные копии алгоритма должны выполняться параллельно, следовательно, необходимо наличие механизма управления параллельными процессами. Кроме того, количество копий алгоритма заранее неизвестно, их может быть много, в то время как количество одновременно выполняющихся процессов ограничено. Этим объясняется то, что большее распространение получил первый вариант алгоритма, который называется «разбором с возвратами». Хотя МПА представляет собой односторонний распознаватель, алгоритм моделирования его работы предусматривает возврат к уже прочитанной цепочке символов. Кроме того, любой практический алгоритм должен завершаться за конечное время. Алгоритм моделирования работы произвольного МПА в общем случае не удовлетворяет такому условию. Например, после считывания всей входной цепочки МПА может совершить произвольное число (может быть, и бесконечное) e-переходов. В таком случае, если входная цепочка не принята, алгоритм может никогда не завершиться. Для того чтобы избежать таких ситуаций, алгоритм работы МПА с возвратами строят не для произвольных автоматов, а для автоматов, удовлетворяющих некоторым заданным условиям. Обычно грамматику исходного языка подвергают сначала некоторым эквивалентным преобразованиям, приводя её к заранее заданному виду. Вычислительная сложность алгоритмов: Алгоритмы разбора с возвратами имеют экспоненциальную сложность, т.е. их вычислительные затраты экспоненциально зависят от длины входной цепочки символов. Обозначим эту цепочку a½aÎVT*, её длина ½a½= n. Конкретный характер зависимости определяется вариантом реализации алгоритма. В общем случае при первом варианте реализации время выполнения алгоритма для произвольной КС-грамматики имеет экспоненциальную, а необходимый объём памяти – линейную зависимость от длины входной цепочки: T=O(en), M=O(n). При втором варианте ситуация обратная – время имеет линейную зависимость, а требуемый объём памяти – экспоненциальную: T=O(n), M=O(en). В любом случае, непомерно большие вычислительные затраты на реализацию алгоритма существенно ограничивают возможности его применения. Для конкретных классов КС-языков существуют более эффективные алгоритмы распознавания. Основные варианты разбора с возвратом – это нисходящий распознаватель и распознаватель на основе алгоритма «сдвиг-свёртка». 4.3.1.1. Нисходящий распознаватель с возвратом (с подбором альтернатив) Этот распознаватель моделирует работу МПА с одним состоянием q: R({q}, V, Z, d, q, S, {q}). Автомат распознаёт цепочки КС-языка, задаваемого грамматикой G(VT,VN,P,S). Входной алфавит автомата содержит терминальные символы грамматики V=VT, а алфавит магазинных символов Z=VTÈVN. Начальная конфигурация автомата (q,a,S), где входная цепочка aÎVT*, а в стеке находится целевой символ грамматики. Конечная (заключительная) конфигурация автомата (q, e,e). Функция перехода строится на основе правил грамматики следующим образом: 1. Если правило (A ® m)ÎP, то (q,m)Îd(q, e,A), AÎVN, mÎ(VTÈVN)*. 2. "aÎVT (q, e)Îd(q,a,a). Работу автомата можно описать следующим образом. Если на верхушке стека находится нетерминальный символ A, то его можно заменить на цепочку символов m, если (A ® m)ÎP, не сдвигая при этом считывающую головку автомата. Этот шаг работы алгоритма называется «подбор альтернативы». Если на верхушке стека находится терминальный символ, совпадающий с текущим входным символом, то его можно выбросить из стека, а считывающую головку передвинуть на один символ вправо. Данный шаг называется «выброс». Если в грамматике окажется более одного правила вида (A ® m)ÎP с различными m, то функция будет содержать более одного следующего состояния, следовательно, у автомата будет несколько альтернатив. Рассмотренный автомат строит левосторонние выводы для грамматики G, следовательно, эта грамматика не должна быть леворекурсивной. Ранее было показано, что к нелеворекурсивному виду может быть приведена произвольная грамматика, следовательно, алгоритм является универсальным. Поскольку цепочка входных символов считывается слева направо, а вывод является левосторонним, дерево строится сверху вниз. Такой распознаватель называется нисходящим. На каждом шаге работы МП-автомата необходимо принимать решение о том, выполнять выброс или подбор альтернативы. Алгоритм должен иметь возможность выбирать поочерёдно все альтернативы, следовательно, необходимо хранить информацию о том, какие варианты уже использованы, чтобы вернуться к этому шагу и подобрать другие альтернативы. Такой алгоритм разбора называется алгоритмом с подбором альтернатив. Существует множество способов моделирования работы данного МП-автомата. Рассмотрим один из примеров его реализации. Алгоритм распознавателя с подбором альтернатив. Для работы алгоритма используется МПА, построенный на основе исходной КС-грамматики G(VT,VN,P,S). Все правила из множества P представим в виде A ® a1½a2½…½ak, т.е. для каждого нетерминального символа AÎVN перенумеруем все возможные альтернативы. Входная цепочка имеет вид a=a1a2…an, ½a½= n, aiÎVT "i. В алгоритме используется ещё одно дополнительное состояние b для обратного хода (back – возврат). Для хранения уже выбранных альтернатив используется дополнительный стек L2, который может содержать символы входного языка автомата aÎVT и символы вида Aj, где AÎVN – это будет означать, что среди всех возможных правил для символа A была выбрана альтернатива с номером j.
Состояние алгоритма на каждом шаге определяется четырьмя параметрами: (Q,i,L1,L2), где Q – текущее состояние автомата (q или b), i – положение считывающей головки во входной цепочке (1 < i £ n+1), L1 и L2 – содержимое стеков. Начальным состоянием алгоритма является (q,1,S, e), где S – целевой символ грамматики. Алгоритм начинает работу с начального состояния и циклически выполняет 6 шагов до тех пор, пока не перейдёт в конечное состояние или не обнаружит ошибку. Алгоритм выполняет циклически следующие шаги: Шаг 1 («Разрастание»):(q, i, Ab, m) ® (q, i, g1b, mA1), где bÎ(VNÈVT)*, m – содержимое стека возвратов L2, если A ® g1 – первая из всех альтернатив для символа A (заменяем нетерминал в стеке МПА по правилу вывода, а в стек возврата записываем выбранную альтернативу). Шаг 2 («Успешное сравнение»): (q, i, ab, m) ® (q, i+1, b, ma), если a = ai, aÎVT (текущий символ стека МПА совпадает с i-м во входной цепочке – тогда переписываем этот терминальный символ a в стек возвратов и переходим к рассмотрению следующего (i+1) символа). Шаг 3 («Завершение»): Если в стеке МПА пусто, то: (q, i, e, m) ® (b, i, e, m), если i ¹ n+1, и разбор завершён, если i =n+1. Шаг 4 («Неуспешное сравнение»): (q, i, ab, m) ® (b, i, ab, m), если a ¹ ai, aÎVT (текущий символ стека МПА отличен от i-го во входной цепочке – тогда переходим в состояние возврата). Шаг 5 («Возврат по входу»): (b, i, b, ma) ® (b, i–1, ab, m) "aÎVT (возвращаемся к предыдущему символу входной цепочки, переписав терминальный символ из стека возврата в стек МПА). Шаг 6 («Другая альтернатива»): Состояние алгоритма (b, i, gjb, mAj). § Если существует другая альтернатива для символа AÎVN: A ® gj+1, то перейти (b, i, gjb, mAj) ® (q, i, gj+1b, mAj+1) (переходим к рассмотрению другой альтернативы для последнего примененного правила для нетерминала A – записываем номер очередной альтернативы в стек возврата вместо предыдущего и заменяем цепочку в стеке). § Если A º S, i = 1 и нет больше неиспользованных альтернатив для символа S, то сигнализировать об ошибке и прекратить выполнение. § Если нет больше неиспользованных альтернатив для символа A, но A ¹ S, то перейти (b, i, gjb, mAj) ® (, i, Ab, m) (возвращаем последний нетерминал из стека возврата в стек МПА, заменив им выведенную ранее из него цепочку). В случае успешного завершения алгоритма на основе содержимого стека возврата можно построить цепочку вывода. Если в стеке содержится символ Aj, то в цепочку вывода помещают номер правила, соответствующего альтернативе A ® gj; при этом игнорируются все терминальные символы, находящиеся в стеке возврата. Заметим, что в состоянии прямого хода алгоритма (q) его поведение на очередном шаге определяется содержимым стека L1, а в состоянии обратного хода (b) – содержимым стека L2. Пример. Рассмотрим грамматику G ({+,–,/,*,a,b,(,)}, {S, R, T, F, E}, P, S), где правила P имеют вид: S ® T [ S 1 ] ½TR [ S 2 ], R ® +T [ R 1 ] ½–T [ R 2 ] ½+TR [ R 3 ] ½–TR [ R 4 ]. T ® E [ T 1 ] ½EF [ T 2 ], F ® *E [ F 1 ] ½/E [ F 2 ] ½*EF [ F 3 ] ½/EF [ F 4 ]. E ® (S) [ E 1 ] ½a [ E 2 ] ½b [ E 3 ]. Здесь каждое правило сопровождается соответствующим символом [ Ai ], который будет заноситься в стек возврата. Это нелеворекурсивная грамматика для арифметических выражений, которая была построена ранее. Рассмотрим процесс выполнения разбора цепочки a/(a–b). Состояния алгоритма будем записывать в фигурных скобках. Подчеркиваем одной чертой символы, с которыми работаем в настоящий момент; двумя чертами – не совпавший терминальный символ. В круглых скобках возле знака выводимости записываем номер соответствующего шага алгоритма.
В стеке возврата цепочка S1T2E2aF2/E1(S2T1E2aR2–T1E3b. Удалив терминальные символы, получим S1T2E2F2E1S2T1E2R2T1E3. Тогда цепочка вывода будет иметь вид: SÞTÞEFÞaFÞa/EÞa/(S)Þa/(TR)Þa/(ER)Þa/(aR)Þa/(a–T)Þa/(a–E)Þa/(a–b). Дерево вывода показано на рисунке справа. Из рассмотренного примера видно, что недостатком алгоритма нисходящего разбора с возвратами является большое время работы. Для разбора достаточно короткой цепочки из 7 символов потребовалось выполнить 70 шагов. Преимуществом алгоритма является его простота реализации и универсальность. Сам по себе данный алгоритм не используется в компиляторах, но его основные принципы лежат в основе многих нисходящих распознавателей, строящих левосторонние выводы и работающих без использования возвратов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.249 (0.01 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Итак, алгоритм работает с двумя стеками: L1 – стек МПА и L2 – стек возвратов, причём в цепочку стека L1 символы помещаются слева, а в цепочку стека L2 – справа.
Итак, алгоритм работает с двумя стеками: L1 – стек МПА и L2 – стек возвратов, причём в цепочку стека L1 символы помещаются слева, а в цепочку стека L2 – справа.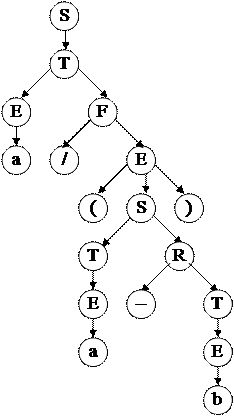 Разбор закончен, стек МПА пуст. Если взять последовательность нетерминальных символов из стека возвратов, получим цепочку номеров альтернатив и можем построить дерево вывода.
Разбор закончен, стек МПА пуст. Если взять последовательность нетерминальных символов из стека возвратов, получим цепочку номеров альтернатив и можем построить дерево вывода.


