
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Логические основы цифровой техникиСодержание книги
Поиск на нашем сайте СХЕМОТЕХНИКА ЦИФРОВЫХ ЭЛЕКТРОННЫХ УСТРОЙСТВ
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Магнитогорск, 2011 УДК
Рецензенты: д октор технических наук, профессор, заведующий кафедрой электроники и микроэлектроники ГОУ ВПО “Магнитогорский государственный технический университет им. Г.И. Носова” И.А. Селиванов; кандидат технических наук, начальник центральной электротехнической лаборатории ОАО “Магнитогорский металлургический комбинат” В.В. Головин
Авторы: Малахов О.С., Радионов А.А.
Малахов О.С., Радионов А.А. Схемотехника цифровых электронных устройств: Учебное пособие. – Магнитогорск: ГОУ ВПО “МГТУ”, 2011. – 141 с.
Рассмотрены логические и арифметические основы построения цифровой электронной техники. Представлено устройство базовых логических элементов, реализованных по различным технологиям. Приведены логические схемы и особенности функционирования наиболее распространенных цифровых комбинационных и последовательностных устройств. Изложены основные принципы построения цифро-аналоговых и аналого-цифровых преобразователей. Приведено общее представление об организации центрального процессора микро-ЭВМ. Даны сведения об индикаторных приборах, используемых для визуализации информации в устройствах цифровой электроники и сенсорных экранах. Учебное пособие предназначено для студентов высших учебных заведений, обучающихся по направлению “Электротехника, электромеханика и электротехнологии” и по специальности “Электропривод и автоматика промышленных установок и технологических комплексов”. Может быть полезно для студентов других технических направлений, интересующихся устройством элементов цифровой электроники.
УДК
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ Предлагаемое вниманию читателей учебное пособие представляет собой конспект лекций, разработанный в соответствии с Государственными образовательными стандартами Российской Федерации направления подготовки бакалавров 140600 – Электротехника, электромеханика и электротехнологии и специальности 140604 – Электропривод и автоматика промышленных установок и технологических комплексов. Материал учебного пособия разбит на введение и девять глав. В первой и во второй главах рассмотрены логические и арифметические основы построения цифровой электронной техники: логические функции и элементы, системы счисления и операции двоичной арифметики. В третьей главе приведено описание базовых логических элементов И-НЕ и ИЛИ-НЕ, реализованных по наиболее распространенным в микросхемотехнике технологиям – транзисторно-транзисторной, эмиттерно-связанной транзисторной логики и на основе комплиментарных МОП транзисторов. Четвертая глава посвящена рассмотрению цифровых устройств. Подробно рассмотрены логические схемы и особенности функционирования цифровых комбинационных (мультиплексоры и демультиплексоры, дешифраторы и шифраторы, полусумматоры, сумматоры, вычитатели и умножители, схемы контроля четности, компараторы) и последовательностных (триггеры, регистры, счетчики) электронных устройств. В пятой главе описаны цифровые импульсные устройства – одновибраторы и мультивибраторы. В шестой главе изложены основные принципы построения цифро-аналоговых и аналого-цифровых преобразователей, позволяющих создавать комбинированные схемы, в которых информация обрабатывается как в аналоговой, так и дискретной формах. Седьмая глава посвящена рассмотрению вопросов организации центрального процессора микро-ЭВМ. Рассмотрены основные элементы ЭВМ, даны общие сведения об ее устройстве и работе. В восьмой главе приведены сведения об индикаторных приборах, используемых для визуализации информации в устройствах цифровой электроники, а в девятой – об сенсорных экранах, используемых для организации диалогового режима работы микропроцессорных устройств с человеком. Вопросы курса изложены с учетом наличия знаний у студентов дисциплин “Теоретические основы электротехники” и “Физические основы электроники” в объеме, предусмотренном требованиями Государственного образовательного стандарта. Лекции не содержат ссылок на литературу, однако все литературные источники, которые авторы использовали при написании пособия, приведены в конце книги. Поэтому при возникновении каких-либо вопросов в процессе изучения курса студентам необходимо пользоваться указанной литературой. Авторы надеются, что настоящее учебное пособие окажет достойную помощь студентам при изучении соответствующего курса, а также будет полезно в их дальнейшей профессиональной деятельности. Понимая, что материал пособия может быть изложен в более доступной форме, авторы с благодарностью примут все замечания по его содержанию, которые следует направлять по адресу: 455000, г. Магнитогорск, пр. Ленина, 38, МГТУ, кафедра “Автоматизированного электропривода и мехатроники”, или на e-mail: RadionovAA@rambler.ru. ВВЕДЕНИЕ Электроника имеет короткую, но богатую событиями историю. Период ее зарождения может быть связан с появлением на рубеже XIX и XX веков простейших приемо-передатчиков ключевого (релейного) действия, с помощью которых удавалось передавать информацию на небольшие расстояния. С тех пор электроника непрерывно развивалась как по пути совершенствования компонентов, так и по пути совершенствования схемных решений электронных устройств. Элементная база электроники прошла несколько этапов развития: от радиоламп до микропроцессоров. Бурное развитие промышленной электроники началось в начале ХХ века, когда создание разнообразных типов электровакуумных приборов предопределило развитие радиосвязи, телевидения, измерительной техники. Эти успехи позволили в то время широко внедрять электронные приборы и устройства в промышленность. Однако для построения сложных электронных устройств требовалось большое количество радиоламп, что сильно сокращало время их безотказной работы. Так, при сроке службы одной лампы около 500 часов, устройство, состоящее из 2000 ламп, могло безотказно проработать не более 15 минут. Указанные недостатки электронных ламп были преодолены созданием электронных приборов с новым принципом действия, основанных на использовании свойств полупроводников (диоды, транзисторы, тиристоры и т.д.). Применение полупроводниковых приборов в промышленной электронике определялось такими их достоинствами, как долговечность, высокий к.п.д., небольшие габариты и масса. Дальнейшая растущая сложность схем потребовала развития технологии создания их элементов. В 1958 году двое ученых, живущих в совершенно разных местах, изобрели практически идентичную модель интегральной схемы. Один из них, Джек Килби, работал на Texas Instruments, другой, Роберт Нойс, был одним из основателей небольшой компании по производству полупроводников Fairchild Semiconductor. Обоих объединил вопрос: “Как в минимум места вместить максимум компонентов?”. Транзисторы, резисторы, конденсаторы и другие детали в то время размещались на платах отдельно, и ученые решили попробовать их объединить на одном монолитном кристалле из полупроводникового материала. Только Килби воспользовался германием, а Нойс предпочел кремний. В 1959 году они независимо друг от друга получили патенты на свои изобретения – началось противостояние двух компаний, которое закончилось мирным договором и созданием совместной лицензии на производство чипов. После того как в 1961 году Fairchild Semiconductor Corporation пустила интегральные схемы в свободную продажу, их сразу стали использовать в устройствах цифровой электроники – в калькуляторах и компьютерах вместо отдельных транзисторов, что позволило значительно уменьшить размер и увеличить производительность. Так появились интегральные схемы, объединяющие некоторое количество элементов на одном кристалле, т.е. позволяющие исключать внешние соединения между отдельными элементами. Сегодняшний этап развития электроники характеризуется появлением интегральных микросхем большой степени интеграции (свыше 1 миллиарда элементов на кристалле). В последние десятилетия возникло и быстро развивается новое направление электроники – цифровая обработка сигналов. Цифровые методы, основывающиеся на использовании микропроцессоров, проникли и в область электропривода. С помощью программных методов получены такие результаты, которые ранее были достижимы только сложными аппаратными средствами.
Логические функции Логические (Булевы) функции Рассмотрим функции одной переменной y = f(x). Пронумеруем эти функции (их четыре) и расположим в виде таблицы:
Видно, что f0(х) = 0, a f3(х) = 1, т.е. эти две функции не зависят от х, f1(х) = х, т.е. она не меняет аргумента. Функция f2(х) действительно содержательная функция. Она принимает значения, противоположные значениям аргумента, обозначается Рассмотрим функции двух переменных y = f(x1, x 2). Число этих функций равно 24 = 16. Пронумеруем и расположим их в естественном порядке.
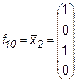
Рассмотрим более подробно эти функции. Две из них f0 = 0 и f15 = 1 являются константами. Функции
являются по существу функциями одной переменной. Наиболее важные функции двух переменных имеют специальные названия и обозначения. Заметим, что эти обозначения не всегда общеприняты. Перечислим семь важнейших функций. 1. Конъюнкция (функция И)
Конъюнкция (логическое умножение) переменных x1 и х2 равна лог. 1 в том случае, когда и x1 и х2 равны лог. 1 (отсюда и возникло название операции логическое И). Конъюнкция – это фактически обычное умножение (нулей и единиц). Иногда эту функцию обозначают x1 & x 2 или x1 2. Дизъюнкция (функция ИЛИ)
Дизъюнкци я (логическое сложение) переменных x1 и х2 равна лог. 1, если или x1 или х2 равна лог. 1 (отсюда название операции логическое ИЛИ). В тех случаях, когда число переменных больше двух, их конъюнкция равна лог. 1 при равенстве лог. 1 всех переменных; дизъюнкция равняется лог. 1, если хотя бы одна из переменных имеет значение лог. 1. 3. Импликация (следование)
Иногда импликацию обозначают x1 כ х2 или x1 → х2 (читается “из x1 следует х2 ”). Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если x1 = 0 (т. е. x1 “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если х2 = 1(т.е. х2 “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию. 4. Сложение по модулю 2, Исключающее ИЛИ (здесь и далее, если не оговорено противное, знаком “+” мы будем обозначать такое сложение):
5. Эквивалентность или подобие ~
Эта f9 = 1 тогда и только тогда, когда х1 = х2. 6. Штрих Шеффера
Иногда эту функцию называют “ НЕ И ” (так как она равна отрицанию конъюнкции). 7. Стрелка Пирса (иногда эту функцию называют штрих Лукасевича)
Эта функция является отрицанием дизъюнкции, и поэтому иногда ее называют “не ИЛИ”. Заметим, что свойства последних двух функций похожи между собой и, может быть, поэтому в литературе их часто путают (т. е. называют f8 штрихом Шеффера, а f14 – стрелкой Пирса). Три оставшиеся функции, (f2, f4 и f11) особого значения в дискретной математике не имеют. Операцию отрицания называют инверсией или дополнением. Для ее обозначения используют черту над соответствующим выражением. Операция определяется следующими постулатами: если х = 1, то В математике установлен определенный порядок выполнения операций в сложном выражении. Подобно этому в сложном логическом выражении вначале выполняются операции инверсии, затем операции конъюнкции и в последнюю очередь операции дизъюнкции. Теоремы булевой алгебры отражают связи, существующие между операциями, выполняемыми над логическими переменными. Сформулируем наиболее важные из них: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. Справедливость всех перечисленных теорем может быть до-казана непосредственной подстановкой.
1.1.3. Способы задания логических функций В классической математике для задания функции обычно используются два способа: аналитический (запись формулой) и табличный (таблицами значений функций). Для описания функций алгебры логики могут быть использованы различные способы. Основными из них являются описание функций в словесной форме, в виде таблиц истинности и алгебраических выражений. Проиллюстрируем словесное описание функции алгебры логики на примере. Логическая функция трех переменных равна 1, если хотя бы две входные переменные равны 1. Данный вид описания наиболее часто применяется для первоначального, исходного описания поведения логического устройства. Таблица, содержащая все возможные комбинации входных переменных xn-1 …x1x0 и соответствующие им значения выходных переменных y i, называется таблицей истинности или комбинационной таблицей. В общем случае таблица истинности содержит 2n строк и m+n столбцов, где n – количество входных сигналов, а m – выходных. При описании функций алгебры логики алгебраическим выражением используются две стандартные формы ее представления – так называемые дизъюнктивная и конъюнктивная нормальные формы. Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входит один раз. ДНФ может быть получена из таблицы истинности с использованием следующего алгоритма: а) для каждого набора переменных, на котором функция алгебры логики равна единице, записывают элементарные логические произведения входных переменных, причем переменные, равные нулю, записывают с инверсией. Полученные произведения называют конституентами единицы; б) логически суммируют все конституенты единицы. ДНФ, полученную суммированием конституент единицы, называют совершенной (СДНФ). Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его инверсия входят один раз. КНФ может быть получена из таблицы истинности с использованием следующего алгоритма: а) для каждого набора переменных, на котором функция алгебры логики равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентами нуля; б) логически перемножают все полученные конституенты нуля. КНФ, полученную суммированием конституент нуля, также называют совершенной (СКНФ). Пример 1.1. Запишите дизъюнктивную и конъюнктивную нормальные формы для следующей таблицы истинности:
Решение. Согласно приведенному выше алгоритму дизъюнктивная нормальная форма примет вид
а конъюнктивная нормальная форма определится как
Иногда удобнее применять не саму функцию алгебры логики, а ее инверсию. В этом случае при использовании вышеописанных методик для записи СДНФ необходимо выбирать нулевые, а для записи СКНФ – единичные значения функции.
Логические элементы Функция алгебры логики однозначно определяет внутреннюю структуру логического устройства. С помощью элементарных узлов, реализующих основные логические операции, можно построить логическую схему, выполняющую заданный алгоритм преобразования исходных логических переменных. В соответствии с перечнем логических операций различают три основных логических элемента: И, ИЛИ, НЕ. Условные графические обозначения этих логических элементов показаны на рис. 1.1.
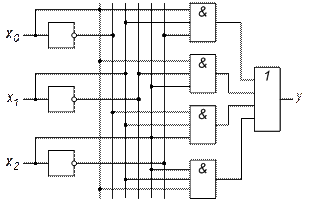
Рис. 1.1. Условные графические обозначения основных (а) и совмещающих в себе две функции (б) логических элементов Число входов логических элементов И или ИЛИ может быть произвольным. Элемент НЕ всегда имеет только один вход. Для построения логической схемы необходимо логические элементы, предназначенные для выполнения логических операций, указанных в функции алгебры логики, располагать от входа в порядке, определенном булевым выражением. Пример 1.2. Построить структурную схему логического устройства по функции алгебры логики (1.1). Решение приведено на рис. 1.2
Рис. 1.2. Пример структурной схемы логического устройства
Функционально полной системой называется совокупность логических элементов, позволяющая реализовать логическую схему произвольной сложности. На практике широкое применение нашли логические элементы, совмещающие в себе функции логического сложения и отрицания (ИЛИ-НЕ), а также логического умножения и отрицания (И-НЕ).
Системы счисления Для представления в цифровых устройствах чисел, а также другой информации наряду с привычной для нас десятичной системой счисления широко используются другие системы. Существующие системы счисления подразделяются на позиционные и непозиционные. В непозиционных системах значение конкретной цифры постоянно и не зависит от ее расположения в записи числа. Примером такой системы счисления является Римская система записи числа. Например, в числе XXXVII значение цифры Х не зависит от ее местоположения в записи числа. Оно везде равно 10. В позиционных системах счисления значимость конкретной цифры определяется ее местоположением в записи числа. Числа в таких системах счисления представляются последовательностью цифр (цифр разрядов), разделенных запятой на две группы: группу разрядов, изображающую целую часть числа, и группу разрядов, изображающую дробную часть числа:
Здесь a0, a1, … обозначают цифры нулевого, первого и т.д. разрядов целой части числа, а-1, а-2, … – цифры первого, второго и т.д. разрядов дробной части числа. Цифре разряда приписан вес pk, где p – основание системы счисления; k – номер разряда, равный индексу при обозначении цифр разрядов. Так, приведенная выше запись (2.1) означает следующее количество:
Двоичная арифметика Основной операцией, которая используется в цифровых устройствах при различных вычислениях, является операция алгебраического сложения чисел (сложения, в котором могут участвовать как положительные, так и отрицательные числа). Вычитание легко сводится к сложению путем изменения на обратный знака вычитаемого. Операции умножения и деления также выполняются с помощью операции сложения и некоторых логических действий.
Дополнительного кода При записи кода числа знак числа представляется цифрами 0 (для положительных чисел) и 1 (для отрицательных чисел). Для пояснения сущности излагаемого ниже метода сложения рассмотрим следующий пример. Пусть требуется сложить два десятичных числа 0 83110 и 1 37610. Так как второе слагаемое – отрицательное число, пользование обычным приемом вычитания потребовало бы последовательности действий с займами из старших разрядов. Предусматривать в цифровом устройстве дополнительно такую последовательность действий не обязательно. Достаточно отрицательное число 1 37610 предварительно преобразовать в так называемый дополнительный код следующим образом: во всех разрядах, кроме знакового, запишем дополнение до 9 к цифрам этих разрядов и затем прибавим 1 в младший разряд. Число 1 376 в дополнительном коде есть 1 624. Далее произведем сложение по правилам сложения с передачей переносов в старшие разряды (т.е. так, как складываются положительные числа). При сложении складываются и двоичные цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса:
В двоичной системе счисления дополнительный код отрицательного числа формируется по следующему правилу: инвертируются (путем замены 0 на 1 и 1 на 0) цифры всех разрядов, кроме знакового, и в младший разряд прибавляется 1. Например, дополнительный код числа 1 101102 выглядит как 1 010102. Обратное преобразование из дополнительного кода в прямой код производится по тому же правилу.
Пример 2.1. Сложить положительное число 0 101102 и отрицательное число 1 011012. Решение. Дополнительный код числа 1 011012 составит 1 10011, тогда сложение будет иметь вид
Как указывалось выше, перенос, возникающий из знакового разряда, отбрасывается. Если результат сложения есть отрицательное число, то оно оказывается в дополнительном коде.
Контрольные вопросы и задания 1. Объясните разницу позиционной и непозиционной системами счисления. Приведите примеры таких систем. 2. В чем заключается суть кодирования числа в позиционных системах счисления. Дайте объяснение понятия основание системы. 3. Какие цифры используются в двоичной, десятичной и шестнадцатеричной системах счисления? 4. Какие правила перевода чисел из одной позиционной системы счисления в другую Вы знаете? Переведите число 3F16 в двоичную и десятичную системы счисления. Переведите число 25610 в двоичную и шестнадцатеричную системы счисления. Переведите число 110100112 в десятичную и шестнадцатеричную системы счисления. 5. Поясните правила сложения положительных двоичных чисел. Сложите числа 1011 01012 и 0101 01112. 6. Что такое дополнительный код числа? Поясните правила сложения с отрицательным числом. Переведите числа 6510 и -3110 в двоичный код и сложите их.
Диодно-транзисторная логика
Наиболее простой логический элемент получается при помощи диодов. Схема такого элемента приведена на рис. 3.1. В этой схеме при подаче нулевого потенциала на любой из входов (или на оба сразу) через резистор будет протекать ток и на его сопротивлении возникнет падение напряжения. В результате на выходе схемы будет единичный потенциал, только если подать единичный потенциал сразу на оба входа микросхемы. То есть схема реализует функцию "2И".
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

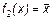 и называется отрицанием.
и называется отрицанием.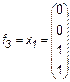 ,
, 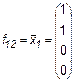 ,
, 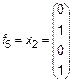 ,
, 
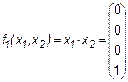 .
.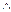 x 2.
x 2.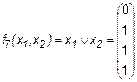 .
.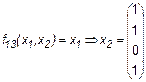 .
.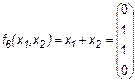 .
.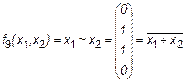 .
.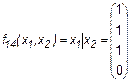 .
.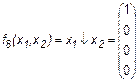 .
.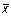 = 0, если х = 0, то
= 0, если х = 0, то 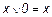 ;
;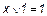 ;
;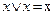 ;
;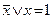 ;
;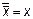 ;
;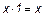 ;
;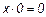 ;
;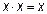 ;
;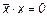 ;
;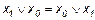 ;
;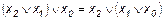 ;
;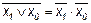 ;
;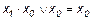 ;
;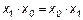 ;
;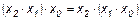 ;
;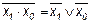 ;
;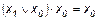 ;
;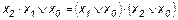 ;
;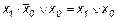 ;
;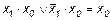
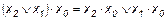 ;
;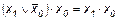 ;
;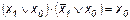
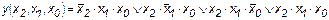 , (1.1)
, (1.1)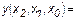
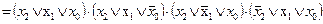 . (1.2)
. (1.2)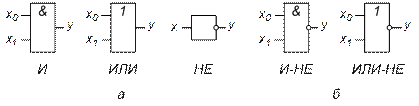
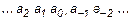 (2.1)
(2.1) . (2.2)
. (2.2)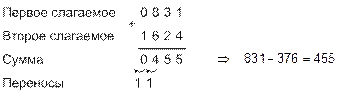
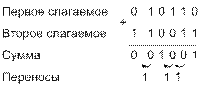
 Диодно-транзисторная логика (ДТЛ) – технология построения цифровых схем на основе биполярных транзисторов, диодов и резисторов. Свое название технология получила благодаря реализации логических функций (например, И) с помощью диодных цепей, а усиления сигнала – с помощью транзистора.
Диодно-транзисторная логика (ДТЛ) – технология построения цифровых схем на основе биполярных транзисторов, диодов и резисторов. Свое название технология получила благодаря реализации логических функций (например, И) с помощью диодных цепей, а усиления сигнала – с помощью транзистора.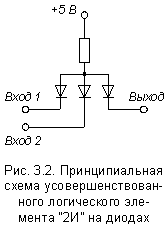 Приведенная схема обладает таким недостатком, как смещение логических уровней на выходе микросхемы. Напряжение нуля и напряжение единицы на выходе схемы выше входных уровней на 0,7 В. Это вызвано падением напряжения на входных диодах. Скомпенсировать эт
Приведенная схема обладает таким недостатком, как смещение логических уровней на выходе микросхемы. Напряжение нуля и напряжение единицы на выходе схемы выше входных уровней на 0,7 В. Это вызвано падением напряжения на входных диодах. Скомпенсировать эт


