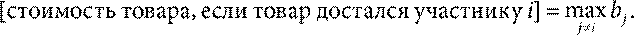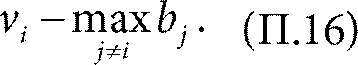Доказательство совместимости по стимулам аукциона второй цены

 

Рассмотрим аукцион второй цены, на котором один товар разыгрывается между n участниками. Обозначим v_i истинную ценность товара для участника i (от английского слова value – ценность). Далее обозначим через b_i ставку участника i (от англ. bid – ставка). Эти обозначения будем использовать для любого i = 1,2, …, n.

Совместимость по стимулам означает, что верна следующая теорема.

Теорема (Викри). Участник i получает максимальную прибыль, если b_i = v_i.

Доказательство. Если участник i получает товар, следовательно, его ставка b_i была самой высокой. Поскольку мы имеем дело с аукционом второй цены, то стоимость товара равна самой высокой из оставшихся ставок:

 

 

При этом ценность товара для участника i равна v_i. Значит, если участник i получает товар, то его прибыль составит

 

 

Если участник i товар не получает, он не приобретает никакой ценности и ничего не платит, то есть его прибыль равна нулю.

Дальше доказательство ведется так же, как в разделе «Результат Викри» в главе 8, и в качестве иллюстрации мы можем по‑прежнему использовать рис. 8.2 и рис. 8.3. Допустим, что ставки всех участников, кроме i, фиксированы. Мы покажем, что при правдивой ставке b_i = v_i прибыль участника i та же или больше, чем при повышенной ставке b_i > v_i или пониженной b_i < v_i. Подчеркнем, что это утверждение верно при любых (фиксированных) ставках других участников.

Предположим, что b_i > v_i. Рассмотрим три случая относительно ставок b _j, j ≠ i.

1. Допустим, что b_i – самая высокая ставка и, кроме того, все остальные участники поставили меньше, чем v_i (рис. 8.2 вверху). Тогда товар по‑прежнему достается участнику i по стоимости max _{j ≠ i} b_j, и участник i получает точно такую же прибыль (П.16), что и при правдивой ставке v_i.

2. Теперь предположим, что другой участник k сделал ставку b_k > b_i (см. рис. 8.2 в середине). Тогда участник i товар не получает, его прибыль равна нулю. Но поскольку b_i > v_i, то и при честной ставке v_i участник i тоже не получил бы товар. Значит, в этом случае прибыль участника i при честной ставке тоже равна нулю.

3. Наконец, допустим, что b_i – самая высокая ставка и v_i < max _{j ≠ i} b_j < b_i (см. рис. 8.2 внизу). Так как v_i < b_i, такая ситуация возможна. Она возникает, когда самая высокая ставка других участников выше v_i, но ниже b_i. Если бы i поставил v_i, то i не получил бы товар, прибыль была бы равна нулю. Но теперь b_i – самая высокая ставка, поэтому товар достается i. Прибыль i по‑прежнему вычисляется по формуле (П.16), но только прибыль становится отрицательной, поскольку ценность товара меньше его стоимости. Значит, в этом случае прибыль i меньше, чем при честной ставке.

Во всех трех случаях 1–3 участник i не получил прибыль выше, чем при честной ставке v_i.

Теперь предположим, что b_i < v_i, то есть ставка занижает реальную ценность. Опять рассмотрим три случая относительно ставок других участников b_j, j ≠ i.

1ʹ. Допустим, b_i – самая высокая ставка (рис. 8.3 вверху). Тогда товар по‑прежнему достается участнику i по стоимости max _{j ≠ i} b_j. В этом случае прибыль участника i та же, что и прежде (П.16). Она в точности такая же, как и при честной ставке v_i.

2ʹ. Теперь предположим, что другой участник l сделал ставку b_l > v_i (рис. 8.3 в середине). В этом случае при честной ставке v_i участник i товар не получает.

Но тогда и при заниженной ставке b_i < v_i участник i не получит товар. Значит, прибыль i равна нулю и при честной, и при заниженной ставке.

3ʹ. Наконец, допустим, что b_i < max _{j ≠ i} b_j < v_i (рис. 8.3 внизу). Так как b_i < v_i такая ситуация возможна. Она возникает, когда самая высокая ставка других участников выше b_i, но ниже v_i. Тогда при честной ставке товар достался бы участнику i, и его прибыль, по формуле (П.16), была бы положительной. Но поскольку b_i теперь не самая высокая ставка, товар достанется другому участнику и прибыль участника i равна нулю. Значит, в этом случае прибыль i меньше, чем при честной ставке.

Во всех трех случаях 1ʹ–3ʹ участник i не получил более высокую прибыль, чем при честной ставке v_i.

В результате делаем вывод, что и при заниженной, и при завышенной ставке участник i получает не больше, чем при честной ставке b_i = v_i. Таким образом, мы доказали, что в аукционе второй цены выгоднее всего делать честную ставку.

Назад к Главе 8

 

Благодарности

 

Мы благодарим издательство «Манн, Иванов и Фербер» и его директора Артема Степанова за возможность опубликовать эту рукопись. Большое спасибо Ренату Шагабутдинову за быструю и позитивную обратную связь. Мы хотим выразить признательность ответственному редактору Наталье Шульпиной за помощь в подготовке книги к изданию. Благодаря высокому профессионализму Натальи наша совместная работа была творческой и приятной. Мы также благодарим всех сотрудников издательства, которые участвовали в создании книги.

Мы искренне признательны коллегам со всего мира за энтузиазм и поддержку этого проекта. Спасибо вам, Сергей Измалков, Алексей Герасимов, Александр Веремьев, Даниил Мусатов, Алексей Савватеев, Джерард Пост, Себастьяно Винья, Питер‑Тьерк де Бур, Мор Харкол‑Балтер, Роберт Ерра, Франк Тайсман, Кавита Раманан, Фэн Чжун, Сара ван де Гейр, Александр Схрейвер, Ярослав Кристул, Нардо Боргман, Мартье ван де Врухт, за материалы, интервью и экспертные отзывы, которые нам были нужны для каждой главы. Особая благодарность Константину Авраченкову за экспертные комментарии ко всей рукописи, сделанные им в ходе проекта, и Роберту Фицнеру за иллюстрации к главе 4.

 

Нелли

Это был большой и сложный проект. Список людей, принявших в нем участие, очень длинный, и я все равно не сумею назвать всех.

Прежде всего хочу выразить признательность Андрею за сотрудничество. Мне было интересно и комфортно с ним работать, я не уставала удивляться глубине и разнообразию его знаний. Спасибо, Андрей, что взялись со мной за этот проект!

Моя семья стала узким кругом наших первых читателей. Мой дедушка, замечательный физик и энтузиаст науки Виталий Анатольевич Зверев (ему 92 года!), читал все главы в день их появления. Я с нетерпением ждала его развернутых комментариев, которые подсказали нам много идей; например, именно из этих комментариев возник раздел о кодировании цветов в главе 3. Спасибо, деда Витя, ты неподражаемый пример настоящего ученого! Мой брат Петр Антонец – гуманитарий с искренним интересом к науке и технике – стал для меня «эталонным» читателем. Мы исправили все, что ему было непонятно! Спасибо моей маме Нине Зверевой, папе Владимиру Антонцу и сестре Катерине Петелиной за быстрые, оригинальные и неизменно позитивные отзывы о каждой главе. Особое спасибо маме за то, что несколько лет назад подтолкнула меня к писательству и оказывала постоянную вдохновляющую поддержку моей писательской карьеры.

Мы получили необыкновенную поддержку от широкого круга друзей, коллег и потенциальных читателей. Кроме уже перечисленных выше имен, попробую назвать тех, чей энтузиазм, идеи, цитаты и комментарии нашли отражение на этих страницах: Марк Хацернов, Людмила Остроумова‑Прохоренкова, Нина Петелина, Татьяна Петелина, Диана Кобленкова, Михаил Федоткин, Наум Шимкин, Нико ван Дайк, Эрвин Ханс, Пим ван дер Хорн, Мартен ван Стейн, Марк Утц, Ян‑Виллем Полдерман, Ричард Бушери, Ингеборг Бликкер и многие другие. Огромное спасибо!

Спасибо моей взрослой дочери Наталии Литвак, прекрасной подруге и специалисту по инновациям. Из наших разговоров я почерпнула много интересных идей о роли науки в практике. Спасибо моей дочке Пиали за веселый характер и искренний интерес к моему писательству. Надеюсь, когда‑нибудь ты сможешь это прочитать! Спасибо моему мужу Пранабу за бесконечное тепло, понимание и терпение.

 

Андрей

Мне был очень интересен этот проект, поэтому, несмотря на жуткий постоянный цейтнот, я сделал все, чтобы посвятить ему достаточно времени. Я очень благодарен Нелли за то, что она меня втянула во все это.:‑)

 

Об авторах

 

Нелли Литвак – профессор математики, преподаватель в Университете Твенте (Нидерланды), автор более 60 научных работ и книг. Мать двух дочерей.

 

Андрей Райгородский – федеральный профессор математики, автор более 150 научных статей, 20 книг и 10 онлайн‑курсов. Директор физтех‑школы прикладной математики и информатики, заведующий лабораторией продвинутой комбинаторики и сетевых приложений МФТИ, заведующий кафедрой дискретной математики МФТИ, руководитель исследовательской группы компании «Яндекс».

 

Эту книгу хорошо дополняют:

1. Удовольствие от x. Стивен Строгац

2. Голая статистика. Чарльз Уилан

3. Теория игр. Авинаш Диксит, Барри Нейлбафф

4. Как не ошибаться. Джордан Элленберг

[1] Мы включили в книгу приложения для подготовленного читателя, чтобы ее можно было использовать в качестве учебника, например для спецкурса в старших классах или для вводных лекций в вузе.

 

[2] Отсылка к знаменитому одноименному роману лауреата Нобелевской премии Германа Гессе. Прим. ред.

 

1

 Holt Charles С. Learning how to plan production, inventories, and work force // Operations Research, 50(l):96–99, 2002.

 

2

 Канторович Л. В. Об одном эффективном методе решения некоторых классов экстремальных проблем // Докл. АН СССР. 1940. Том 28. С. 212–215.

 

[3] В приложении 2 к главе 2 для подготовленного читателя мы более подробно рассматриваем еще один маленький пример составления расписаний.

 

[4] В приложении 3 к главе 2 мы объясняем для заинтересованного читателя основные идеи этого метода более подробно. Заметим, что это объяснение не требует математической подготовки.

 

3

 Bixby E. Robert. A brief history of linear and mixed‑integer programming computation. Documenta Mathematica, p. 107–121, 2012.

 

4

 Kroon Leo, Huisman Dennis, Abbink Erwin, Fioole Pieter‑Jan, Fischetti Matteo, Maroti Gabor, Schrijver Alexander, Steenbeek Adri and Ybema Roelof. The new dutch timetable: The or revolution // Interfaces, 39(1):6–17, 2009.

 

[5] Для интересующихся читателей в приложении 1 к главе 3 мы приводим вычисления числа последовательностей из нулей и единиц заданной длины.

 

5

 Shannon Claude Elwood. A mathematical theory of communication // The Bell System technical Journal, 27:379–423, 623–656, 1949.

 

[6] Для подготовленного читателя в приложении 2 к главе 3 приведена точная формула границы Хэмминга и ее доказательство в общем случае.

 

6

 Слоэн Н. Дж. А., Мак‑Вильямс Ф. Дж. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.

 

7

 Спенсер Дж., Алон Н. Вероятностный метод. М.: Бином. Лаборатория знаний, 2007.

 

8

 Keevash Peter. The existence of designs // arXiv preprint arXiv.H01.3665, 2014.

 

[7] Такой остров действительно есть, его население составляет 4,5 тысяч человек; кенгуру там гораздо больше!

 

[8] В приложении 1 к главе 4 для подготовленного читателя приведены формулы, которыми мы воспользовались при подготовке в табл. 4.1, в общем виде.

9  Renyi A. and Erdos P. On random graphs // Publicationes Mathematicae, 6(290–297):5, 1959.

10  Erdos Paul and Renyi Alfred. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci, 5:17–61, 1960.

[9] В приложениях для подготовленного читателя мы будем придерживаться математической терминологии: «вершины» и «ребра».

 

[10] В приложении 2 к главе 4 мы приводим математическую формулировку теоремы Эрдеша – Реньи о фазовом переходе.

 

[11] В приложении 3 к главе 4 мы приводим идею доказательства результата Эрдеша – Реньи в более точной математической формулировке. Подробно это доказательство рассматривается в книге Андрея «Модели случайных графов» (Райгородский A. M. Модели случайных графов. 2‑е изд. М.: МЦНМО, 2016.).

 

11

 Albert Reka, Jeong Hawoong and Barabasi Albert‑Laszlo. Error and attack tolerance of complex networks // Nature, 406(6794):378–382, 2000.

 

12

 Doyle J. C., Alderson D. L., Li L., Low S., Roughan M., Shalunov S., Tanaka R. and Willinger W. The «robust yet fragile» nature of the Internet. PNAS, 102(41): 14497–14502, 2005.

 

13

 Mahadevan P., Krioukov D., Fall K. and Vahdat A. Systematic topology analysis and generation using degree correlations // ACM SIGCOMM Computer Communication Review, 36(4):135–146, 2006.

 

14

 Eager Derek L., Lazowska Edward D. and Zahorjan John. Adaptive load sharing in homogeneous distributed systems. Software Engineering, IEEE Transactions on, (5): 662–675, 1986.

 

15

 Введенская Н. Д. Система обслуживания с выбором наименьшей из двух очередей – асимптотический подход / Н. Д. Введенская, Р. Л. Добрушин, Ф. И. Карпелевич // Проблемы передачи информации. – 1996. – № 32 (1). – С. 20–34.

 

16

 Richa Andrea W., Mitzenmacher M. and Sitaraman R. The power of two random choices: A survey of techniques and results // Combinatorial Optimization, 9:255–304, 2001.

 

17

 Richa Andrea W., Mitzenmacher M. and Sitaraman R. The power of two random choices: A survey of techniques and results // Combinatorial Optimization, 9:255–304, 2001.

 

[12] В приложении к главе 5 мы приводим более формальное математическое объяснение и формулы для подсчета данных, приведенных в табл. 5.1.

 

[13] Заметим, что не нужно путать шифрование и кодирование. Как мы уже рассказывали в главе 3, задачи теории кодирования состоят вовсе не в том, чтобы скрыть от кого‑либо информацию. Коды строятся прежде всего для того, чтобы обеспечить бесперебойную передачу данных, в том числе и тех, которые подвержены помехам и искажениям. А вот шифрование – это как раз «сокрытие информации от посторонних». Этим и занимается криптография.

 

[14] См. https://www.youtube.com/watch?v=G2_Q9FoD‑oQ; https://www.youtube.com/watch?v=V4V2bpZlqx8.

 

[15]  Источник: Prime Pages https://primes.utm.edu/howmany.html.

 

[16] В приложении 2 к главе 6 мы более подробно рассказываем о выборе р и g.

 

[17] В приложении 1 к главе 6 мы приводим простое доказательство, что по схеме Диффи – Хеллмана Боб и Алиса получат одно и то же число.

 

18

 Adrian David, Bhargavan Karthikeyan, Durumeric Zakir, Gaudry Pierrick, Green Matthew, et al. Imperfect forward secrecy: How diffie‑hellman fails in practice // Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, p. 5–17. ACM, 2015.

 

19

 Adrian David, Bhargavan Karthikeyan, Durumeric Zakir, Gaudry Pierrick, Green Matthew, et al. Imperfect forward secrecy: How diffie‑hellman fails in practice // Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, p. 5–17. ACM, 2015.

 

[18] https://freedom‑to‑tinker.com/blog/haldermanheninger/how‑is‑nsa‑breaking‑so‑much‑crypto/.

 

[19] http://www.cnet.com/news/crypto‑class‑bans‑foreign‑students/.

 

[20] https://www.eff.org/fr/cases/bernstein‑v‑us‑dept‑justice.

 

[21] https://www.schneier.com/blog/archives/2015/05/the_logjam_and_.html.

 

20

 Heule Stefan, Nunkesser Marc and Hall Alexander. Hyperloglog in practice: Algorithmic engineering of a state of the art cardinality estimation algorithm // Proceedings of the 16th International Conference on Extending Database Technology, pp. 683–692. ACM, 2013.

 

21

 Sketch of the day: Hyperloglog – cornerstone of a big data infrastructure. http://research.neustar.biz/2012/10/25/sketch‑of‑the‑day‑hyperloglog‑cornerstone‑of‑a‑big‑data‑infrastructure/. Accessed: 2015‑11‑22.

 

22

 Flajolet Philippe, Fusy Eric, Olivier G. and Meunier Frederic. Hyperloglog: The analysis of a near‑optimal cardinality estimation algorithm // Philippe Jacquet, editor, Analysis of Algorithms 2007 (AofA07), volume AH of Discrete Mathematics and Theoretical Computer Science Proceedings, p. 127–146, 2007.

 

[22] В приложении 1 к главе 7 объясняется, откуда возникает двойной логарифм.

 

23

 Sketch of the day: Hyperloglog – cornerstone of a big data infrastructure. http://research.neustar.biz/2012/10/25/sketch‑of‑the‑day‑hyperloglog‑cornerstone‑of‑a‑big‑data‑infrastructure/. Accessed: 2015‑11‑22.

 

24

 Heule Stefan, Nunkesser Marc and Hall Alexander. Hyperloglog in practice: Algorithmic engineering of a state of the art cardinality estimation algorithm // Proceedings of the 16th International Conference on Extending Database Technology, pp. 683–692. ACM, 2013.

 

25

 Backstrom Lars, Boldi Paolo, Rosa Marco, Ugander Johan and Vigna Sebastiano. Four degrees of separation // Proceedings of the 4th Annual ACM Web Science Conference, p. 33–42. ACM, 2012.

 

26

 Sketch of the day: Hyperloglog – cornerstone of a big data infrastructure. http://research.neustar.biz/2012/10/25/sketch‑of‑the‑day‑hyperloglog‑cornerstone‑of‑a‑big‑data‑infrastructure/. Accessed: 2015‑11‑22.

 

27

 Backstrom Lars, Boldi Paolo, Rosa Marco, Ugander Johan and Vigna Sebastiano. Four degrees of separation // Proceedings of the 4th Annual ACM Web Science Conference, p. 33–42. ACM, 2012.

 

28

 Heule Stefan, Nunkesser Marc and Hall Alexander. Hyperloglog in practice: Algorithmic engineering of a state of the art cardinality estimation algorithm // Proceedings of the 16th International Conference on Extending Database Technology, pp. 683–692. ACM, 2013.

 

29

 Sketch of the day: Hyperloglog – cornerstone of a big data infrastructure. http://research.neustar.biz/2012/10/25/sketch‑of‑the‑day‑hyperloglog‑cornerstone‑of‑a‑big‑data‑infrastructure/. Accessed: 2015‑11‑22.

 

30

 Vickrey William. Counterspeculation, auctions, and competitive sealed tenders // The Journal of finance, 16(l):8–37, 1961.

 

[23] Помимо поисковых систем аукционами второй цены пользуется корпорация электронной торговли eBay.

 

[24] В приложении к главе 8 приведено более формальное доказательство совместимости по стимулам в аукционе второй цены.

 

[25] Для читателей с математической подготовкой, которых заинтересовала теория аукционов и три Нобелевские премии, рекомендуем видеолекцию Алексея Савватеева (Савватеев А. Теория аукционов. Наиболее значимые достижения [Электронный ресурс]. – Режим доступа: https://www.youtube.com/watch?v=fCIU07zg9HQ&feature=youtu.be.), где он подробно и очень доходчиво объясняет математическую сторону вопроса.

 

31

 Easley David and Kleinberg Jon. Networks, crowds, and markets: Reasoning about a highly connected world. Cambridge University Press, 2010.

 

32

 Stokes Donald E. Pasteur’s quadrant: Basic science and technological innovation. Brookings Institution Press, 2011.

 

33

 Райгородский A. M. Модели случайных графов. 2‑е изд. М.: МЦНМО, 2016.

 

[26] На самом деле, если нужно выбрать два разных сервера, эта вероятность равна

 

но это значение очень близко к u ² _k, когда n достаточно велико.

 

34

 Введенская Н. Д. Система обслуживания с выбором наименьшей из двух очередей – асимптотический подход / Н. Д. Введенская, Р. Л. Добрушин, Ф. И. Карпелевич // Проблемы передачи информации. – 1996. – № 32 (1). – С. 20–34.

 

35

 Виноградов И. М. Основы теории чисел. М. – Ижевск: НИЦ «Регулярная и хаотическая динамика, 2003.

 

36

 Flajolet Philippe, Fusy Eric, Olivier G. and Meunier Frederic. Hyperloglog: The analysis of a near‑optimal cardinality estimation algorithm // Philippe Jacquet, editor, Analysis of Algorithms 2007 (AofA07), volume AH of Discrete Mathematics and Theoretical Computer Science Proceedings, p. 127–146, 2007.