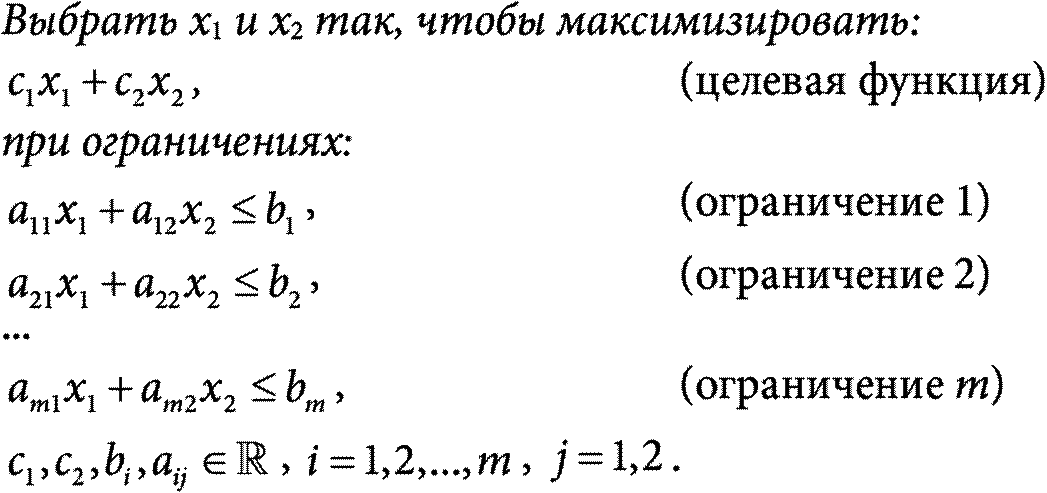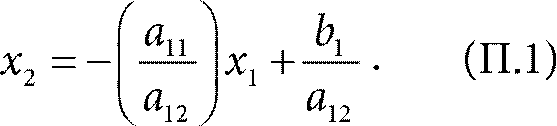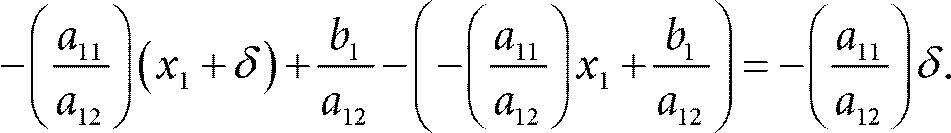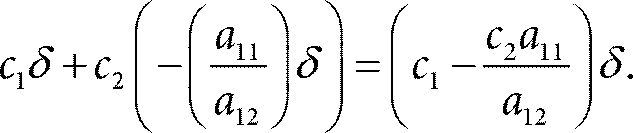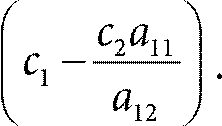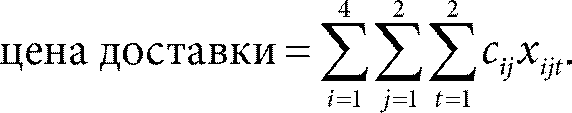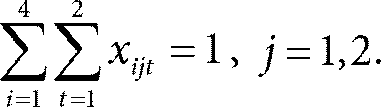Существует оптимальное решение, соответствующее одному из углов многогранника

 

Отметим, что в выражении стоимости 1020 − 2 × АЮ − 5 × БЮ в нашем примере оптимальные значения АЮ и БЮ не зависят от слагаемого 1020. Решение будет то же, если мы будем минимизировать −2 × АЮ − 5 × БЮ или максимизировать 2 × АЮ + 5 × БЮ.

Рассмотрим задачу линейного программирования с двумя переменными в общем виде.

 

 

Заметьте, что, во‑первых, задача максимизации эквивалентна задаче минимизации с коэффициентами − с ₁ и − с ₂. Во‑вторых, любое неравенство со знаком ≤ можно превратить в эквивалентное неравенство со знаком ≥, умножив обе части неравенства на –1. Поэтому задача выше, для двух переменных и m ограничений, сформулирована действительно в общем виде. Все значения коэффициентов a, b, с – произвольные действительные числа, которые могут быть как положительными, так и отрицательными.

Каждое ограничение задает полуплоскость значений, на которой оно выполняется. Если пересечение всех m полуплоскостей пусто, то допустимого решения просто не существует. Поэтому допустим, что m полуплоскостей содержат общую ограниченную область S допустимых значений. (Мы не будем рассматривать случай, когда область не ограничена.) Очевидно, что S – это многоугольник, поскольку область S ограничена прямыми.

Утверждение. Максимальное значение целевой функции достигается в одном из углов S.

Доказательство. Обозначим оптимальное решение через x ^*₁, x ^*₂. Заметьте, что x ^*₁, x ^*₂ не может быть внутренней точкой S, потому что в этом случае оба значения переменных можно либо увеличить, либо уменьшить, таким образом увеличивая значение целевой функции. Например, в нашей задаче в главе 2 решение (58,8) является внутренней точкой, поэтому не может быть оптимальным.

Значит, x ^*₁, x ^*₂ лежит на одной из сторон многоугольника S. На каждой из сторон одно из ограничений превращается в равенство. Рассмотрим сторону, которая соответствует первому ограничению: a ₁₁ x ₁ + a ₁₂ x ₂ = b ₁. Что происходит, если мы начнем двигаться вдоль этой стороны?

Не уменьшая общности, допустим, a ₁₂ ≠ 0. Для начала перепишем равенство в более привычном виде как уравнение прямой:

 

 

Допустим, мы начали в точке (x ₁, x ₂). Теперь допустим, что мы немного изменили х ₁ и получили новую координату x ₁+ δ, где δ >0 достаточно мало, чтобы все остальные ограничения, кроме первого, по‑прежнему строго выполнялись. Тогда значение х ₂ изменится на величину

 

 

При этом нетрудно проверить, что целевая функция изменится на величину

 

 

Заметьте, что это число не зависит от (x ₁, x ₂). Значит, в какой бы точке прямой (П.1) мы не начали движение, в результате перемещения по этой прямой, изменение значения целевой функции зависит только от коэффициента

 

 

Если он отрицательный, то, увеличивая x ₁ и двигаясь по прямой, мы можем только уменьшить целевую функцию. Аналогично если коэффициент положительный, то, двигаясь по прямой в сторону увеличения x ₁, мы можем целевую функцию только увеличить. Наконец, если коэффициент равен нулю, значение целевой функции на всей прямой постоянно.

Стало быть, из любой точки на данной стороне S мы можем двигаться либо в сторону уменьшения, либо в сторону увеличения x ₁ так, чтобы значение целевой функции не уменьшалось. Таким образом мы можем менять значение x ₁, пока какое‑то другое ограничение не превратится в равенство. В этом случае мы столкнулись с углом многоугольника S, в котором достигается максимальное значение целевой функции на всей рассмотренной нами стороне. Поскольку сторону мы выбрали произвольно, делаем вывод, что максимальное значение целевой функции достигается в одном из углов S и мы можем выбрать этот угол в качестве x ^*₁, x ^*₂.

Очевидно, что это доказательство легко обобщить на любое количество n переменных.

 

Пример задачи целочисленного программирования

 

Допустим, нам нужно отправить грузовики с товаром к двум разным клиентам. Всего у нас в разных точках четыре грузовика. Обозначим через cij цену отправки грузовика i =1,2,3,4 к клиенту j =1,2. На любую доставку требуется полдня. Доставку можно осуществить либо утром (первая половина дня), либо днем (вторая половина дня). Нужно решить, к какому клиенту какой грузовик поедет и в какой момент времени.

Введем переменные x_ijt, i =1,2,3,4; j =1,2; t =1,2. Эти переменные могут принимать значение 0 или 1. Например, если грузовик 3 едет к клиенту 2 в первой половине дня, то x ₃₂₁=1. Если этого не происходит (то есть грузовик 3 в первой половине дня никуда не едет или едет к другому клиенту), то x ₃₂₁=0.

В нашей небольшой задаче всего 4×2×2=16 переменных, то есть ее можно решить и вручную.

Целевая функция – это цена доставки, и вычисляется она очень просто:

 

 

Например, если грузовик 3 едет к клиенту 2 в первой половине дня, то x ₃₂₁ = 1 и мы прибавим к общей стоимости c ₃₂. А если грузовик 3 к клиенту 2 не поедет, тогда x ₃₂₁ = x ₃₂₂ = 0 и c ₃₂ не войдет в общую сумму.

Самое интересное – это ограничения. Например, грузовик i не может поехать к двум клиентам в одно и то же время. Это можно записать в виде ограничения:

 

x   _i1t + x   _i2t ≤, i    =1,2,3,4; t    =1,2.

 

Тогда для любого i и t только одно (или ни одно) из значений х _i1t или х _i2t может равняться единице.

Еще одно универсальное ограничение: к клиенту j нужно послать только один грузовик, то есть

 

 

Ограничения могут учитывать особенности каждого грузовика, клиента и другие факторы. Например, мы не хотим, чтобы грузовик 3 работал утром (скажем, у этого грузовика запланирован техосмотр). Тогда мы просто включим ограничение:

 

x   ₃₁₁ + x   ₃₂₁ = 0.

 

Теперь допустим, что это условие желательное, но необязательное. Тогда к целевой функции можно добавить дополнительное слагаемое, которое будет означать штраф за невыполнение условия:

 

c   _штраф (x   ₃₁₁ + x   ₃₂₁).

 

Заметьте, что это слагаемое действительно добавится, только если грузовик 3 работал в утреннюю смену. Естественно, оптимальное решение будет зависеть от коэффициента c _штраф. Если он больше любого c_ij в целевой функции, то оптимальный вариант – не задействовать грузовик 3 с утра. А если коэффициент с _штраф маленький, то, возможно, грузовик 3 все равно задействуют, если это обеспечит более низкую цену доставки.

В виде линейных ограничений можно записать самые разные условия. Например, мы хотим, чтобы грузовик 3 либо работал, либо не работал обе половины дня. Тогда мы вводим ограничение

 

x   ₃₁₁ + x   ₃₂₁ = x   ₃₁₂ + x   ₃₂₂. (П.2)

 

Это условие можно несколько усложнить. Например, если грузовик 3 в первой половине дня поехал к клиенту 1, то мы хотим, чтобы он работал и во второй половине дня. Как это записать в виде линейного неравенства? Часто используется такой прием. Вводим достаточно большое значение М и записываем:

 

(x   ₃₁₁ + x   ₃₂₁) − (x   ₃₁₂ + x   ₃₂₂) ≤ M (1 − x   ₃₁₁).

 

Если x ₃₁₁=1, то значение справа при любом М равно нулю. Тогда неравенство выполняется (и на самом деле является равенством), только если x ₃₁₂ + x ₃₂₂=1 (вспомните, что x ₃₁₁ + x ₃₂₁=1). Но если x ₃₁₁=0, то М можно выбрать достаточно большим, чтобы ограничение не играло никакой роли. В данном случае, кстати, достаточно, чтобы М =1. Для увеличения скорости решения М стараются выбирать «экономно» – не больше, чем нужно.

Есть еще множество интересных приемов записи обязательных и желательных условий в виде линейных выражений, но их более подробное описание выходит за рамки нашей книги.

 

Идея метода ветвей и границ

 

Допустим, нам нужно послать землекопов на объекты и мы хотим минимизировать стоимость работ. Для начала мы берем совершенно произвольное расписание и получаем стоимость работ, скажем 50 000 рублей. Это наш максимум, и мы постараемся его уменьшить.

Теперь запускаем симплекс‑метод и получаем дробное решение. Например, на объект А нужно отправить 2 и 2/3 землекопа. Допустим, общая стоимость работ при этом составит 40 000 рублей. Это пока не дает нам плана работ, потому что решение не в целых числах. Зато мы знаем, что это решение оптимальное, то есть при любом другом (в том числе целочисленном) решении стоимость получится никак не меньше 40 000 рублей. Значит, наша стоимость в результате будет между 40 000 и 50 000 рублей.

Дальше начинаем «разветвлять» решение. У нас есть два варианта: A ≤ 2 и A  ≥ 3. Для каждого из них мы снова решаем задачу линейного программирования. Допустим, стоимость получилась 43 000 рублей при A ≥ 3 и 51 000 при A ≤ 2. Отсекаем вариант A ≤ 2, поскольку у нас уже есть более выгодное решение. В результате делаем вывод, что A ≥ 3, а минимальная стоимость теперь 43 000 рублей. Если при этом все переменные получились целочисленные, то мы нашли решение. А если у нас еще остались дробные переменные, то каждую из них разветвляем снова. И так до тех пор, пока не найдем решения в целых числах.

Назад к Главе 2

 

 

Приложения к главе 3