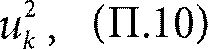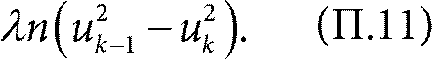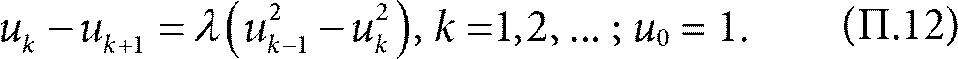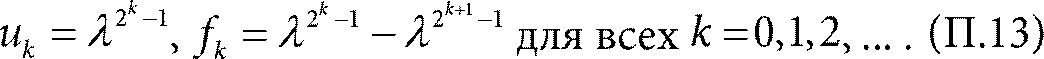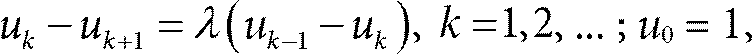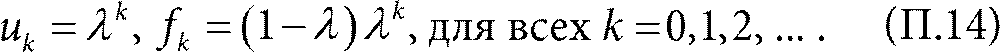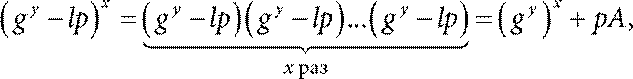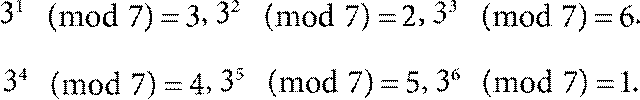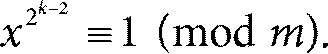Анализ метода выбора из двух

 

Допустим, у нас n серверов. Заявки (или задания) поступают с интенсивностью λ_n в единицу времени, и каждый сервер в среднем обрабатывает одно задание в единицу времени, то есть загрузка системы равна λ < 1 (если λ ≥1, то система перегружена, очередь будет расти до бесконечности). Рассмотрим случай, когда n очень велико и стремится к бесконечности.

Обозначим через f_k долю серверов, у которых ровно k заявок (заявка, которая находится на обслуживании в данный момент, тоже учитывается). Обозначим через u_k долю серверов, у которых заявок k или больше. Значения u_k можно легко получить через f_k и наоборот:

 

 

Понятно, что u ₀ = 1.

Представим, что система находится в равновесии. Тогда у нас в среднем

 

 

серверов, на которых ровно k заданий. Все эти серверы обрабатывают задания со скоростью одно задание в единицу времени. Другими словами, количество серверов с k заявками или больше уменьшается на n (u_k − u_k+1) в единицу времени.

Теперь давайте посмотрим, на сколько количество серверов с k заявками или больше увеличивается в единицу времени. Чтобы увеличить число таких серверов, заявки должны поступать на серверы, у которых в данный момент k − 1 заявка. При методе выбора из двух вероятность того, что новое задание попадет на сервер с k или больше заявками, равна

 

 

потому что в этом случае оба случайно и независимо выбранных сервера должны иметь k или больше заявок, и для каждого из двух серверов эта вероятность и_k [26]. Значит, вероятность того, что новая заявка поступит на сервер, у которого ровно k − 1 заявка, равна

 

 

Поскольку заявок в единицу времени поступает λ п, то получается, что число серверов с k или больше заявками в единицу времени в среднем увеличивается на

 

 

Так как система находится в равновесии, число серверов с k или больше заявками должно оставаться неизменным, то есть (П.9) равняется (П.11). Отсюда получаем уравнение баланса:

 

 

Результат, приведенный в работе {34}, говорит, что при определенных общепринятых предположениях о законе поступления заданий и времени их выполнения, в пределе для бесконечного количества серверов, уравнение (П.12) действительно описывает равновесное состояние системы. Это достаточно сложный технический результат. Нетрудно проверить или даже догадаться, что решение уравнения (П.12) задается формулами:

 

 

Это так называемый двойной экспоненциальный закон. Двойка в формуле, та самая двойка – вторая степень – из выражения (П.10). Точно так же мы могли бы выбирать не из двух, а из r серверов и получили бы

 

 

Интересно заметить, что при тех же предположениях, но случайном выборе одного сервера, изменятся выражения (П.10) и, соответственно, (П.11). Действительно, на этот раз заявка выбирает только один сервер и вероятность попасть на сервер с k или больше заявками равна просто и_k. Тогда вместо (П.12) получаем классическое уравнение баланса:

 

 

решение которого задается известной формулой Эрланга:

 

 

Очевидно, что и_k в формуле (П.13) убывает гораздо быстрее.

Именно эти формулы мы использовали в табл. 5.1. В нашем случае λ = 0,9, и в таблице мы привели значения f_k. В первой колонке – значения k, во второй – значения f_k, подсчитанные по формуле (П.14), в третьей – значения f_k, подсчитанные по формуле (П.13).

Назад к Главе 5

 

 

Приложения к главе 6

 

Схема Диффи – Хеллмана

 

Для начала введем обозначения. Пусть р – заданное простое число, g – заданное натуральное число, g < p. На самом деле g это так называемый первообразный корень числа р. Об этом мы расскажем ниже, в приложении 2 и приложении 3 к главе 6. Цель данного раздела – доказать, что в схеме Диффи – Хеллмана Алиса и Боб действительно получают один и тот же ключ.

Для любых натуральных чисел n и р мы воспользуемся стандартным обозначением для остатка от деления n на р:

 

n   (mod p   ) = [остаток от деления n    на p   ].

 

(Читается «n по модулю p».)

Итак, Алиса задумала число х, а Боб число у. Схема Диффи – Хеллмана состоит из двух шагов.

 

Шаг 1. Алиса передает Бобу

 

a    = (g^x   ) (mod p   ).

 

Боб передает Алисе

 

b    = (g^y   ) (mod p   ).

 

Шаг 2. Алиса вычисляет ключ

 

K_A    = (b^x   ) (mod p   ).

 

Боб вычисляет ключ

 

K_B    = (a^y   ) (mod p   ).

 

Утверждение. Боб и Алиса получили один и тот же ключ K = K_A = K_B.

Доказательство. Нам нужно доказать, что K_A = K_B. Поскольку а и b – это остатки от деления на р, то существуют такие целые числа k и l, при которых

 

a    = g^x    − kp, b    = g^y    − lp  .

 

Подставив эти выражения в формулы для ключей, получаем:

 

K_A    = (g^y    − lp   ) ^x    (mod p   ),

K_B    = (g^x    − kp)^y    (mod p   ).

 

Заметим, что в выражении для K_A можно расписать (g^y − lp) ^x следующим образом:

 

 

где А – это целое число, то есть рА делится на р. Таким образом получаем

 

K_A    = ((g^y    − lp   ) ^x   ) (mod p   ) = ((g^y   ) ^x    + pA   ) (mod p   ) = (g^y   ) ^x    (mod p   ).

 

Совершенно аналогично для какого‑то целого числа B получаем

 

K_B    = ((g^x    − kp   ) ^y   ) (mod p   ) = ((g^x   ) ^y    + pB   ) (mod p   ) = (g^x   ) ^y    (mod p   ).

 

Результат теперь очевиден, поскольку

 

(g^y   ) ^x    = g^yx    = g^xy    = (g^x   ) ^y  .

 

Дискретное логарифмирование

 

Вспомним, что логарифм числа у по основанию g – это такое число х, для которого выполняется

 

g^x    = y  .

 

Легко заметить, что очень похожая операция лежит в основе схемы Диффи – Хеллмана.

После возведения в степень мы берем остаток от деления на р. Как мы уже упоминали выше, в математике такая операция обозначается g^x (mod p) (читается «g в степени х по модулю р»). При этом, естественно, g и х натуральные числа и у g нет общих делителей с р.

Одна нетривиальная теорема из теории чисел (см., например, {35}) утверждает, что для каждого простого р существует такое число g, что все числа

 

 

разные, то есть служат перестановкой множества 1, 2, …, p − 1 (среди них нет нуля, поскольку g < p и, значит, g^х не делится на р). Например,

 

 

Из этого следует возможность корректного определения дискретного логарифма, который еще называется индексом. А именно: «логарифм» произвольного числа y ∈ {1, 2, …, p − 1} по основанию g – это тот самый, уникальный, x ∈ {1, 2, …, p − 1}, при котором выполняется g^x (mod p) = y. Поскольку для всех x < p остатки разные, то х определяется однозначно. Операция нахождения такого х называется операцией дискретного логарифмирования. Она очень сложная, и никто не знает, можно ли придумать способ ее быстрой реализации.

Как определить такое число g, чтобы все остатки в выражении (П.15) были разные? Число g обладает этим свойством, если оно является первообразным корнем числа р. Мы позволим себе рассказать об этом понятии немножко подробнее.

 

Первообразные корни

 

Есть такая теорема Эйлера: если х и m взаимно просты, то g ^{φ (m)}  ≡ 1. Здесь a ≡ b, если a − b делится на m. Другими словами, у а и b одинаковый остаток от деления на m. А φ (m) это функция Эйлера, равная количеству чисел, не превосходящих m и взаимно простых с ним. Например, если m = p, где р простое, то φ (p) = p − 1 и теорема Эйлера превращается в малую теорему Ферма.

Условие теоремы Эйлера достаточное, но не необходимое. Вполне может случиться и так, что x^a ≡ 1 (mod m), хотя a < φ (m). Самый простой пример такой ситуации – это, конечно, x = 1. Действительно, x^a ≡ 1 (mod m) для любых натуральных a и m. Но есть и менее тривиальные примеры. Скажем, p = 5, а 4² = 16 ≡ 1(mod 5), хотя 2 < p − 1 = 4.

Формально число g называется первообразным корнем по модулю m, если

 

 

g ^{φ (m)}  ≡ 1 (mod m), но g^a ≢ 1 (mod m) при всех a < φ (m) и a ≠ 0.

 

Пример (отсутствие первообразных корней у m    = 2 ^k   ). Возьмем m = 2 ^k при k ≥ 3. В этом случае можно показать, что для любого натурального х выполняется

 

 

При этом φ (m) = 2 ^{k −1}, потому что числа, взаимно простые со степенью двойки, – это все нечетные числа, а их ровно 2 ^{k −1}. Значит, для любого х нашлось число

 

a = 2 ^{k −2} < 2 ^{k −1} = φ (m),

 

для которого выполняется x^a ≡ 1 (mod m). Получается, что у m = 2 ^k при k ≥ 3 первообразных корней нет.

Теперь мы можем объяснить, почему в качестве m удобно брать простое число р. Для простого р всегда существуют первообразные корни. На самом деле мы уже говорили о них выше, в приложении 2 к главе 6, только не называли этим термином. Это те самые числа g, которые дают разные остатки от деления на p в (П.15). Например, при p = 3 это g = 2, при p = 5 это g = 2, а при p = 7 это g = 3. В нашем примере в тексте главы число g = 2 – это один из первообразных корней числа p = 19.

Итак, если g – первообразный корень p, то все остатки в (П.15) разные и каждому остатку соответствует единственная степень х (дискретный логарифм, он же индекс), при которой такой остаток получается. Ничего подобного мы не можем сделать, если будем брать остаток от деления на число m, для которого первообразного корня нет. Именно поэтому работают с простыми числами.

Заметим, что первообразные корни есть еще для m = 4, m = p^k и m = 2 p^k. Но все равно с простыми числами работать проще.

Назад к Главе 6

 

 

Приложение к главе 7