Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Имитационное моделирование 3 курс (56 часов, в том числеСтр 1 из 14Следующая ⇒
ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ 3 курс (56 часов, в том числе Лекции – 28 часов, Лабы – 28 часов) Литература: 1. Советов Б.Я., Яковлев С.А. Моделирование систем. Учебник для вузов (М. ВШ, 2001 - 343с) 2. Дьяконов В.П. MatLab 6.5 / Simulink 5/6 Основы применения (М, СОЛОН-Пресс, 2005 - 800с) 3. Черных И.В. Simulink. Инструмент моделирования динамических систем.
ЧАСТЬ 1. МОДЕЛИРОВАНИЕ СИСТЕМ Лекция №1. Глава 1. Понятие моделирования. Модель – это объект-заместитель оригинала, обеспечивающий некоторые его свойства. Таким образом, моделирование - это замещение одного объекта другим с целью получения информации о важнейших свойствах оригинала. Адекватность модели реальному объекту зависит от цели моделирования и принятых критериев. Адекватность проверяется экспериментально. Практика является критерием истинности объекта. Процесс моделирования предполагает наличие объекта, исследователя, модели, созданной исследователем. Исследователь ставит эксперименты с моделями. Моделирование – это основной метод исследований во всех областях знаний и научно обоснованный метод оценок характеристик сложных систем, используемый для принятия решений в различных сферах деятельности.
Этапы моделирования систем Постановка цели моделирования. Любую модель строят в зависимости от цели, которую ставит перед ней исследователь, поэтому одна из основных проблем при моделировании — это проблема целевого назначения. Подобие процесса, протекающего в модели М, реальному процессу является не целью, а условием правильного функционирования модели, и поэтому в качестве цели должна быть поставлена задача изучения какой-либо стороны функционирования объекта. Для упрощения модели М цели делят на подцели и создают более эффективные виды моделей в зависимости от полученных подцелей моделирования. Построение модели М. Построение модели оказывается возможным, если имеется информация или выдвинуты гипотезы относительно структуры, алгоритмов и параметров исследуемого объекта. На основании их изучения осуществляется идентификация объекта. В настоящее время широко применяют различные способы оценки параметров: по методу наименьших квадратов, по методу максимального правдоподобия и т.п..
3. Реализация модели. Основные задачи реализации — минимизация времени получения конечных результатов и обеспечение их достоверности. Для правильно построенной модели М характерным является то, что она выявляет лишь те закономерности, которые нужны исследователю, и не рассматривает свойства системы S, не существенные для данного исследования. Следует отметить, что оригинал и модель должны быть одновременно сходны по одним признакам и различны по другим, что позволяет выделить наиболее важные изучаемые свойства. В этом смысле модель выступает как некоторый «заместитель» оригинала, обеспечивающий фиксацию и изучение лишь некоторых свойств реального объекта.
Лекция № 2 Классификация видов моделирования систем.
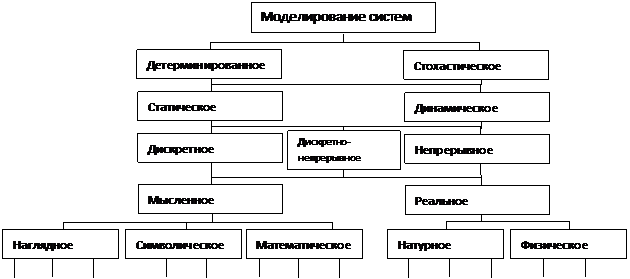
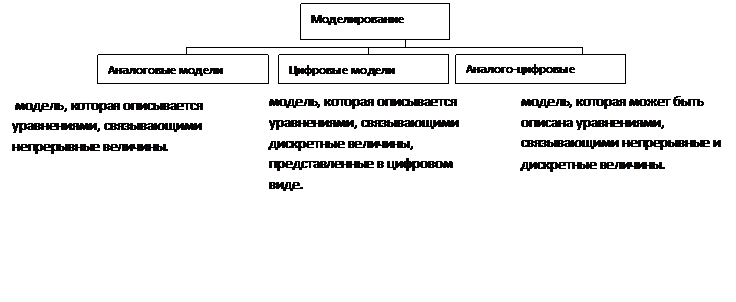
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании абсолютное подобие не имеет места и стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта. Классификационные признаки. 1. В качестве одного из первых признаков классификации видов моделирования можно выбрать степень полноты модели и разделить модели в соответствии с этим признаком на 1.1. полные, 1.2. неполные и 1.3.приближенные. В основе полного моделирования лежит полное подобие, которое проявляется как во времени, так и в пространстве. Для неполного моделирования характерно неполное подобие модели изучаемому объекту. В основе приближенного моделирования лежит приближенное подобие, при котором некоторые стороны функционирования реального объекта не моделируются совсем. Классификация видов моделирования в зависимости от характера изучаемых процессов и в зависимости от формы представления объекта приведена на рис.
. .
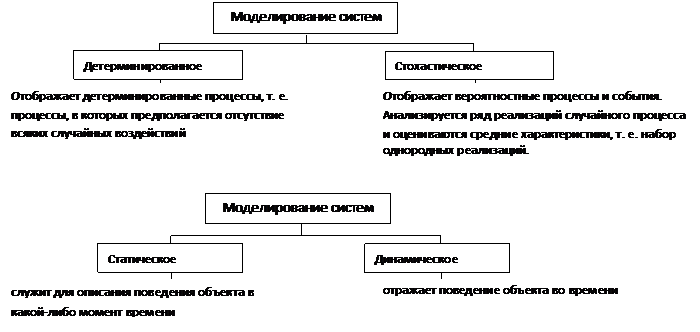
2. В зависимости от характера изучаемых процессов в системе все виды моделирования могут быть разделены на
– детерминированные и стохастические, – статические и динамические, – дискретные, непрерывные и дискретно-непрерывные.
3. В зависимости от формы представления объекта можно выделить мысленное и реальное моделирование.
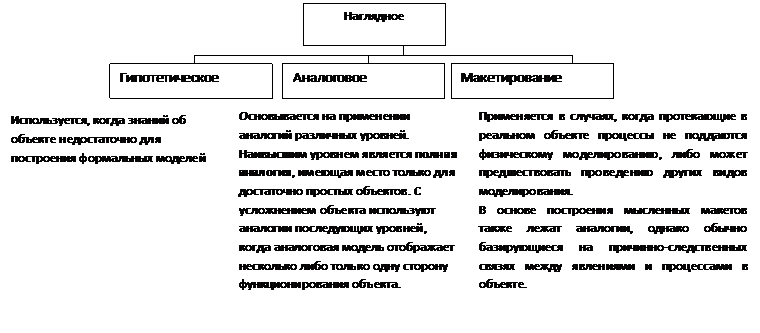
3.1. Мысленное моделирование может быть реализовано в виде наглядного, символического и математического.
3.1.1.
3.1.2.
3.1.3
Когда результаты, полученные при воспроизведении на имитационной модели процесса функционирования системы S, являются реализациями случайных величин и функций, тогда для нахождения характеристик процесса требуется его многократное воспроизведение с последующей статистической обработкой информации и целесообразно в качестве метода машинной реализации имитационной модели использовать метод статистического моделирования. Первоначально был разработан метод статистических испытаний, представляющий собой численный метод, который применялся для моделирования случайных величин и функций, вероятностные характеристики которых совпадали с решениями аналитических задач (такая процедура получила название метода Монте-Карло). Затем этот прием стали применять и для машинной имитации с целью исследования характеристик процессов функционирования систем, подверженных случайным воздействиям, т. е. появился метод статистического моделирования. Таким образом, методом статистического моделирования будем в дальнейшем называть метод машинной реализации имитационной модели, а методом статистических испытаний (Монте-Карло) — численный метод решения аналитической задачи. Метод имитационного моделирования позволяет решать задачи анализа больших систем S, включая задачи оценки: вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы.
3.2. Рассмотрим разновидности реального моделирования.
4. С точки зрения математического описания объекта и в зависимости от его характера модели можно разделить на модели аналоговые (непрерывные), цифровые (дискретные) и аналого-цифровые (комбинированные).
Лекция № 3. Формальная модель объекта Каждая конкретная система S характеризуется набором свойств, т.е. величинами, отражающими поведение моделируемого объекта (реальной системы), при этом учитываются условия её функционирования во взаимодействии с внешней средой (системой) Е. При построении модели системы S необходимо решить вопрос о её полноте. Полнота моделирования регулируется, в основном, выбором границ "Система S — среда Е". Также должна быть решена задача упрощения модели, которая помогает выделить основные свойства системы, отбросив второстепенные в плане цели моделирования. Модель объекта моделирования, т.е. системы S можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:
- совокупность Х - входных воздействий на S хiÎХ, i=1…nx; - совокупность воздействий внешней среды vlÎV, l=1…nv; - совокупность внутренних (собственных) параметров системы hkÎH, k=1…nh; - совокупность выходных характеристик системы yjÎY, j=1…ny.
В перечисленных множествах можно выделить управляемые и неуправляемые величины. В общем случае X, V, H, Y не пересекаемые множества, содержат как детерминированные, так и стохастические составляющие. Входные воздействия, воздействия внешней среды и внутренние параметры системы являются независимыми (экзогенными) переменными, Выходные характеристики - зависимые переменные (эндогенные)
Процесс функционирования S описывается оператором FS:
Алгоритм функционирования AS — метод получения выходных характеристик
Очевидно один и тот же FS может быть реализован различными способами, т.е. с помощью множества различных AS. Соотношение (1) является математическим описанием поведения объекта S моделирования во времени t, т.е. отражает его динамические свойства. (1) - это динамическая модель системы S.
Состояния системы S характеризуются векторами zk. Совокупность всех возможных значений состояний { Состояние системы S в интервале времени t 0 < t £ Tl полностью определяется начальными условиями
иначе:
Время в мод. S может рассматриваться на интервале моделирования (t0, T) как непрерывное, так и дискретное, т.е. квантованное на отрезке длиной Dt. Таким образом, под моделью объекта понимаем конечное множество переменных { Моделирование называется детерминированным, если операторы F, Ф детерминированные, т.е. для конкретного входа выход детерминированный. Детерминированное моделирование - частный случай стохастического моделирования. В практике моделирование объектов в области системного анализа на первичных этапах исследования рациональнее использовать типовые математические схемы: диф. уравнения, конечные и вероятностные автоматы, СМО и т.д. Типовые схемы: 1) Дифференциальные и разностные уравнения 2) Конечные вероятностные автоматы 3) Стохастические дифф. ур. 4) Системы МО 5) Сети Петри и т.п. 6) Типовые агрегированные схемы Aгрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивая взаимодействие частей. Подходы в типовых схемах: 1. Непрерывный детерминированный 2. Дискретный детерминированный 3. Дискретный стохастический 4. Непрерывный стохастический 5. Обобщенный 6. Универсальный Двухточечная краевая задача
Для ее решения в линейном случае используется метод прогонки.
Используем метод прогонки для решения системы ДУ:
Собираем коэффициенты при
Собираем свободные члены:
В точке
Поскольку
Это задача Коши, которую надо решать в обратном времени.
Решение этого однородного линейного ДУ с граничным условием, равным точке покоя есть точка покоя:
С учетом этого
Тогда уравнение замкнутой системы (управляемой):
Уравнение для
Если заменить
Тогда получим субоптимальное управление:
Для линеаризованной системы управления
Поскольку
КОЛЛОКВИУМ по 3 лекциям
Лекция №4. 2.3. Дискретно-детерминированные модели (F-схемы). Конечные автоматы Особенности дискретно-детерминированного подхода на этапе формализации процесса функционирования систем рассмотрим на примере использования в качестве математического аппарата теории автоматов. Теория автоматов — это раздел теоретической кибернетики, в котором изучаются математические модели — автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции целесообразной степени общности. Основные соотношения. Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами. Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами: конечным множеством X входных сигналов (входным алфавитом); конечным множеством Y выходных сигналов (выходным алфавитом); конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием z0, z0?Z; функцией переходов функцией выходов Автомат, задаваемый F-схемой
Обозначим состояние, а также ВХОДНОЙ и выходной сигналы, соответствующие t-му такту при t=0, 1, 2,..., через z(t), x(t), y(t). При этом, по условию, z(0)=zo, a z(t)?Z, x(t)? X, y(t)?Y. Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент t=0, 1, 2,... дискретного времени F-автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=zo. В момент t, будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал x(t)?X и выдать на выходном канале сигнал давать в некоторой последовательности буквы входного алфавита х(0), x(1), x(2),..., т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита у(0), y(1), у(2),..., образуя выходное слово. Таким образом, работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t + 1) и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для F-автомата первого рода, называемого также автоматом Мили,
для F -автомата второго рода
Автомат второго рода, для которого
т. е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.
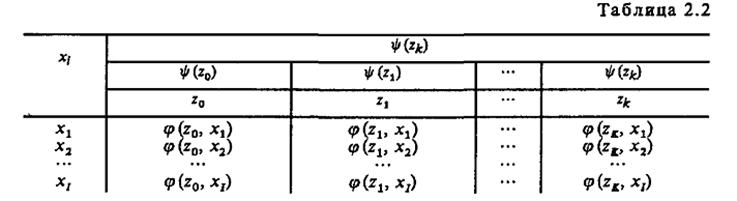
По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определенный выходной сигнал y(t), т. е. реализует логическую функцию вида Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов х и у, состоят из двух букв. По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F-автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F-автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом. Способы задания: табличный, графический, матричный. 1. Табличное задание автомата - задание таблиц переходов и выходов. Строки такой таблицы - входные сигналы, столбцы - выходы (состояния). Рассмотрим для примера табличное задание автомата Мили.
Таблица переходов для автомата Мура:
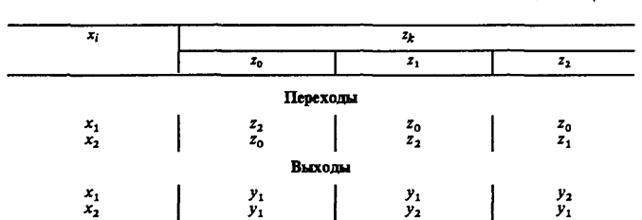
Пример табличного задания F-автомата Мили с тремя состояниями:
Автомат Мура с 5 состояниями:
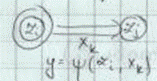
2. При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал хк вызывает переход из состояния zi в состояние zj, то на графе автомата дуга, соединяющая вершину zi с вершиной zj, обозначается хк. Для того, чтобы задать функцию выходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили эта разметка производится так: если входной сигнал хк действует на состояние zi то, согласно сказанному, получается дуга, исходящая из zi и помеченная хк; эту дугу дополнительно отмечают выходным сигналом Граф автомата Мили:
Граф автомата Мура:
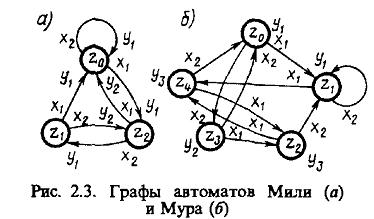
Графы для наших двух примеров будут выглядеть так:
3. При решении задач моделирования систем часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица
Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к графическому способу задания F-автомата это означает, что в графе автомата из любой вершины не могут выходить два ребра и более, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза. Рассмотрим вид таблицы переходов и графа асинхронного конечного автомата. Для F-автомата состояние zk называется устойчивым, если для любого входа Необходимо отметить, что вообще на практике автоматы всегда являются асинхронными, а устойчивость их состояний обеспечивается тем или иным способом, например введением сигналов синхронизации.
2.4. Дискретно-стохастические модели (P-схемы). Вероятностные автоматы
Основные соотношения. В общем виде вероятностный автомат (англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Рассмотрим множество G, элементами которого являются всевозможные пары (xi zs), где xi и zs — элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции
Лекция №5. Лекция №6. Лекция №7. Лекция №8. Примеры статистического моделирования Метод серединных квадратов. Одной из исторически первых процедур получения псевдослучайных чисел была процедура, получившая название метода серединных квадратов. Пусть имеется 2n-разрядное число, меньшее 1: Недостаток этого метода — наличие корреляции между числами последовательности, а в ряде случаев случайность вообще может отсутствовать. Например, если х0=0,4500, то 3. Конгруэнтные процедуры генерации. Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации псевдослучайных последовательностей, представляющие собой арифметические операции, в основе которых лежит фундаментальное понятие конгруэнтности. Два целых числа Конгруэнтные процедуры являются чисто детерминированными, так как описываются в виде рекуррентного соотношения, когда функция Ф имеет вид
где Раскроем данное рекуррентное соотношение:
…,
Если заданы начальное значение Х0, множитель Мультипликативный метод. Задает последовательность неотрицательных целых чисел {Xi}, не превосходящих М, по формуле
т. е. это частный случай соотношения (**) при В силу детерминированности метода получаются воспроизводимые последовательности. Требуемый объем машинной памяти при этом минимален, а с вычислительной точки зрения необходим последовательный подсчет произведения двух целых чисел, т. е. выполнение операции, которая быстро реализуется современными ЭВМ. Для машинной реализации наиболее удобна версия запятой. Алгоритм построения последовательности для двоичной машины 1. Выбрать в качестве Х0 произвольное нечетное число. 2. Вычислить коэффициент 3. Найти произведение 4. Взять g младших разрядов в качестве первого члена последовательности Х1 а остальные отбросить. 5. Определить дробь 6. Присвоить X0=X1. 7. Вернуться к п. 3. Пример. Необходимо получить числа последовательности для случая g=4, используя приведенный алгоритм мультипликативного метода. Для этого выполняем следующие действия: 1. Выбираем X010=7 (в десятичной системе счисления) или X0=0111 (в двоичной системе счисления). 2. Найдем t=1, тогда 3. Рассчитываем произведение а) б) в)
| Поделиться:
| | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||







 .
.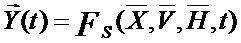 (1)
(1)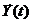 - выходная траектория. FS - закон функционирования S. FS может быть функция, функционал, логические условия, алгоритм, таблица или словесное описание правил.
- выходная траектория. FS - закон функционирования S. FS может быть функция, функционал, логические условия, алгоритм, таблица или словесное описание правил.
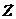 } называется пространством состояний объекта моделирования Z, причём zkÎZ.
} называется пространством состояний объекта моделирования Z, причём zkÎZ. , где
, где 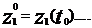 входными воздействиями
входными воздействиями 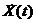 , внутренними параметрами
, внутренними параметрами 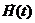 и воздействиями внешней среды
и воздействиями внешней среды 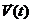 , которые имели место за промежуток времени t * - t 0 c помощью 2-х векторных уравнений:
, которые имели место за промежуток времени t * - t 0 c помощью 2-х векторных уравнений: ; (3)
; (3)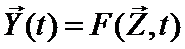 . (4)
. (4) . (5)
. (5) } вместе с математическими связями между ними и характеристиками
} вместе с математическими связями между ними и характеристиками 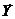 .
.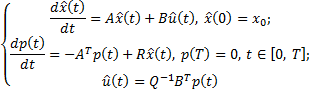
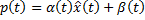
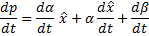

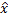 :
:
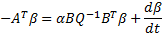
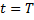 :
:
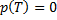 , то
, то 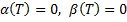
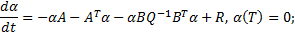
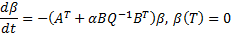
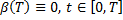
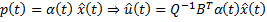
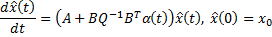
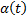 имеет квадратичную правую часть. Это уравнение Риккати (Riccati).
имеет квадратичную правую часть. Это уравнение Риккати (Riccati).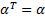 – симметричная матрица
– симметричная матрица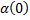 , то система остается управляемой, но управление становится немного хуже.
, то система остается управляемой, но управление становится немного хуже.
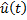 (или
(или 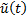 ) является оптимальным (субоптимальным).
) является оптимальным (субоптимальным). , то
, то 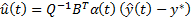 (или
(или 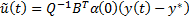 ), то для нелинейной системы получаем
), то для нелинейной системы получаем (или
(или 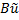 ),
), 
 ;
;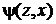 .
.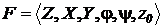 — функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
— функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. , переходя в состояние
, переходя в состояние  , z(t)?Z, y(t)? Y. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, по
, z(t)?Z, y(t)? Y. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, по
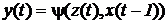 ,
,  ,
, 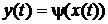 ,
, 

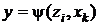 . Для автомата Мура аналогичная разметка графа такова: если входной сигнал хк, действуя на некоторое состояние автомата, вызывает переход в состояние zj, то дугу, направленную в zj и помеченную хк, дополнительно отмечают выходным сигналом
. Для автомата Мура аналогичная разметка графа такова: если входной сигнал хк, действуя на некоторое состояние автомата, вызывает переход в состояние zj, то дугу, направленную в zj и помеченную хк, дополнительно отмечают выходным сигналом 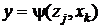 .
.
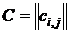 , строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Элемент
, строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Элемент 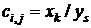 , стоящий на пересечении i-й строки и j-ro столбца, в случае автомата Мили соответствует входному сигналу хк, вызывающему переход из состояния zi в состояние Zj, и выходному сигналу ys, выдаваемому при этом переходе. Для автомата Мили, рассмотренного выше, матрица соединений имеет вид
, стоящий на пересечении i-й строки и j-ro столбца, в случае автомата Мили соответствует входному сигналу хк, вызывающему переход из состояния zi в состояние Zj, и выходному сигналу ys, выдаваемому при этом переходе. Для автомата Мили, рассмотренного выше, матрица соединений имеет вид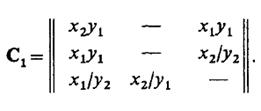

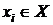 , для которого
, для которого 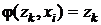 , имеет место
, имеет место 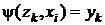 . Таким образом, F-автомат называется асинхронным, если каждое его состояние
. Таким образом, F-автомат называется асинхронным, если каждое его состояние 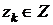 устойчиво.
устойчиво.
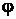 и
и 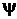 , то с их помощью осуществляются отображения G->Z и G->Y, то говорят, что F= <Z, X, Y,
, то с их помощью осуществляются отображения G->Z и G->Y, то говорят, что F= <Z, X, Y, 
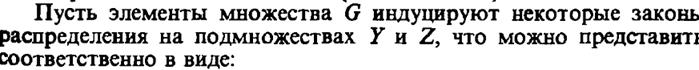


 . Возведем его в квадрат:
. Возведем его в квадрат:  , а затем отберем средние 2n разрядов
, а затем отберем средние 2n разрядов  , которые и будут являться очередным числом псевдослучайной последовательности. Например, если начальное число
, которые и будут являться очередным числом псевдослучайной последовательности. Например, если начальное число 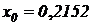 ,
, 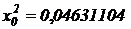 , т. е.
, т. е. 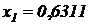 , затем
, затем 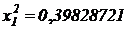 , т.е.
, т.е.  , и т. д.
, и т. д. ,
, 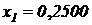 ,
, 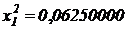 ,
,  ,
, 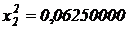 ,
, 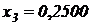 и т. д. Кроме того, при некоторых i* вообще может наблюдаться вырождение последовательности, т. е.
и т. д. Кроме того, при некоторых i* вообще может наблюдаться вырождение последовательности, т. е.  ,
,  и
и  конгруэнтны (сравнимы) по модулю m, где m — целое число, тогда и только тогда, когда существует такое целое число k, что
конгруэнтны (сравнимы) по модулю m, где m — целое число, тогда и только тогда, когда существует такое целое число k, что  , т. е. если разность
, т. е. если разность 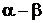 делится на m и если числа
делится на m и если числа 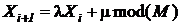 , (**)
, (**) ,
,  ,
,  ,
, 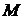 – — неотрицательные целые числа.
– — неотрицательные целые числа. ,
, ,
,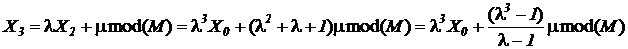 ,
,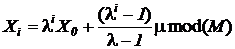 .
. . Таким образом, для любого i>=1 справедливо неравенство Xi<M. По целым числам последовательности {Xi} можно построить последовательность
. Таким образом, для любого i>=1 справедливо неравенство Xi<M. По целым числам последовательности {Xi} можно построить последовательность 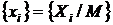 рациональных чисел из единичного интервала (0, 1). Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо смешанным методом.
рациональных чисел из единичного интервала (0, 1). Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо смешанным методом.
 .
. , где р — число цифр в системе счисления, принятой в ЭВМ (р=2 для двоичной и р= 10 для десятичной машины); g — число битов в машинном слове. Тогда вычисление остатка от деления на М сводится к выделению g младших разрядов делимого, а преобразование целого числа Х(в рациональную дробь из интервала
, где р — число цифр в системе счисления, принятой в ЭВМ (р=2 для двоичной и р= 10 для десятичной машины); g — число битов в машинном слове. Тогда вычисление остатка от деления на М сводится к выделению g младших разрядов делимого, а преобразование целого числа Х(в рациональную дробь из интервала  осуществляется подстановкой слева от X, двоичной или десятичной
осуществляется подстановкой слева от X, двоичной или десятичной в сводится к выполнению таких операций:
в сводится к выполнению таких операций: , где t — любое целое положительное число.
, где t — любое целое положительное число.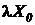 , содержащее не более 2g значащих разрядов.
, содержащее не более 2g значащих разрядов.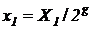 из интервала (0, 1).
из интервала (0, 1). или 5; пусть
или 5; пусть  ,
, 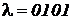 .
.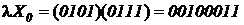 ; X1=0011,
; X1=0011, 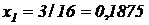 ;
; ; X2=1111,
; X2=1111,