Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывно детерминированные модели (Д - схемы).
Непрерывные детерминированные модели (D-схемы) используют дифференциальные уравнения. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной переменной или нескольких переменных, причём в уравнение входят не только их функции но их производные различных порядков. Если неизвестные - функции многих переменных, то уравнения называются — уравнения в частных производных. Если неизвестные функции одной независимой переменной, то имеют место обыкновенные дифференциальные уравнения. Математическое соотношение для детерминированных систем в общем виде:
Диф. уравнения, Д - схемы являются математическим аппаратом теории систем автоматического регулирования, управления. В качестве примера D-схемы рассмотрим модель Лотки – Вольтерры системы «хищник-жертва», которая имеет вид:
где y1 – количество жертв, y2 – количество хищников, t – время, a, b, c, g – коэффициенты, отражающие взаимодействия между видами: a – коэффициент рождаемости жертв, g – коэффициент рождаемости хищников, c – коэффициент убыли хищников, b – коэффициент гибели жертв при встрече с хищником. Точка покоя (нетривиальная):
Управляемая система Лотки-Вольтерра имеет вид:
Линеаризуем рассматриваемую систему:
Сделаем замену переменных:
Построим функционал Лагранжа
Подставим в функционал x, u и J:
Возьмем производную и приравняем ее нулю:
Возьмем по частям интеграл:
Тогда
Двухточечная краевая задача
Для ее решения в линейном случае используется метод прогонки.
Используем метод прогонки для решения системы ДУ:
Собираем коэффициенты при
Собираем свободные члены:
В точке
Поскольку
Это задача Коши, которую надо решать в обратном времени.
Решение этого однородного линейного ДУ с граничным условием, равным точке покоя есть точка покоя:
С учетом этого
Тогда уравнение замкнутой системы (управляемой):
Уравнение для
Если заменить
Тогда получим субоптимальное управление:
Для линеаризованной системы управления
Поскольку
КОЛЛОКВИУМ по 3 лекциям
Лекция №4. 2.3. Дискретно-детерминированные модели (F-схемы). Конечные автоматы Особенности дискретно-детерминированного подхода на этапе формализации процесса функционирования систем рассмотрим на примере использования в качестве математического аппарата теории автоматов. Теория автоматов — это раздел теоретической кибернетики, в котором изучаются математические модели — автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции целесообразной степени общности. Основные соотношения. Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами. Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами: конечным множеством X входных сигналов (входным алфавитом); конечным множеством Y выходных сигналов (выходным алфавитом);
конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием z0, z0?Z; функцией переходов функцией выходов Автомат, задаваемый F-схемой
Обозначим состояние, а также ВХОДНОЙ и выходной сигналы, соответствующие t-му такту при t=0, 1, 2,..., через z(t), x(t), y(t). При этом, по условию, z(0)=zo, a z(t)?Z, x(t)? X, y(t)?Y. Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент t=0, 1, 2,... дискретного времени F-автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=zo. В момент t, будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал x(t)?X и выдать на выходном канале сигнал давать в некоторой последовательности буквы входного алфавита х(0), x(1), x(2),..., т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита у(0), y(1), у(2),..., образуя выходное слово. Таким образом, работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t + 1) и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для F-автомата первого рода, называемого также автоматом Мили,
для F -автомата второго рода
Автомат второго рода, для которого
т. е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.
По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определенный выходной сигнал y(t), т. е. реализует логическую функцию вида Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов х и у, состоят из двух букв. По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F-автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F-автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом.
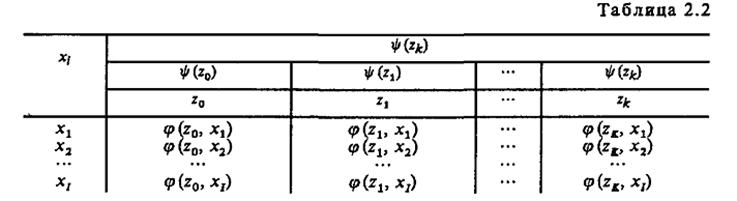
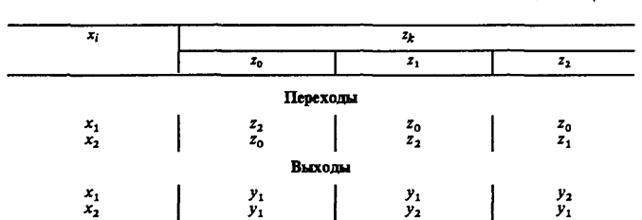
Способы задания: табличный, графический, матричный. 1. Табличное задание автомата - задание таблиц переходов и выходов. Строки такой таблицы - входные сигналы, столбцы - выходы (состояния). Рассмотрим для примера табличное задание автомата Мили.
Таблица переходов для автомата Мура:
Пример табличного задания F-автомата Мили с тремя состояниями:
Автомат Мура с 5 состояниями:
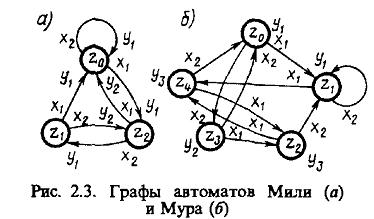
2. При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал хк вызывает переход из состояния zi в состояние zj, то на графе автомата дуга, соединяющая вершину zi с вершиной zj, обозначается хк. Для того, чтобы задать функцию выходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили эта разметка производится так: если входной сигнал хк действует на состояние zi то, согласно сказанному, получается дуга, исходящая из zi и помеченная хк; эту дугу дополнительно отмечают выходным сигналом Граф автомата Мили:
Граф автомата Мура:
Графы для наших двух примеров будут выглядеть так:
3. При решении задач моделирования систем часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица
Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к графическому способу задания F-автомата это означает, что в графе автомата из любой вершины не могут выходить два ребра и более, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза. Рассмотрим вид таблицы переходов и графа асинхронного конечного автомата. Для F-автомата состояние zk называется устойчивым, если для любого входа Необходимо отметить, что вообще на практике автоматы всегда являются асинхронными, а устойчивость их состояний обеспечивается тем или иным способом, например введением сигналов синхронизации.
2.4. Дискретно-стохастические модели (P-схемы). Вероятностные автоматы
Основные соотношения. В общем виде вероятностный автомат (англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Рассмотрим множество G, элементами которого являются всевозможные пары (xi zs), где xi и zs — элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции
Лекция №5.
|
||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.51.117 (0.059 с.) |
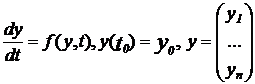 (7).
(7).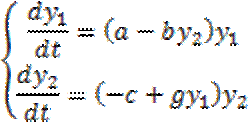 ,
,
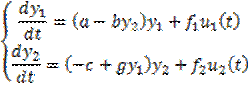
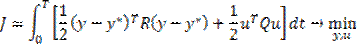



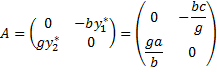
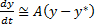 - линеаризованная система
- линеаризованная система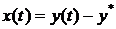
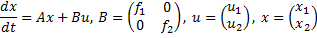

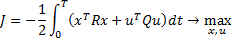
 - положительно определенная матрица (диагональная для простоты),
- положительно определенная матрица (диагональная для простоты), 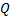 - неотрицательно определенная матрица (диагональная для простоты)
- неотрицательно определенная матрица (диагональная для простоты)
 - оптимальное решение
- оптимальное решение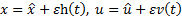 ,
, 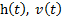 - произвольные функции
- произвольные функции


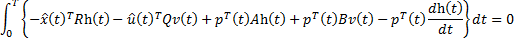
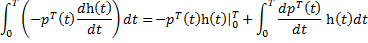
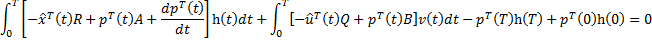

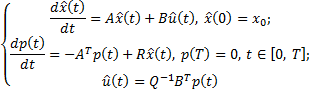
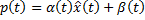
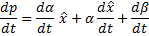

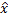 :
:
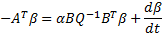
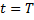 :
:
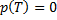 , то
, то 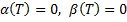
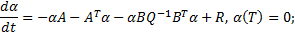
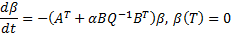
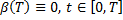
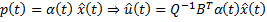
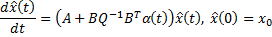
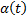 имеет квадратичную правую часть. Это уравнение Риккати (Riccati).
имеет квадратичную правую часть. Это уравнение Риккати (Riccati).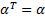 – симметричная матрица
– симметричная матрица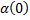 , то система остается управляемой, но управление становится немного хуже.
, то система остается управляемой, но управление становится немного хуже.
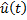 (или
(или 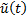 ) является оптимальным (субоптимальным).
) является оптимальным (субоптимальным). , то
, то 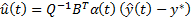 (или
(или 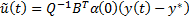 ), то для нелинейной системы получаем
), то для нелинейной системы получаем (или
(или 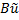 ),
), 
 ;
;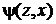 .
.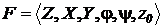 — функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
— функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. , переходя в состояние
, переходя в состояние  , z(t)?Z, y(t)? Y. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, по
, z(t)?Z, y(t)? Y. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, по
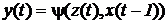 ,
,  ,
, 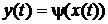 ,
, 

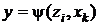 . Для автомата Мура аналогичная разметка графа такова: если входной сигнал хк, действуя на некоторое состояние автомата, вызывает переход в состояние zj, то дугу, направленную в zj и помеченную хк, дополнительно отмечают выходным сигналом
. Для автомата Мура аналогичная разметка графа такова: если входной сигнал хк, действуя на некоторое состояние автомата, вызывает переход в состояние zj, то дугу, направленную в zj и помеченную хк, дополнительно отмечают выходным сигналом 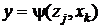 .
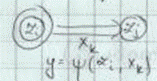
.
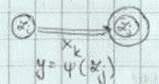
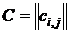 , строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Элемент
, строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Элемент 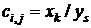 , стоящий на пересечении i-й строки и j-ro столбца, в случае автомата Мили соответствует входному сигналу хк, вызывающему переход из состояния zi в состояние Zj, и выходному сигналу ys, выдаваемому при этом переходе. Для автомата Мили, рассмотренного выше, матрица соединений имеет вид
, стоящий на пересечении i-й строки и j-ro столбца, в случае автомата Мили соответствует входному сигналу хк, вызывающему переход из состояния zi в состояние Zj, и выходному сигналу ys, выдаваемому при этом переходе. Для автомата Мили, рассмотренного выше, матрица соединений имеет вид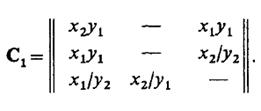

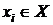 , для которого
, для которого 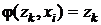 , имеет место
, имеет место 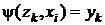 . Таким образом, F-автомат называется асинхронным, если каждое его состояние
. Таким образом, F-автомат называется асинхронным, если каждое его состояние 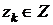 устойчиво.
устойчиво.
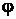 и
и 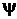 , то с их помощью осуществляются отображения G->Z и G->Y, то говорят, что F= <Z, X, Y,
, то с их помощью осуществляются отображения G->Z и G->Y, то говорят, что F= <Z, X, Y,