
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению задачи 1Содержание книги
Поиск на нашем сайте
Сущность символического метода состоит в том, что гармонической функции тока (напряжения, ЭДС) ставится в соответствие комплексная гармоническая функция:
Для Закон Ома в символической форме имеет вид:
где При последовательном соединении элементов
где При параллельном соединении элементов
Пример решения задачи 1
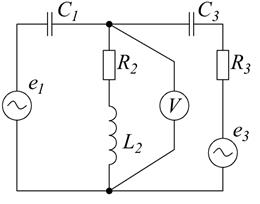
Решить задачу 1 для схемы, представленной на рисунке 2.11, с исходными данными таблицы 2.2.
Таблица 2.2 – Исходные данные для примера решения задачи 1
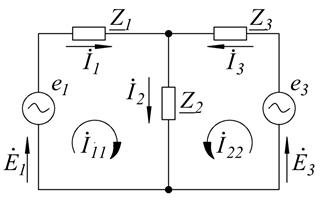
Рисунок 2.11 – Схема электрической цепи для примера решения задачи 1 Преобразуем исходную схему, заменив сопротивления ветвей полными комплексными сопротивлениями (рисунок 2.12). Вольтметр в схеме не учитываем из-за большой величины сопротивления. Произвольно задаёмся направлением комплексов токов в ветвях и ЭДС источников.
Рисунок 2.12 – Преобразованная схема электрической цепи для примера решения задачи 1
Найдем полные сопротивления в ветвях:
Подставив полученные значения, получим значения полных сопротивлений в ветвях в комплексной форме:
Решим задачу методом непосредственного применения законов Кирхгофа. Число узлов схемы k = 2; число ветвей n =3. Число уравнений по первому закону Кирхгофа k – 1 = 2 – 1 = 1. Число уравнений по второму закону Кирхгофа n – (k – 1) = 3 – (2 – 1) = 2. Составим уравнения для верхнего узла схемы и контуров:
где
Подставив числовые значения, получим
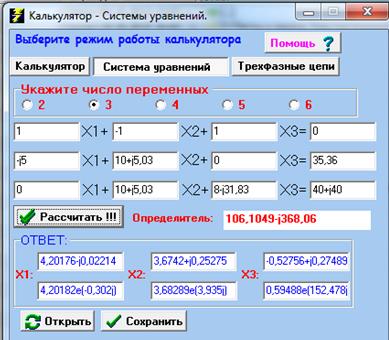
Для решения системы уравнений воспользуемся программой «Калькулятор» (рисунок 2.13).
Рисунок 2.13 – Результат решения системы уравнений для определения токов методом непосредственного применения законов Кирхгофа в программе «Калькулятор»
Полученные токи
Решим задачу методом контурных токов. Составим систему уравнений по второму закону Кирхгофа (см. рисунок 2.12):
Подставив числовые значения в систему, получим:
Выразим
Подставим
Токи, полученные двумя методами решения, совпадают. Решение задачи проверяем, составив уравнение баланса мощностей источников и нагрузки
Комплексные мощности источников ЭДС
где
Комплексные мощности нагрузки:
Баланс мощностей выполняется. Определяем показания вольтметра (рисунок 2.14):
Вольтметр показывает значение UV = 41,21 В.
Рисунок 2.14 – Схема для определения показания вольтметра
Находим напряжения на участках цепи:
Запишем уравнение мгновенного значения тока для третьей ветви
где
Тогда
График (волновая диаграмма тока) i 3 приведен на рисунке 2.15.
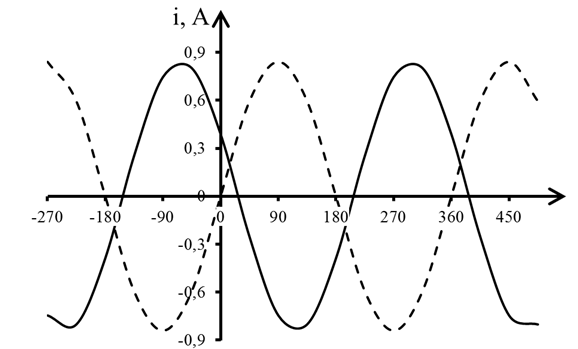
Рисунок 2.15 – Волновая диаграмма тока i3
Составим модель схемы в среде Multisim (рисунок 2.16).
Рисунок 2.16 – Модель схемы к задаче 1 в среде Multisim
Результаты решения задачи 2 представлены в таблице 2.3.
Таблица 2.3 – Результаты решения задачи 2
Результаты, полученные разными методами решения задачи, совпадают.
Задача 2. Для электрической цепи, схема которой приведена на рисунках 2.17 – 2.26, по заданным параметрам в таблице 2.4 и линейному напряжению, выполнить следующее: – определить фазные и линейные токи, ток в нейтральном проводе (для четырехпроводной сети); – определить активную, реактивную и полную мощности, потребляемые схемой; – составить модель схемы в среде Multisim, определить фазные и линейные токи; – построить векторную диаграмму токов и напряжений на комплексной плоскости. Задачу решить для двух случаев: 1) ключ К замкнут; 2) ключ К разомкнут.
Таблица 2.4 – Исходные данные к задаче 2
Окончание таблицы 2.4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.116.234 (0.008 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

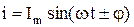 ;
; 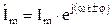 .
.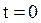 комплексное амплитудное значение тока
комплексное амплитудное значение тока 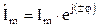 , а комплекс действующего значения тока
, а комплекс действующего значения тока 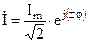 . Аналогично
. Аналогично 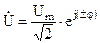 .
.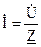 ,
,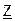 – комплекс полного сопротивления цепи.
– комплекс полного сопротивления цепи.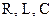
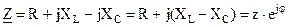 ,
,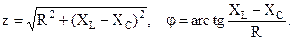
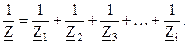
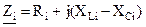 ;
; 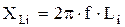 ;
; 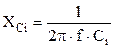 ;
;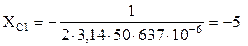 Ом;
Ом;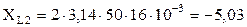 Ом;
Ом; Ом.
Ом.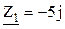 Ом;
Ом;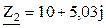 Ом;
Ом;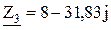 Ом.
Ом.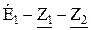 и
и 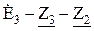 .
.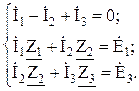
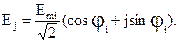
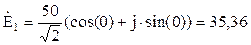 B;
B;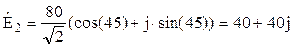 B.
B.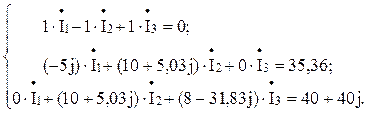
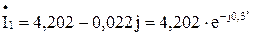 A;
A;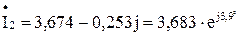 A;
A;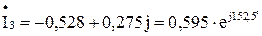 A.
A.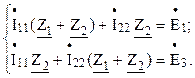
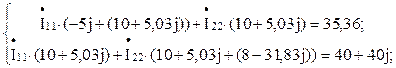
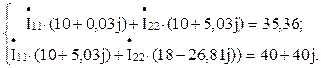
 из второго уравнения:
из второго уравнения: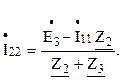
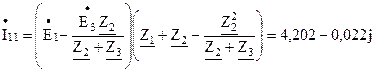 A;
A;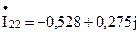 A;
A;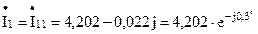 A;
A;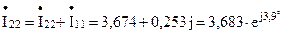 A;
A;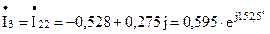 A.
A.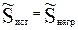 .
.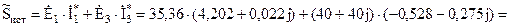
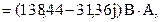
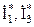 - комплексные сопряжённые значения токов.
- комплексные сопряжённые значения токов.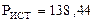 Вт;
Вт; 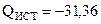 Вар.
Вар.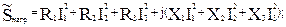
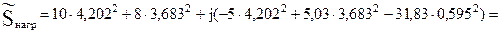
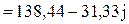 B·A.
B·A.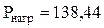 Вт;
Вт; 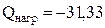 Вар.
Вар.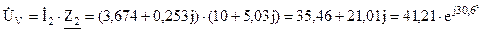 B.
B.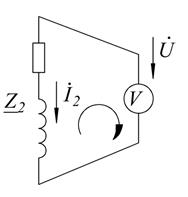
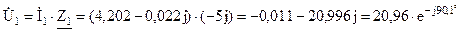 B;
B;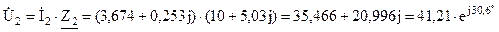 B;
B;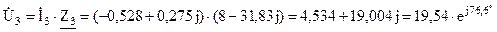 B.
B.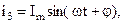
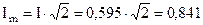 А;
А;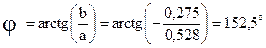
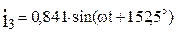


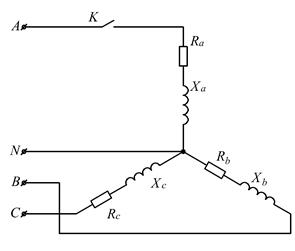 Рисунок 2.17
Рисунок 2.17
 Рисунок 2.18
Рисунок 2.18
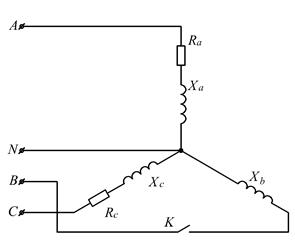 Рисунок 2.19
Рисунок 2.19
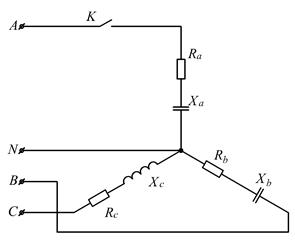 Рисунок 2.20
Рисунок 2.20
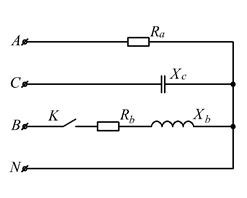 Рисунок 2.21
Рисунок 2.21
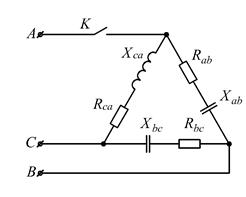 Рисунок 2.22
Рисунок 2.22
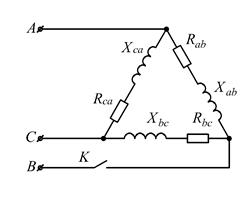 Рисунок 2.23
Рисунок 2.23
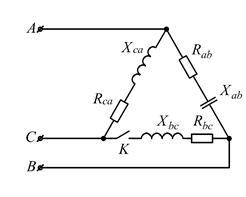 Рисунок 2.24
Рисунок 2.24
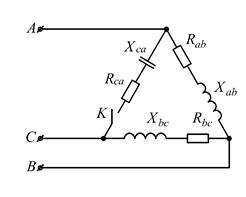 Рисунок 2.25
Рисунок 2.25
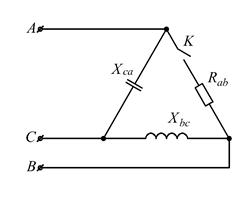 Рисунок 2.26
Рисунок 2.26



