Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электротехника и электроникаСодержание книги
Поиск на нашем сайте ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Методические рекомендации к самостоятельной работе студентов Специальности 1-36 01 06 «Оборудование и технология сварочного производства» дневной и заочной форм обучения Часть 1
Могилев 2016 УДК 621.3 ББК 32.85 Э 45 Рекомендовано к изданию учебно-методическим отделом Белорусско-Российского университета
Одобрено кафедрой «Электротехника и электроника» «____» мая 2016 г., протокол № 11
Составители: канд. техн. наук, доц. С.В. Болотов ассистент И.В. Курлович
Рецензент д-р физ-мат. наук, проф. А.В. Хомченко
Методические рекомендации предназначены для выполнения самостоятельной работы студентами дневной и заочной формы обучения специальности 1-36 01 06 «Оборудование и технология сварочного производства».
Учебно-методическое издание
ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА Часть 1
Ответственный за выпуск Ф. М. Трухачёв Технический редактор А. А. Подошевко Компьютерная верстка _____________
Подписано в печать . Формат 60х84/16. Бумага офсетная. Гарнитура Таймс. Печать трафаретная. Усл. печ. л. . Уч.-изд. л. . Тираж 56 экз. Заказ № .
Издатель и полиграфическое исполнение Государственное учреждение высшего профессионального образования «Белорусско-Российский университет» Свидетельство о государственной регистрации издателя, изготовителя, распространителя печатных изданий № 1/156 от 24.01.2014 Пр. Мира, 43, 212000, г. Могилев,
© ГУ ВПО «Белорусско-Российский университет», 2016 Введение
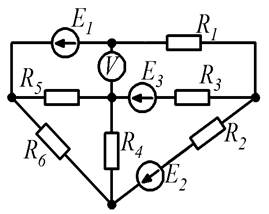
Выполнение самостоятельной работы по дисциплине «Электротехника и электроника» способствует более глубокому усвоению теоретических закономерностей и получению практических навыков расчёта и моделирования работы электрических цепей постоянного и переменного токов в среде NI Multisim. Работы выполняют на страницах формата А4. На первой странице (обложке или титульном листе) обязательно следует указать следующую информацию: название и порядковый номер расчётно-графического задания, вариант, свою фамилию, инициалы и учебную группу, фамилию преподавателя, год. Работы без выше перечисленных сведений на проверку не принимаются. На последующих страницах приводят условие задания, расчётную схему, размещают решение задания с краткими пояснениями. Модели электрических цепей и результаты моделирования вставляют в текст работы. Схемы и диаграммы выполняют в графическом редакторе в соответствии с требованиями ГОСТ 2.723-68, ГОСТ 2.747-68. Следует также изучить соответствующие разделы рекомендуемой литературы и методических указаний по курсу. Задания выполняют и представляют на проверку в установленные учебным графиком сроки. Вариант задания выдаётся преподавателем. Параметры расчетной схемы выбираются по таблицам. Расчётно-графические задания № 1 «Расчёт электрических цепей постоянного тока» и № 2 «Расчёт электрических цепей переменного тока» (задачи 1 и 2) выполняются в 5-м семестре студентами дневной формы обучения. 1 Расчётно-графическое задание № 1. Расчёт электрических цепей постоянного тока Задача. Для электрических схем, соответствующих номеру варианта и изображенных на рисунках 1.1 – 1.10 (номер рисунка указан в таблице 1.1), выполнить следующее: – составить и решить численным методом систему уравнений, необходимых для определения токов в ветвях по первому и второму законам Кирхгофа; – составить баланс мощностей для заданной схемы; – найти все токи в ветвях, пользуясь методом контурных токов; – проверить правильность решения, применив метод двух узлов, предварительно упростив схему, заменив треугольник сопротивлений R 4, R 5, R 6 эквивалентной звездой; – определить показание вольтметра; – построить потенциальную диаграмму для внешнего контура; – составить модель схемы в среде Multisim, определить токи в ветвях и показание вольтметра.
Таблица 1.1 – Исходные данные к задаче
Окончание таблицы 1.1
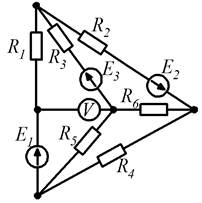
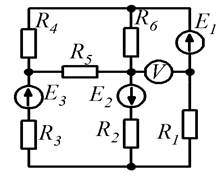
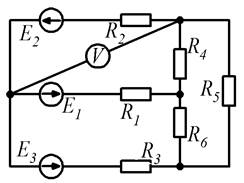
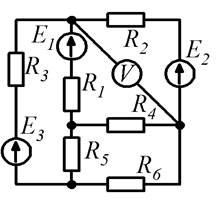
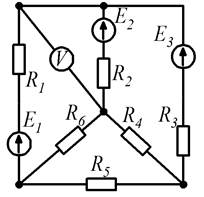
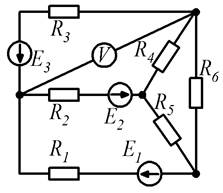
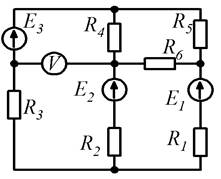
Рисунок 1.1 Рисунок 1.2
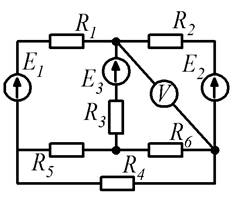
Рисунок 1.3 Рисунок 1.4
Рисунок 1.5 Рисунок 1.6
Рисунок 1.7 Рисунок 1.8
Рисунок 1.9 Рисунок 1.10 Метод контурных токов вытекает из метода, основанного на непосредственном применении законов Кирхгофа. Уравнения по методу контурных токов составляют по второму закону Кирхгофа введением так называемых контурных токов. Количество уравнений, составленных по методу контурных токов, n – (k – 1).
Направления контурных токов выбираются произвольно. При составлении уравнений положительными принимаются ЭДС, совпадающие с направлениями контурных токов. Решая систему уравнений, определим значение контурных токов. Во внешних ветвях контурные токи будут являться истинными токами. Токи в смежных ветвях определяют по первому закону Кирхгофа. Пример решения задачи
Пример решения задачи 1
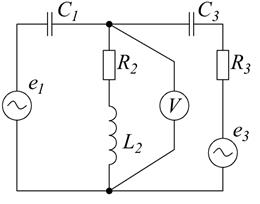
Решить задачу 1 для схемы, представленной на рисунке 2.11, с исходными данными таблицы 2.2.
Таблица 2.2 – Исходные данные для примера решения задачи 1
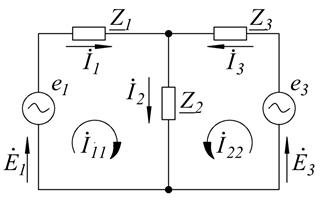
Рисунок 2.11 – Схема электрической цепи для примера решения задачи 1 Преобразуем исходную схему, заменив сопротивления ветвей полными комплексными сопротивлениями (рисунок 2.12). Вольтметр в схеме не учитываем из-за большой величины сопротивления. Произвольно задаёмся направлением комплексов токов в ветвях и ЭДС источников.
Рисунок 2.12 – Преобразованная схема электрической цепи для примера решения задачи 1
Найдем полные сопротивления в ветвях:
Подставив полученные значения, получим значения полных сопротивлений в ветвях в комплексной форме:
Решим задачу методом непосредственного применения законов Кирхгофа. Число узлов схемы k = 2; число ветвей n =3. Число уравнений по первому закону Кирхгофа k – 1 = 2 – 1 = 1. Число уравнений по второму закону Кирхгофа n – (k – 1) = 3 – (2 – 1) = 2. Составим уравнения для верхнего узла схемы и контуров:
где
Подставив числовые значения, получим
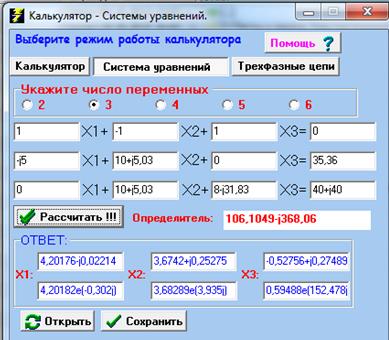
Для решения системы уравнений воспользуемся программой «Калькулятор» (рисунок 2.13).
Рисунок 2.13 – Результат решения системы уравнений для определения токов методом непосредственного применения законов Кирхгофа в программе «Калькулятор»
Полученные токи
Решим задачу методом контурных токов. Составим систему уравнений по второму закону Кирхгофа (см. рисунок 2.12):
Подставив числовые значения в систему, получим:
Выразим
Подставим
Токи, полученные двумя методами решения, совпадают. Решение задачи проверяем, составив уравнение баланса мощностей источников и нагрузки
Комплексные мощности источников ЭДС
где
Комплексные мощности нагрузки:
Баланс мощностей выполняется. Определяем показания вольтметра (рисунок 2.14):
Вольтметр показывает значение UV = 41,21 В.
Рисунок 2.14 – Схема для определения показания вольтметра
Находим напряжения на участках цепи:
Запишем уравнение мгновенного значения тока для третьей ветви
где
Тогда
График (волновая диаграмма тока) i 3 приведен на рисунке 2.15.
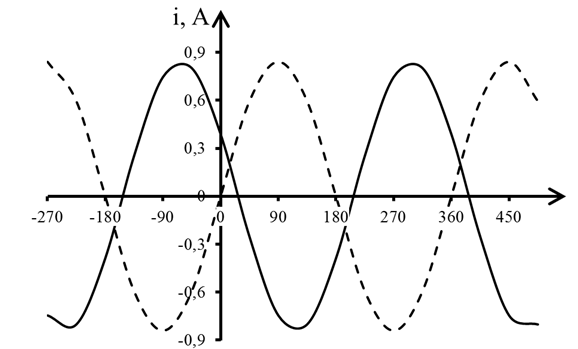
Рисунок 2.15 – Волновая диаграмма тока i3
Составим модель схемы в среде Multisim (рисунок 2.16).
Рисунок 2.16 – Модель схемы к задаче 1 в среде Multisim
Результаты решения задачи 2 представлены в таблице 2.3.
Таблица 2.3 – Результаты решения задачи 2
Результаты, полученные разными методами решения задачи, совпадают.
Задача 2. Для электрической цепи, схема которой приведена на рисунках 2.17 – 2.26, по заданным параметрам в таблице 2.4 и линейному напряжению, выполнить следующее: – определить фазные и линейные токи, ток в нейтральном проводе (для четырехпроводной сети); – определить активную, реактивную и полную мощности, потребляемые схемой; – составить модель схемы в среде Multisim, определить фазные и линейные токи; – построить векторную диаграмму токов и напряжений на комплексной плоскости. Задачу решить для двух случаев: 1) ключ К замкнут; 2) ключ К разомкнут.
Таблица 2.4 – Исходные данные к задаче 2
Окончание таблицы 2.4
Пример решения задачи 2
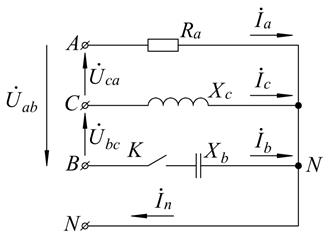
Решить задачу 2 для схемы, представленной на рисунке 2.28, с исходными данными таблицы 2.5.
Рисунок 2.28 – Схема электрической цепи Таблица 2.5 – Исходные данные к задаче 2
Найдем полные сопротивления:
Несимметричная нагрузка. Рассмотрим случай, когда ключ замкнут. Фазные напряжения для схемы определяются по заданному линейному напряжению.
Линейные токи равны фазным. Фазные токи определяем по закону Ома, используя значения полученных фазных напряжений и заданных сопротивлений соответствующих фаз:
Находим ток в нейтральном проводе:
Полная мощность может быть определена в комплексной форме:
Активная мощность, потребляемая схемой,
Реактивная мощность
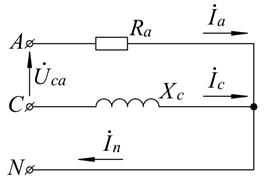
Рассмотрим случай, когда ключ разомкнут (обрыв фазы b, рисунок 2.29):
Ток в фазе b отсутствует.
Рисунок 2.29 – Схема электрической цепи для разомкнутого ключа
Ток в нейтральном проводе
Полная мощность может быть определена в комплексной форме:
Активная и реактивная мощности
Координаты для построения временных диаграмм (рисунки 2.30 и 2.31): - ключ замкнут
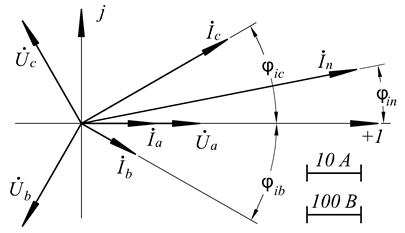
Рисунок 2.30 – Векторная диаграмма токов и напряжений при замкнутом ключе
- ключ разомкнут
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


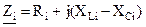 ;
; 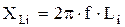 ;
; 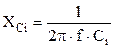 ;
;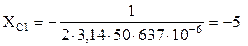 Ом;
Ом;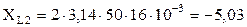 Ом;
Ом; Ом.
Ом.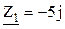 Ом;
Ом;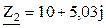 Ом;
Ом;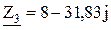 Ом.
Ом.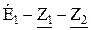 и
и 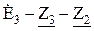 .
.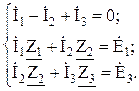
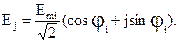
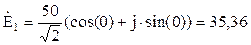 B;
B;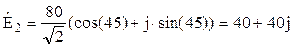 B.
B.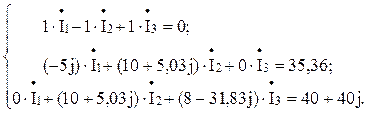
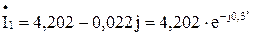 A;
A;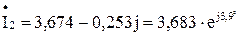 A;
A;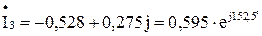 A.
A.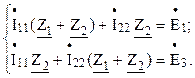
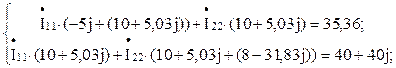
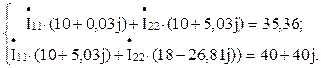
 из второго уравнения:
из второго уравнения: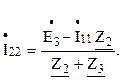
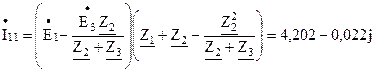 A;
A;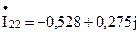 A;
A;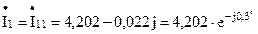 A;
A;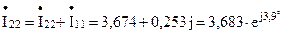 A;
A;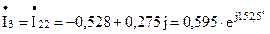 A.
A.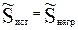 .
.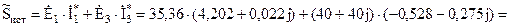
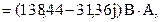
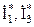 - комплексные сопряжённые значения токов.
- комплексные сопряжённые значения токов.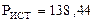 Вт;
Вт; 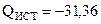 Вар.
Вар.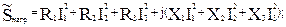
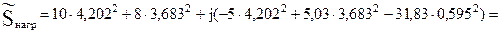
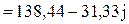 B·A.
B·A.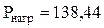 Вт;
Вт; 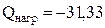 Вар.
Вар.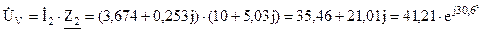 B.
B.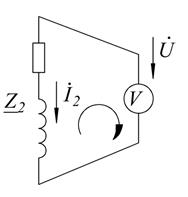
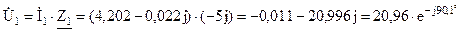 B;
B;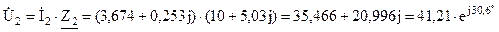 B;
B;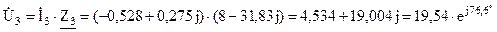 B.
B.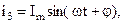
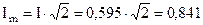 А;
А;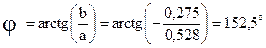
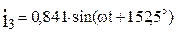


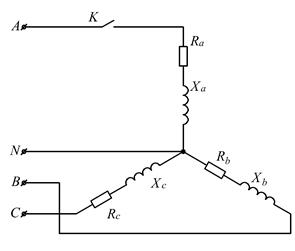 Рисунок 2.17
Рисунок 2.17
 Рисунок 2.18
Рисунок 2.18
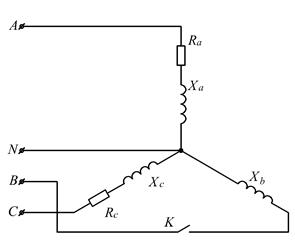 Рисунок 2.19
Рисунок 2.19
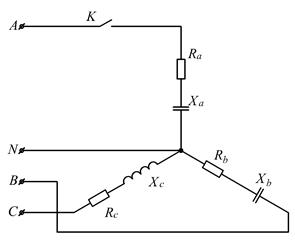 Рисунок 2.20
Рисунок 2.20
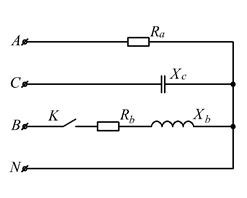 Рисунок 2.21
Рисунок 2.21
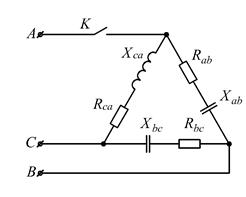 Рисунок 2.22
Рисунок 2.22
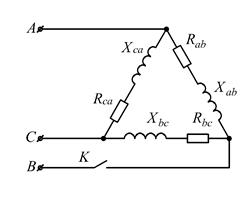 Рисунок 2.23
Рисунок 2.23
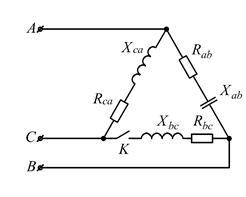 Рисунок 2.24
Рисунок 2.24
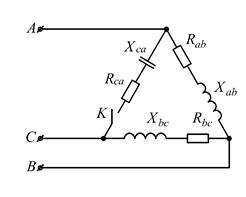 Рисунок 2.25
Рисунок 2.25
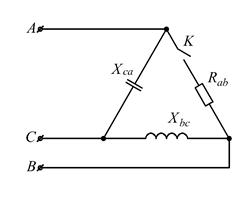 Рисунок 2.26
Рисунок 2.26
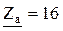 Ом;
Ом; 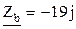 Ом;
Ом; 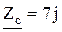 Ом.
Ом.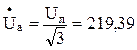 B;
B;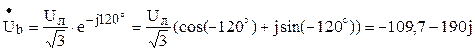 B;
B;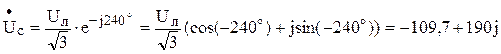 B.
B.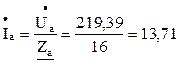 A;
A;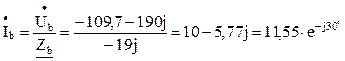 A;
A; A.
A.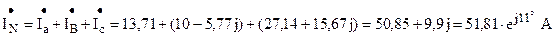
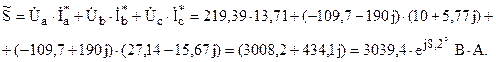
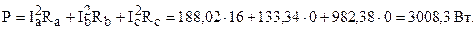
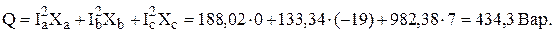
 ;
; 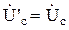 ;
; 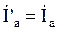 ;
; 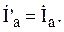
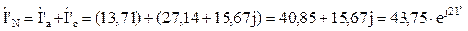 А.
А.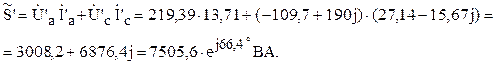
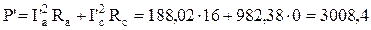 Вт;
Вт;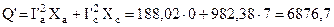 Вар.
Вар.