
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Имитационное моделирование законов распределенияСодержание книги
Поиск на нашем сайте
Имитационное моделирование
Разработка и внедрение производственных систем (ПС) в действующее производство связано с большими капитальными вложениями, поэтому производят моделирование работы ПС. Главная проблема при этом состоит выборе ее структуры, включая тип оборудования и организацию производственных функций. С ростом сложности ПС применение моделирования становится неизбежным. Создание натурных моделей в металле, как и опытной партии обходится слишком дорого и значительно удлиняет сроки внедрения достижений науки и техники. Аналитические методы исследования сложных систем используют различные упрощающие допущения и позволяют получать результат в виде формул лишь для достаточно простых задач. Преимущество аналитического моделирования – возможность исследовать влияние параметров и структуры на эффективность системы и большая приспособленность для поиска оптимальных решений. Включение в состав производственных показателей таких переменных, как отказы и простои оборудования, меняющаяся номенклатура деталей, меняющаяся загрузка станков делают невозможным аналитическое описание процессов (сложно алгоритмизировать). Наиболее эффективным методом исследования сложных систем является имитационное моделирование, при котором моделируются последовательность случайных событий: поступление деталей, их обработка, формирование сборочных комплектов, образование брака и т.п. Имитационное моделирование как точное воспроизведение последовательности реальных событий позволяет учесть особенности сложного процесса и управления системой в целом. ИМ осуществляется при помощи специально разработанного программного обеспечения и реализуется на ЭВМ. Информация о работе производственных систем включает все необходимые данные для оценки оптимальной структуры, загруженности оборудования и времени производства. Имитационные модели используются для количественного и качественного анализа и получения информации о работе производственных систем, использовании станков, величины производственных заделов, объеме выпуска и других показателей в зависимости от разнообразия деталей, времени обработки и наладки, размера партии деталей и других параметров.
С развитием вычислительной техники применение ИМ становится все более эффективным. Наибольший эффект достигается при одновременном использовании аналитических моделей (например, для расчета отдельных параметров) и методов ИМ (для более детального расчета параметров). Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить основные закономерности. Любые уточнения могут быть получены с помощью имитационных моделей. В производственных системах имитационное моделирование помогает оптимизировать многие параметры без создания опытных образцов. Моделирование работы производственных систем является инструментом управления производства. Имитационное моделирование позволяет принимать конструктивные решения, как при модернизации производства, так и при разработке производственных систем. ИМ отличается от натурного эксперимента тем, что его можно полностью осуществлять на ЭВМ. Имитационное моделирование – это программное обеспечение, с помощью которого при вводе информации о начальных условиях задачи можно получить ее решение в численном виде. Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализов взаимосвязей между ее элементами. Результаты исследования имитационной модели представляют собой оценки характеристик системы. Имитационное моделирование рассматривается как статистический эксперимент. В отличие от математической модели, результаты, получаемые в имитационном моделировании, представляют собой наблюдения, которые необходимо еще статистически обработать (статистические модели). Особенно успешно ИМ применяется при оперативном планировании в расчетах максимальной загрузки оборудования и возможной себестоимости продукции. Имитационное моделирование используется при проектировании и эксплуатации производственных систем. При проектировании производственных систем имитационное моделирование позволяет отвечать на вопросы: - сколько и какого типа требуется станков, - что произойдет при изменении номенклатуры деталей, - какую ЭВМ необходимо иметь, - какую информацию необходимо накапливать и т.д.
При эксплуатации имитационное моделирование позволяет отвечать на вопросы: - каковы показатели ПС при различных объемах выпускаемой продукции, - какие имеются резервы, - какой график выпуска продукции оптимален, - какой вид транспортировки (конвейерный или адресуемый) оптимален, - что произойдет при отказе одного из станков, - каков уровень производительности труда и т.д. Имитационное моделирование производства может выполняться как при планировании, так и в реальном времени процесса производства. В первом случае имеется возможность прогнозирования процесса, во втором – можно вести расчет показателей состояния системы на каждый момент производственного цикла. Если имитационная модель связана с информационной системой, то можно оптимизировать управление, как отдельной системы, так и подразделения или предприятия в целом. Могут создаваться имитационные модели специального назначения для изучения отдельных частей системы, например, оптимизация организации инструментального хозяйства, выбор схемы смены инструмента на станках или порядок работы роботов. При ИМ не следует детализировать процесс. Имитационное моделирование используется при решении задач двух типов: 1. Теоретические задачи (вычисление площадей, интегралов, решение дифференциальных уравнений или систем линейных уравнений); 2. Практические задачи (производственно-технические, экономические, социальные, военные). Положительные свойства (+): имитационные модели позволяют учесть большое число факторов и формировать любые законы распределения. Недостатки (–): громоздкость, трудоемкость, плохая обозримость, большой расход машинного времени, трудность поиска оптимальных решений, большое число реализаций, необходимое для нахождения искомых параметров с приемлемой точностью.
Метод Монте-Карло
Метод, используемый для решения задач имитационного моделирования, известен давно и называется метод Монте-Карло. Идея метода состоит в использовании выборок. Процесс получения выборок требует, чтобы решаемая задача была описана вероятностным распределением, в соответствии с которым осуществляются выборки. Вместо того чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений) производится «розыгрыш» случайного явления с помощью специально организованной процедуры. В действительности конкретное осуществление (реализация) случайного процесса складывается каждый раз по-иному; так же и в результате имитационного моделирования («розыгрыша») получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Это множество реализаций можно использовать как статистический материал, который может быть обработан обычными методами математической статистики. Методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он может быть тогда, когда процедура розыгрыша проще аналитического расчета. Датой рождения метода считается 1949 г., когда американские ученые Н. Метрополис и С. Улан опубликовали статью с его изложением. Название метода связано с городом Монте-Карло, где играют в рулетку – одно из простейших устройств для получения случайных чисел, на использовании которых основан этот метод.
0 1 2 … 9 1 2 3 4
0,1 0,1 0,1... 0,1 0,5 0,25 0,125 0,125 Сложно получать случайные числа на реальном физическом приборе, так как они вырабатываются с распределением несколько отличающимся от идеального (пример, лототрон).
По равновероятному закону В имитационных моделях выборка, соответствующая любому вероятностному распределению, производится на основе использования равномерно распределенных случайных чисел из интервала [0, 1] Существует три основных способа формирования случайных чисел: табличный, аппаратный, алгоритмический. При табличном способе случайные числа заранее формируются с помощью специального механического (простейший вид – рулетка) или электронного устройства. Последовательность таких чисел затем записывается в память ЭВМ. Данный способ не получил распространения вследствие трудоемкости заготовки таблиц, необходимости в большом объеме памяти, отводимой под эти таблицы, больших затратах времени в процессе моделирования при размещении этой таблицы во внешнем накопителе. При аппаратном способе последовательность случайных чисел вырабатывается отдельным электронным узлом-генератором случайных чисел (ГСЧ), в котором используется задающий элемент — источник шумов, которые затем усиливаются, селектируются на определенном уровне с последующим формированием последовательности случайных импульсов с равновероятным появлением единичных импульсов на любом месте случайной последовательности. Недостатками данного метода являются необходимость аппаратного усложнения ЭВМ и невозможность повторного получения идентичных последователей, что важно при отладке программ и проведении сравнительных расчетов. Для обеспечения возможности неоднократного воспроизведения одинаковых последовательностей используются генераторы псевдослучайных чисел (ГПСЧ). Приставка «псевдо» означает, что числа фактически случайными не являются, но практически ведут себя как случайные; все значения от 0 до 1 встречаются в среднем одинаково часто и связь между последовательными значениями получаемых чисел практически отсутствует. Кроме того процесс генерации числовой последовательности начинается с некоторого исходного случайного числа. Наибольшее распространение имеет алгоритмический способ получения случайных чисел. В настоящее время в основном используется так называемый конгруэнтный алгоритм Лемера, по которому составляется стандартная подпрограмма получения случайных чисел. Во всех выпускаемых в настоящее время ЭВМ, включая микроЭВМ, заложена стандартная подпрограмма R A NDOM (случайный), сокращенно записываемая R A ND или R N D, по которой вырабатывается случайное число, равномерно распределенное в интервале 0 < ri < 1.
(Таблицы случайных чисел, в том числе файл в ЭВМ) Запуск генератора в ЭВМ, либо с постоянного числа – для отладки программы, либо со случайного – для исследований.
По требуемому закону
Генерация случайных чисел, подчиняющихся различным законам, основана на генерации в ЭВМравномерно распределенных случайных чисел и последующего преобразования этих чисел. Для этого используются методы: преобразования (например, для экспоненциального, нормального, логарифмически нормального распределений), композиции (гамма–функция, распределения Пуассона, биномиальное, нормальное), отбраковки (бета–функция) и метод обратной функции (один из наиболее распространенных методов преобразования).
Метод обратной функции
Случайная величина Х описывается интегральной F (x) и дифференциальной f (x) функциями распределения. Зная одну изэтих функций, можно предсказать поведение случайной величины, так как функции связаны между собой соотношениями:
Условие формирования непрерывной случайной величины Х по заданному закону распределения: поскольку Ri = F (х i), то необходимо выполнить преобразование
Х i = F –1(Ri),
где Ri — равномерно распределенное случайное число; F –1 – функция, обратная по отношению к распределению случайной величины Х.
Использование метода обратной функции для расчета случайной величины требует сравнительно больших затрат машинного времени, так как связано с численным решением не поддающегося аналитическому расчету интеграла. Имеются табулированные значения интеграла для нормированной величины S = (х – m x)/s x, по которым, записав таблицу в память ЭВМ можно находить случайные величины, распределенные по требуемому закону. На основании данного выражения можно моделировать случайные числа с требуемым законом распределения. В требуемом диапазоне Если случайная величина распределена в диапазоне от a до b, то моделирование ее значений будет производиться по выражениям:
1. Для равновероятностного закона: Плотность вероятности:
где Ri в интервале [0, 1]. Погрешность отсчета при измерениях. 2. Д ля нормального закона распределения: Плотность вероятности:
где или, пара нормально распределенных случайных чисел полученных методом преобразования (метод Бокса – Миллера) со средним, равным 0 и дисперсией равной 1:
где R 1 и R 2 – пара случайных величин в интервале [0, 1]. В Excel имеются функции: НОРМОБР – при заданных x, m и s. НОРМСТОБР – при заданном x, m =0 и s=1. Распределение размеров в партии деталей, погрешность измерения. 3. Распределение Релея Плотность вероятности:
где Погрешности формы деталей: овальность, конусообразность, седлообразность, бочкообразность. 4. Логарифмически нормальное распределение (логнормальное) Размер заказов, длина очереди, распределение доходов, имущества.
где m=е m – медиана, m – матожидание.
Генерирование случайных чисел:
5. Распределение модуля разности Погрешность взаимного расположения поверхностей, непараллельность осей, плоскостей, изгиб оси.
где m = | m 1 – m 2|.
Генерирование случайных чисел:
6. Экспоненциальное распределение
где
Промежутки времени безотказной работы (время жизни).
Имитационное моделирование необходимо рассматривать как статистический эксперимент, поэтому накопленные данные следует статистически обработать и при необходимости провести корреляционный и регрессионный анализ, т. е. установить зависимости между переменными.
Имитационное моделирование
Разработка и внедрение производственных систем (ПС) в действующее производство связано с большими капитальными вложениями, поэтому производят моделирование работы ПС. Главная проблема при этом состоит выборе ее структуры, включая тип оборудования и организацию производственных функций. С ростом сложности ПС применение моделирования становится неизбежным. Создание натурных моделей в металле, как и опытной партии обходится слишком дорого и значительно удлиняет сроки внедрения достижений науки и техники. Аналитические методы исследования сложных систем используют различные упрощающие допущения и позволяют получать результат в виде формул лишь для достаточно простых задач. Преимущество аналитического моделирования – возможность исследовать влияние параметров и структуры на эффективность системы и большая приспособленность для поиска оптимальных решений. Включение в состав производственных показателей таких переменных, как отказы и простои оборудования, меняющаяся номенклатура деталей, меняющаяся загрузка станков делают невозможным аналитическое описание процессов (сложно алгоритмизировать). Наиболее эффективным методом исследования сложных систем является имитационное моделирование, при котором моделируются последовательность случайных событий: поступление деталей, их обработка, формирование сборочных комплектов, образование брака и т.п. Имитационное моделирование как точное воспроизведение последовательности реальных событий позволяет учесть особенности сложного процесса и управления системой в целом. ИМ осуществляется при помощи специально разработанного программного обеспечения и реализуется на ЭВМ. Информация о работе производственных систем включает все необходимые данные для оценки оптимальной структуры, загруженности оборудования и времени производства. Имитационные модели используются для количественного и качественного анализа и получения информации о работе производственных систем, использовании станков, величины производственных заделов, объеме выпуска и других показателей в зависимости от разнообразия деталей, времени обработки и наладки, размера партии деталей и других параметров. С развитием вычислительной техники применение ИМ становится все более эффективным. Наибольший эффект достигается при одновременном использовании аналитических моделей (например, для расчета отдельных параметров) и методов ИМ (для более детального расчета параметров). Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить основные закономерности. Любые уточнения могут быть получены с помощью имитационных моделей. В производственных системах имитационное моделирование помогает оптимизировать многие параметры без создания опытных образцов. Моделирование работы производственных систем является инструментом управления производства. Имитационное моделирование позволяет принимать конструктивные решения, как при модернизации производства, так и при разработке производственных систем. ИМ отличается от натурного эксперимента тем, что его можно полностью осуществлять на ЭВМ. Имитационное моделирование – это программное обеспечение, с помощью которого при вводе информации о начальных условиях задачи можно получить ее решение в численном виде. Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализов взаимосвязей между ее элементами. Результаты исследования имитационной модели представляют собой оценки характеристик системы. Имитационное моделирование рассматривается как статистический эксперимент. В отличие от математической модели, результаты, получаемые в имитационном моделировании, представляют собой наблюдения, которые необходимо еще статистически обработать (статистические модели). Особенно успешно ИМ применяется при оперативном планировании в расчетах максимальной загрузки оборудования и возможной себестоимости продукции. Имитационное моделирование используется при проектировании и эксплуатации производственных систем. При проектировании производственных систем имитационное моделирование позволяет отвечать на вопросы: - сколько и какого типа требуется станков, - что произойдет при изменении номенклатуры деталей, - какую ЭВМ необходимо иметь, - какую информацию необходимо накапливать и т.д. При эксплуатации имитационное моделирование позволяет отвечать на вопросы: - каковы показатели ПС при различных объемах выпускаемой продукции, - какие имеются резервы, - какой график выпуска продукции оптимален, - какой вид транспортировки (конвейерный или адресуемый) оптимален, - что произойдет при отказе одного из станков, - каков уровень производительности труда и т.д. Имитационное моделирование производства может выполняться как при планировании, так и в реальном времени процесса производства. В первом случае имеется возможность прогнозирования процесса, во втором – можно вести расчет показателей состояния системы на каждый момент производственного цикла. Если имитационная модель связана с информационной системой, то можно оптимизировать управление, как отдельной системы, так и подразделения или предприятия в целом. Могут создаваться имитационные модели специального назначения для изучения отдельных частей системы, например, оптимизация организации инструментального хозяйства, выбор схемы смены инструмента на станках или порядок работы роботов. При ИМ не следует детализировать процесс. Имитационное моделирование используется при решении задач двух типов: 1. Теоретические задачи (вычисление площадей, интегралов, решение дифференциальных уравнений или систем линейных уравнений); 2. Практические задачи (производственно-технические, экономические, социальные, военные). Положительные свойства (+): имитационные модели позволяют учесть большое число факторов и формировать любые законы распределения. Недостатки (–): громоздкость, трудоемкость, плохая обозримость, большой расход машинного времени, трудность поиска оптимальных решений, большое число реализаций, необходимое для нахождения искомых параметров с приемлемой точностью.
Имитационное моделирование законов распределения
Имитационное моделирование основано на воспроизведении изучаемого явления на ЭВМ с помощью теоретических зависимостей с непосредственным моделированием случайных факторов, анализом взаимосвязей между элементами и на статистической обработке результатов. Основой метода имитационного моделирования является воспроизведение случайных величин с заданным распределением. Для получения выборок используется метод Монте–Карло.
Метод Монте-Карло
Метод, используемый для решения задач имитационного моделирования, известен давно и называется метод Монте-Карло. Идея метода состоит в использовании выборок. Процесс получения выборок требует, чтобы решаемая задача была описана вероятностным распределением, в соответствии с которым осуществляются выборки. Вместо того чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений) производится «розыгрыш» случайного явления с помощью специально организованной процедуры. В действительности конкретное осуществление (реализация) случайного процесса складывается каждый раз по-иному; так же и в результате имитационного моделирования («розыгрыша») получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Это множество реализаций можно использовать как статистический материал, который может быть обработан обычными методами математической статистики. Методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он может быть тогда, когда процедура розыгрыша проще аналитического расчета. Датой рождения метода считается 1949 г., когда американские ученые Н. Метрополис и С. Улан опубликовали статью с его изложением. Название метода связано с городом Монте-Карло, где играют в рулетку – одно из простейших устройств для получения случайных чисел, на использовании которых основан этот метод.
0 1 2 … 9 1 2 3 4 0,1 0,1 0,1... 0,1 0,5 0,25 0,125 0,125 Сложно получать случайные числа на реальном физическом приборе, так как они вырабатываются с распределением несколько отличающимся от идеального (пример, лототрон).
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.014 с.) |


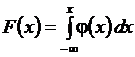 , j (x)= F ¢ (x)
, j (x)= F ¢ (x)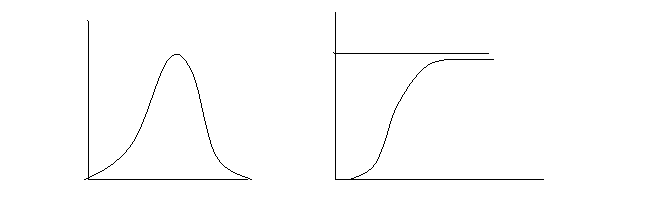
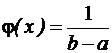 ,
, 
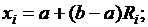 [ a, b ],
[ a, b ],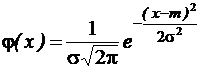
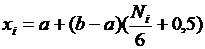
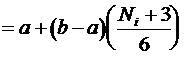 [ a, b ],
[ a, b ],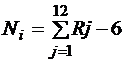 [-3, 3]
[-3, 3]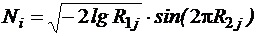 [-3, 3]
[-3, 3] [-3, 3],
[-3, 3],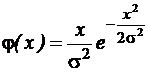
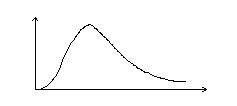
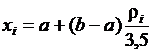 [ a, b ],
[ a, b ], [0; 3,5] при a=0,95
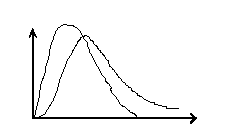
[0; 3,5] при a=0,95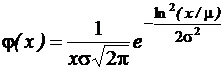 ,
,
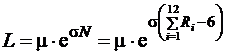 , [0; 5] при a=0,95.
, [0; 5] при a=0,95.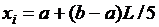 при m =1, s=1.
при m =1, s=1.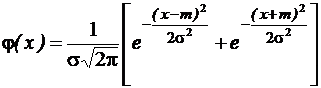
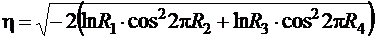 , [0; 3,5]
, [0; 3,5]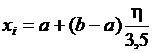
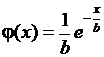
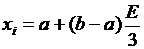 [ a, b ],
[ a, b ],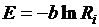 [0; 3] при a=0,95
[0; 3] при a=0,95


