
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближение равной вероятности символов в текстеСодержание книги
Поиск на нашем сайте
Если допустить, что все символы алфавита в любом тексте появляются с одинаковой частотой, то информационный вес всех символов будет одинаковым. Пусть N — мощность алфавита. Тогда доля любого символа в тексте составляет 1/ N -ю часть текста. По определению вероятности эта величина равна вероятности появления символа в каждой позиции текста:
Согласно формуле Шеннона, количество информации, которое несет символ, вычисляется следующим образом:
Следовательно, информационный вес символа (i) и мощность алфавита (N) связаны между собой по формуле Хартли:
Зная информационный вес одного символа (i) и размер текста, выраженный количеством символов (K), можно вычислить информационный объем текста по формуле:
Эта формула есть частный вариант формулы (5), в случае, когда все символы имеют одинаковый информационный вес. Из формулы (6) следует, что при N = 2 (двоичный алфавит) информационный вес одного символа равен 1 биту. С позиции алфавитного подхода к измерению информации 1 бит — это информационный вес символа из двоичного алфавита. Более крупной единицей измерения информации является байт. 1 байт — это информационный вес символа из алфавита мощностью 256. Поскольку 256 = 28, то из формулы Хартли следует связь между битом и байтом: 2i = 256 = 28 Отсюда: i = 8 бит = 1 байт. Для представления текстов, хранимых и обрабатываемых в компьютере, чаще всего используется алфавит мощностью 256 символов. Следовательно, 1 символ такого текста “весит” 1 байт.
Пример 2.1. Для записи текста используются только строчные буквы русского алфавита и “пробел” для разделения слов. Какой информационный объем имеет текст, состоящий из 2000 символов (одна печатная страница)? В русском алфавите 33 буквы. Сократив его на две буквы (например, “ё” и “й”) и введя символ пробела, получаем очень удобное число символов — 32. Используя приближение равной вероятности символов, запишем формулу Хартли: 2i = 32 = 25 Отсюда: i =5 бит — информационный вес каждого символа русского алфавита. Тогда информационный объем всего текста равен: L = 2000*5 = 10 000 бит
Пример 2.2. Вычислить информационный объем текста размером в 2000 символов, в записи которого использован алфавит компьютерного представления текстов мощностью 256. В данном алфавите информационный вес каждого символа равен: i=log2256=8 бит = 1 байт Следовательно, информационный объем текста равен L=2000 * 1 байт = 2000 байт Если пересчитать информационный объем текста килобайты, то получим: L=2000 байт = 2000/1024 Пример 2.3. Объем сообщения, содержащего 1024 символов, составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение?
Переведем информационный объем сообщения из мегабайтов в биты. Для этого данную величину умножим дважды на 1024 (получим байты) и один раз — на 8: L = 1/512 * 1024 * 1024 * 8 = 16384 бита Поскольку такой объем информации несут 1024 символа (К), то на один символ приходится: i = L/ K= 16384/1024 = 16 бит
Отсюда следует, что размер (мощность) использованного алфавита равен N = 216 = 65536 символов.
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

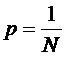
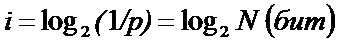
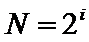
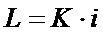
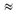 1,9531 Кб
1,9531 Кб


