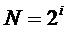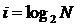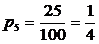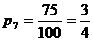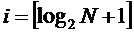Содержательный подход к измерению количества информации

 

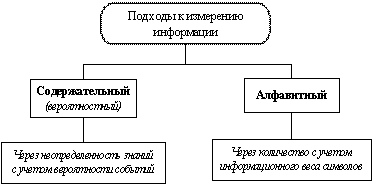
К измерению информации применяют 2 подхода: содержательный и алфавитный.

 

 

Для содержательного подхода необходимо понять неопределенность знаний, вероятностные события.  С позиции содержательного подхода к измерению информации решается вопрос о количестве информации в сообщении, получаемом человеком.

 

Неопределенность знаний

 

Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. 

Неопределенность знания о результате некоторого события – это число возможных вариантов события (бросания монеты, кубика, вытаскивания жребия).

 

Вы, бросаете монету, загадывая, что выпадет: орел или решка? Есть два варианта результата бросания монеты. Причем, ни один из этих вариантов не имеет преимущества перед другим. В таком случае они равновероятны. Неопределенность знаний о результате равна двум. Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знаний о результате бросания равна шести.

Сообщение уменьшающее неопределенность знаний в два раза, несет для него 1 бит информации.

 

Вернемся к примеру с монетой. После того, как вы бросили монету и посмотрели на нее, вы получили зрительное сообщение, что выпал, например, орел. Произошло одно из двух возможных событий. Неопределенность знаний уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили один бит информации.

 

Равновероятные события

 

Рассматривается следующая ситуация:

1) человек получает сообщение о некотором событии; при этом заранее известна неопределенность знания человека об ожидаемом событии. Неопределенность знания может быть выражена либо числом возможных вариантов события, либо вероятностью ожидаемых вариантов события;

2) в результате получения сообщения неопределенность знания снимается: из некоторого возможного количества вариантов оказался выбранным один;

3) по формуле вычисляется количество информации в полученном сообщении, выраженное в битах.

 

Формула, используемая для вычисления количества информации, зависит от ситуаций, которых может быть две:

1. Все возможные варианты события равновероятны. Их число конечно и равно N.

2. Вероятности (p) возможных вариантов события разные и они заранее известны:

{p_i}, i = 1.. N, такие что p₁+ p₂+… p_N =1

 

Здесь по-прежнему N — число возможных вариантов события.

 

Вводя понятие вероятности, следует сообщить, что вероятность некоторого события - это величина, которая может принимать значения от нуля до единицы. Вероятность невозможного события равна нулю (например: “завтра Солнце не взойдет над горизонтом”), вероятность достоверного события равна единице (например: “Завтра солнце взойдет над горизонтом”).

Вероятность некоторого события определяется путем многократных наблюдений (измерений, испытаний). Такие измерения называют статистическими. И чем большее количество измерений выполнено, тем точнее определяется вероятность события.

Математическое определение вероятности звучит так: вероятность равна отношению числа исходов, благоприятствующих данному событию, к общему числу равновозможных исходов.

 

События равновероятны, если ни одно из них не имеет преимущества перед другими.

 

Если обозначить буквой i количество информации в сообщении о том, что произошло одно из N равновероятных событий, то величины i и N связаны между собой формулой Хартли:

(1)

 

Величина i измеряется в битах. Отсюда следует вывод:

 

1 бит — это количество информации в сообщении об одном из двух равновероятных событий.

 

Формула Хартли — это показательное уравнение. Если i — неизвестная величина, то решением уравнения (1) будет:

(2)

Формулы (1) и (2) тождественны друг другу. Иногда в литературе формулой Хартли называют формулу (2).

Пример 1.1. Сколько информации содержит сообщение о том, что из колоды карт достали даму пик?

В колоде 32 карты. В перемешанной колоде выпадение любой карты — равновероятные события. Если i — количество информации в сообщении о том, что выпала конкретная карта (например, дама пик), то из уравнения Хартли i = 5 бит:  2ⁱ = 32 = 2⁵

Пример 1.2. Сколько информации содержит сообщение о выпадении грани с числом 3 на шестигранном игральном кубике?

 

Считая выпадение любой грани событием равновероятным, запишем формулу Хартли: 2ⁱ = 6. Отсюда: i = log₂6 = 2,58496 бит.

 

Можно решить задачу и так:

Из уравнения Хартли: 2ⁱ = 6. Поскольку 2² < 6 < 2³, следовательно,   2 < i < 3.  

При содержательном подходе количество информации может быть выражено дробной величиной.

 

Пример 1.3. На автобусной остановке останавливаются два маршрута автобусов: №5 и №7. Ученику дано задание: определить, сколько информации содержит сообщение о том, что к остановке подошел автобус №5, и сколько информации в сообщении о том, что подошел автобус №7.

 

Ученик провел исследование. В течение всего рабочего дня он подсчитал, что к остановке автобусы подходили 100 раз. Из них — 25 раз подходил автобус №5 и 75 раз подходил автобус №7.

Сделав предположение, что с такой же частотой автобусы ходят и в другие дни, ученик вычислил вероятность появления на остановке автобуса №5:

и вероятность появления автобуса №7:

 

Количество информации в сообщении об автобусе №5 вычисляем:

i ₅ = log₂4 = 2 бита.

Количество информации в сообщении об автобусе № 7 равно:

 

i ₇ =log₂(4/3)=log₂4–log₂3=2–1,58496=0,41504 бита.

 

Обратите внимание на следующий качественный вывод: чем вероятность события меньше, тем больше количество информации в сообщении о нем. Количество информации о достоверном событии равно нулю. Например, сообщение “Завтра наступит утро” является достоверным и его вероятность равна единице. Из формулы (3) следует: 2ⁱ = 1

Отсюда, i = 0 бит.

 

Если число N не является целой степенью числа 2, то число log₂N не является целым. Тогда проводят округление в большую сторону по формуле:

(5)

 

Приведем таблицу для логарифмов по основанию 2:

 

N	i	N	i	N	i	N	i
1	0,00000	17	4,08746	33	5,04439	49	5,61471
2	1,00000	18	4,16993	34	5,08746	50	5,64386
3	1,58496	19	4,24793	35	5,12928	51	5,67243
4	2,00000	20	4,32193	36	5,16993	52	5,70044
5	2,32193	21	4,39232	37	5,20945	53	5,72792
6	2,58496	22	4,45943	38	5,24793	54	5,75489
7	2,80735	23	4,52356	39	5,28540	55	5,78136
8	3,00000	24	4,58496	40	5,32193	56	5,80735
9	3,16993	25	4,64386	41	5,35755	57	5,83289
10	3,32193	26	4,70044	42	5,39232	58	5,85798
11	3,45943	27	4,75489	43	5,42626	59	5,88264
12	3,58496	28	4,80735	44	5,45943	60	5,90689
13	3,70044	29	4,85798	45	5,49185	61	5,93074
14	3,80735	30	4,90689	46	5,52356	62	5,95420
15	3,90689	31	4,95420	47	5,55459	63	5,97728
16	4,00000	32	5,00000	48	5,58496	64	6,00000

При решении задач, если N не является степенью числа 2, то его можно заменить на N', где N' – ближайшая к N степень числа 2 такая, что N'>N.