Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смесь гаусовских распределений
Плотность распределения НСВ ξ представляет собой смесь двух гаусовских распределений N 1 (μ 1, σ 1 2) и N 2 (μ 2 σ 2 2) (модель засорений Тьюки-Хьюбера с уровнем засорений ε Осуществить n реализаций моделирования CB ξ и провести графический анализ результатов моделирования при следующих значениях параметров: 1) μ1=μ2=0;, σ2=ασ1,α=1/2,2,4, σ1=1; ε=0.05,0.45,n=20,50,100,500 2) μ1=0,μ2=6;, σ2=ασ1,α=1/2,1,2, σ1=1; ε=0.05,0.45,n=20,50,100,500 Глава 6. Метод Монте-Карло и его применения Общая схема метода Монте-Карло
Метод Монте-Карло – это численный метод исследования математических моделей сложных систем, основанный на моделировании случайных элементов и последующем статистическом анализе результатов моделирования. Метод Монте-Карло реализуется с помощью следующих шагов: 1. подбирают такую случайную величину ξ, что выполняются условия где a-скалярная величина, приближенное значение, которое надо найти; 2. моделируют n независимых реализаций случайной величины ξ: 3. по случайной выборке Точность вычислений характеризуют либо с помощью доверительного интервала, определяемого интервалом вероятность выполнения которого приблизительно равна β; (например при где численный множитель 0,6745 является решением уравнений т.е. одинаково вероятны ошибки, больше, чем Вычисление определенного интеграла методом Монте-Карло
Рассмотрим задачу приближенного вычисления интеграла
где
Заметим, что схема вычислений как многомерных, так и одномерных интегралов, абсолютно аналогична. Пусть η – произвольная случайная величина с плотностью распределения вероятностей Предполагается только, что существуют моменты случайных величин, встречающиеся ниже. Рассмотрим случайную величину, являющуюся функциональным преобразованием случайной величины η.
Можно показать, что
Пример. Вычислить интеграл Решение. Выберем случайный вектор
Ее можно рассматривать как совместную плотность распределения двух независимых экспоненциально распределенных случайных величин Пусть в результате моделирования независимых компонент случайного вектора
#include <fstream.h> #include <math.h> #include <stdlib.h> #include <limits.h> #include <time.h> // basic variate double bv(double*a, double*b, double*c,int m,int n){ int i, tmp; double result = c; for =(i =0;i<n,i ++) resalt +=b[i]*a[i]; tmp=(int)(resalt/m); resalt -=((double)tmp)*((double)m); for(i=1;I<n;i++) a[i-1]=a[i]; a[n-1]=resalt; return resalt/m; } // exponential variate p(x)=lexp(-lx),x>=0 double ev(double 1,double a) { return –log(1-a)/1; } double avg(double*a,int n){ double s=0; for(int i=0;i<n;i++) s+=*(a+i); return s/n; } double var(double*a,int n){ double s=0,s=2; for(int i=0;i<n;i++){ s+=a[i]; s2+=a[i]*a[i]; } return(s2-s*s/n)/(n-1); } void main() { int i,j; const int n=1000; double a[2][n];//two pseudorandom sequences double b[2][n];//coefficients double c[2]; //increment int m[2] //modules
//initial values srand((unsigned) time (NULL)); for(j=0;j<2;j++){ m[j] =RAND_MAX-rand(); for(i=0;i<n;i++){ a[j][i]=rand()%m[j]; b[j][i]=rand(); } c[j]=rand(); }
//computation double tmp; double*A =new double[n]; double*x =new double[n]; double*y =new double[n]; ofstream out(“integral.txt”); for(j=1;j<=5;j++){ for(i=0;i<n;i++){ do{ do{ x[i]=ev(2,dv(a[0],b[0],c[0],m[0],n)); y[i]=ev(0.5,dv(a[1],b[1],c[1],m[1],n)); }while(x[i]-y[i]==0); tmp= 1+log(pow(y[i]-x[i],2)); }while(tmp<0); A[i]=sqrt(tmp); } out<<avg(A,n)<<”\n”; out<<var(A,n)<<”\n”; out<<0.6745*sqrt(var(A,n)/n)<<”\n\n”; } }
Некоторые статистические результаты моделирования: Запустим программу по 5 раз для различных значений n.
Вычислить интеграл аналитически не удается. Полученное с помощью программы Mathematica4.1 точное значение интеграла равно 1.4221. Как видим, полученные в результате выполнения программы значения интеграла близки к точному, однако точность в данном случае невысока. Точность возрастает с увеличением объема выборки. Вероятная ошибка уменьшается.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.107 (0.018 с.) |

 ,
,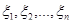 ;
;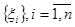 , строят выборочную оценку
, строят выборочную оценку 
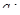



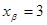 ), либо с помощью так называемой вероятной ошибки метода Монте-Карло:
), либо с помощью так называемой вероятной ошибки метода Монте-Карло:
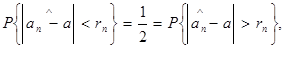
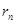 и ошибки, меньшие, чем
и ошибки, меньшие, чем 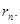
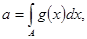
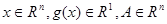 - подмножество из
- подмножество из  При n=1 имеем определенный интеграл вида
При n=1 имеем определенный интеграл вида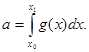
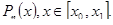
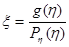
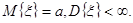 Поэтому в качестве приближенного значения интеграла можно использовать статистическую оценку
Поэтому в качестве приближенного значения интеграла можно использовать статистическую оценку 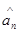 , построенную в выборке из n независимых случайных величин
, построенную в выборке из n независимых случайных величин 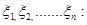

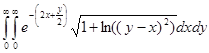 Методом Монте-Карло.
Методом Монте-Карло. с плотностью распределения
с плотностью распределения 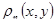 , равной
, равной 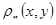 =
= 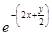 . Для
. Для  выполняются условия
выполняются условия ,
, 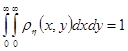 .
.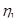 и
и 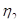 с плотностями распределения
с плотностями распределения 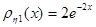 и
и 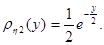 Тогда
Тогда 
 получена случайная выборка
получена случайная выборка 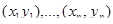 . Согласно методу Монте-Карло в качестве приближенного значения интеграла следует использовать статистику
. Согласно методу Монте-Карло в качестве приближенного значения интеграла следует использовать статистику