Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение системы алгебраических уравнений методом Монте-Карло
Моделирование цепей Маркова оказывается естественным образом связанным с решением большого числа задач, и, в первую очередь, с решением систем линейных алгебраических уравнений. Рассмотрим простейшую вычислительную схему для решения линейных алгебраических уравнений, которая была впервые предложена Дж. Нейманом и С. Уламом [12]. Пусть система алгебраических уравнений задана в виде
где Предположим, что наибольшее по модулю характеристическое число матрицы А меньше единицы, так что сходиться метод последовательных приближений
Достаточным условием для того, чтобы все характеристические числа матрицы А лежали внутри единичного круга на комплексной плоскости, то есть, чтобы Если положить, что
– точное решение системы (4.3.1) Рассмотрим задачу о вычислении скалярного произведения Мы будем связывать с системой (4.3.1) и вектором h некоторую фиксированную цепь Маркова из множества цепей, определяемых парой
для которых выполнены условия:
Положим
Зададимся некоторым целым N, и будем рассматривать траектории цепи Маркова длины N > 0. Объект, переходы которого описываются цепью Маркова, условимся называть частицей и считать, что эта частица изменяет свои состояния (движется в соответствии с траекторией цепи). Движущейся частице приписывается "вес"
Введем случайную величину
Используя формулу умножения вероятностей, найдем
Тогда математическое ожидание СВ
Подставим выражения для
Используя определение произведения матриц получим
т.е.
Из (4.3.3) и (4.3.14) следует, что при Итак, доказана следующая теорема. Теорема 4.3.1. Если все характеристические числа матрицы А по абсолютной величине меньше единицы, то математическое ожидание случайной величины
Для получения приближенного значения
Вы.16заций цепи Маркова:)ие ()чения иницы, то математическое ожидание случайной величинычисляем вдоль цепей (4.3.16) веса
Приближенное значение для
Пример. Решить систему линейных алгебраических уравнений с использованием метода Монте-Карло:
Решение: Приведем систему к виду, при котором применим метод Монте-Карло:
Таким образом, система имеет вид:
Все собственные значения матрицы Ф по модулю меньше 1 и можно применять метод Монте-Карло. Определим некоторый вектор h следующим образом: h= Моделируем вспомогательную цепь Маркова:
Вектор вероятностей начальных состояний цепи Маркова: Матрица переходных вероятностей имеет вид: Каждому состоянию цепи Маркова приписываем веса, которые вычисляются по формулам:
Теперь можем построить СВ
где
Данный алгоритм реализован на языке С++.
Текст программы:
#include <iostream.h> #include <stdlib.h> #include <time.h>
void main(){ int n; //Размерность системы float x=0,y=0; //Решение системы float **a; //Исходная матрица float *f; //Правая часть системы float *h; float *pi; //Вектор нач. вероятностей цепи Маркова float **p; //Матрица переходных состояний цепи Маркова int N; //Длина цепи Маркова int *i; //Цепь Маркова float *Q; //Веса состояний цепи Маркова float *ksi; //СВ int m; //Количество реализаций цепи Маркова float alpha; //БСВ n=2; a=new float*[n]; for(int k=0;k<n;k++) a[k]=new float[n]; f=new float[n]; h=new float[n]; pi=new float[n]; p=new float*[n]; for(k=0;k<n;k++) p[k]=new float[n]; N=1000; i=new int[N+1]; Q=new float[N+1]; m=10000; ksi=new float[m]; for(int j=0;j<m;j++) ksi[j]=0; a[0][0]=-0.1; a[0][1]=0.8; a[1][0]=0.4; a[1][1]=-0.1; f[0]=0.1; f[1]=-0.2; h[1]=1; h[0]=0; pi[1]=0.5; pi[0]=0.5; p[0][0]=0.5; p[0][1]=0.5; p[1][0]=0.5; p[1][1]=0.5; //Моделируем m цепей Маркова длины N for(j=0;j<m;j++) { alpha=rand()/float(RAND_MAX); if(alpha<pi[0]) i[0]=0; //реализуется 1-е состояние else i[0]=1; //реализуется 2-е состояние for(k=1;k<=N;k++) { alpha=rand()/float(RAND_MAX); if(alpha<0.5) i[k]=0; else i[k]=1; } //Вычисляем веса цепи Маркова if(pi[i[0]]>0) Q[0]=h[i[0]]/pi[i[0]]; else Q[0]=0; for(k=1;k<=N;k++) { if(p[i[k-1]][i[k]]>0) Q[k]=Q[k-1]*a[i[k-1]][i[k]]/p[i[k-1]][i[k]]; else Q[k]=0; } for(k=0;k<=N;k++) ksi[j]=ksi[j]+Q[k]*f[i[k]]; } for(k=0;k<m;k++) x=x+ksi[k]; x=x/m; cout << x; }
Результат работы программы:
x=-0.0559199 y=-0.199699
Точное решение системы:
x=-5/89≈0.056179775 y=-18/89≈0.202247191
Задания
Вычислить интегралы:
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.66.151 (0.039 с.) |
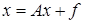 (4.3.1)
(4.3.1)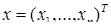 – вектор-столбец неизвестных,
– вектор-столбец неизвестных, 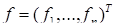 – вектор правых частей и
– вектор правых частей и 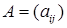 ,
, 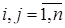 – матрица системы.
– матрица системы.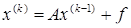 ,
, 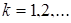 (4.3.2)
(4.3.2)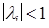 ,
, 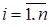 , может служить неравенство
, может служить неравенство 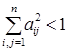 или неравенство
или неравенство 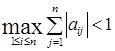 .
.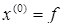 , то
, то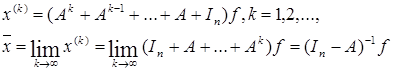 (4.3.3)
(4.3.3)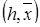 , где h – заданный вектор.
, где h – заданный вектор.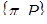 :
: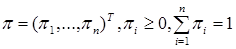 , (4.3.4)
, (4.3.4)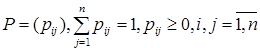 , (4.3.5)
, (4.3.5)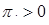 , если
, если 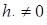 ,
, 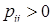 , если
, если 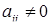 ;
; 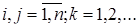 (4.3.6)
(4.3.6)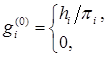
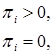
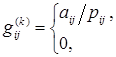
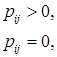 (4.3.7)
(4.3.7)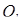 , который изменяется при движении ее по траектории
, который изменяется при движении ее по траектории 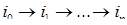 следующим образом. В начальный момент, когда она находится в состоянии
следующим образом. В начальный момент, когда она находится в состоянии 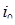 , частица имеет вес
, частица имеет вес 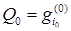 ,при переходе из состояния
,при переходе из состояния 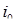 в состояние
в состояние 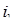 ее вес становиться равным
ее вес становиться равным 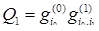 и т.д., т.е.
и т.д., т.е.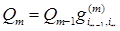 . (4.3.8)
. (4.3.8)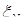 , определенную на траекториях Марковской цепи длины N
, определенную на траекториях Марковской цепи длины N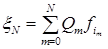 , (4.3.9)
, (4.3.9)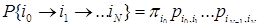 (4.3.10)
(4.3.10)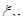 равно
равно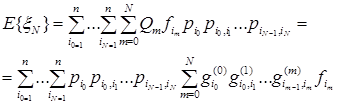 (4.3.11)
(4.3.11)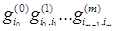 , определяемые по формуле (4.3.7), получим
, определяемые по формуле (4.3.7), получим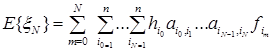 (4.3.12)
(4.3.12)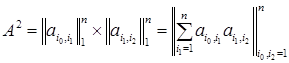 , (4.3.13)
, (4.3.13)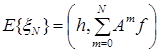 . (4.3.14)
. (4.3.14)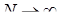
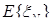 стремиться к
стремиться к 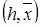 .
.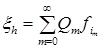 равно
равно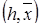 . (4.3.15)
. (4.3.15)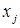 – j -й компоненты вектора
– j -й компоненты вектора 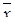 (решения системы (4.3.1)) выбираем в качестве h единичный вектор
(решения системы (4.3.1)) выбираем в качестве h единичный вектор 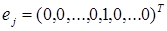 , в котором лишь на j -м месте стоит единица. Тогда скалярное произведение (4.3.15) равно
, в котором лишь на j -м месте стоит единица. Тогда скалярное произведение (4.3.15) равно 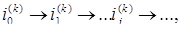
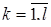 ,
, 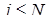 . (4.3.16)
. (4.3.16) согласно формуле (4.3.8), тогда
согласно формуле (4.3.8), тогда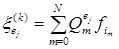 . (4.3.17)
. (4.3.17)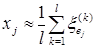 . (4.3.18)
. (4.3.18)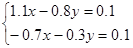
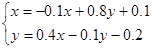
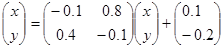
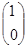 для вычисления x, h=
для вычисления x, h= 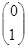 для вычисления y.
для вычисления y.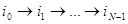 , где
, где 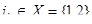 .
.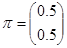 .
. .
.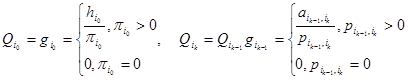
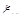 по формуле:
по формуле: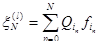 ,
,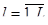 - номер реализации цепи Маркова. Тогда приближенное решение вычисляется по формуле:
- номер реализации цепи Маркова. Тогда приближенное решение вычисляется по формуле: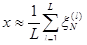 или
или 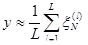 в зависимости от вектора h.
в зависимости от вектора h.