
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.Стр 1 из 13Следующая ⇒
ГРУПИ Література: 1. А. Г. Курош, курс высшей алгебры, М 2. Б. Л. Вандер Ванден, Современная алгебра, ч. І, М.-Л, ОГИЗ, 1947г. 3. Л. А. Калужин, Введение в общую алгебру, М, Наука, 1973г. Як зазначалось в курсі алгебри першого семестру, основним об’єктом вивчення в алгебрі є алгебраїчні структури. Під алгебраїчною структурою розуміють множину М, на якій задана деяка система алгебраїчних операцій, які задовольняють деякі умови-аксіоми структури. Як відомо, алгебраїчні операції діляться на два типи:внутрішні закони композиції і зовнішні закони композиції. В даному розділі під алгебраїчною операцією, означеною на множині М, розумітимемо скрізь бінарний внутрішній закон композиції на М, тобто відображення прямого добутку М× М в М. Раніше ми ознайомилися з однією важливою алгебраїчною структурою — полем. Структура поля означається шляхом задання на множині двох алгебраїчних операцій — додавання і множення, які задовольнють відомим дев’яти аксіомам. Але найпростіші серед алгебраїчних структур є структури, які означаються однією алгебраїчною операцією. До вивчення таких структур ми зараз і приступимо. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп. І. АЛГЕБРАЇЧНІ C ТРУКТУРИ З ОДНІЄЮ ОПЕРАЦІЄЮ. Озн ачення 1. Не порожня множина М, на якій означена одна алгебраїчна операція, називається групоїдом. Алгебраїчну операцію що визначає групоїд, будемо найчастіше називати множенням і вживати мультиплікативний запис a × b. Підкреслимо, що операція, яка визначає групоїд М, повинна бути скрізь означеною на множині М, тобто
Щоб відзначити, що групоїд визначається двома компонентами — множиною М і алгебраїчною операцією, означеною на ній, — часом для групоїда вживають таке позначення: Приклади. 1. Множина всіх векторів трьохвимірного простору R, є групоїдом, якщо під алгебраїчною розуміти операцію знаходження векторного добутку двох векторів. 2. Множина всіх підстановок n -го степеня з операцією множення підстановок утворює групоїд. 3. Якщо в множині R всіх дійсних чисел розглядати тільки операцію додавання чисел, то сукупність
Як відомо, операція знаходження векторного добутку двох векторів є асоціативною і комутативною, відносно неї не існує нейтрального елемента. Операція множення підстановок є асоціативною, але не є комутативною, відносно неї існує одиничний елемент і для кожної підстановки — обернена. Операція додавання дійсних чисел є асоціативною і комутативною, відносно неї існує нульовий елемент і для кожного числа — протилежне. Як бачимо, в деяких групоїдах алгебраїчна операція насправді задовольняє тим чи іншим умовам. Це дає можливість прокласифікувати групоїд в залежності від того, яким умовам задовольняє алгебраїчна операція групоїду. Ми зупинимось тільки на двох класах групоїдах — півгрупах і групах. Півгрупа — це групоїд, алгебраїчна операція якого є асоціативною. Група — це півгрупа, в якій існує одиничний елемент і для кожного елемента — обернений. Зараз дамо детальніші означення цих об’єктів і вивчимо їх деякі властивості. ІІ. ПІВГРУПА. Означення 2. Непорожня множина М, на якій означена одна алгебраїчна операція, яка є асоціативною, називається півгрупою. Приклади. 1. Множина всіх підстановок n -го степеня з операцією множення підстановок утворює півгрупу. 2. Групоїд 3. Множина всіх матриць n -го порядку утворює півгрупу відносно операції множення матриць, бо множення матриць є асоціативним. В цій півгрупі існує одиничний елемент — одинична матриця Е, але не для кожної матриці існує обернена. 4. Сукупність 5. Множина P всіх цілих парних чисел утворює півгрупу відносно операції множення (добуток парних чисел — парне число, множення чисел асоціативне), причому ця півгрупа нейтрального елемента (І) не містить. Наявність асоціативного закону для операції півгрупи М дозволяє однозначно ввести в М поняття добутку 3, 4, …, n елементів. Оскільки
Добуток 4, 5, …, n елементів означимо рекурентно:
…………………………………………………………………………………… Наявність асоціативного закону для операції півгрупи дозволяє в добутках, що містять більше двох співмножників (такі добутки будемо умовно називати складеними), довільно розставляти дужки. Цей факт випливає з такої теореми: Теорема 1. Добуток двох складених добутків дорівнює складеному добутку всіх співмножників, що входять до їх складу, взятих у тому ж порядку, тобто Доведення. Доведення проведемо методом математичної індукції по n. 1. Якщо n =1, то формула (1) прийме вигляд: 2. Припустимо, що формула (1) справедлива для деякого n, треба довести, що вона справедлива для n +1:
Використовуючи означення добутку (m + n)+1 елементів і асоціативність алгебраїчною операції, послідовно матимемо:
Отже, формула (1) справедлива при n, то вона справедлива і при n +1. На підставі принципу математичної індукції можна стверджувати, що формула (1) справедлива при будь-якому n. Наслідок. В складеному добутку можна вільно розставляти дужки. Справді, тому що у формулі (1) послідовно брати m =1, 2, …, n -1, то дістанемо:
В кожній із одержаній дужок можна на підставі теореми 1 знову довільно розставляти дужки, наслідок чого ми одержимо, наприклад, таке: ІІІ.ОЗНАЧЕННЯГРУПИ.ПРИКЛАДИ. НАЙПРОСТІШІВЛАСТИВОСТІ ГРУП. Означення 3. Не порожня множина G називається групою, якщо на ній означена одна алгебраїчна операція, яка задовольняє таким умовам: 1) Алгебраїчна операція асоціативна, тобто 2) в G існує одиничний елемент е такий, що 3) для кожного елемента Якщо алгебраїчна операція, означена в групі, є додатково комутативною, то група називається комутативною або абелевою. Приклади. 1. Система 2. Множина 3. Множина 4. З аналогічних міркувань система 5. Множина 6. Множина
7. Множина Зауважимо, що групи в прикладах 1-4 і в 6 є абелевими, а групи в прикладах 5 і 7 – неабелеві. Зауважимо також, що алгебраїчні операції в конкретних групах є або операціями множення, або операціями додавання. Групи, в яких алгебраїчні операції є множенням називаються мультиплікативними, а групи, в яких алгебраїчні операції є додаванням, є адитивними. З наведених прикладів видно, також, що одні групи мають безліч елементів – нескінченної групи (групи прикладів 1-5), інші мають скінченну кількість елементів – скінченні групи (групи прикладів 6 і 7). Кількість елементів у скінченній групі G називається порядком цієї групи і позначається Or
Легко перевірити, що множина Вправи. I. Дослідити, чи утворює групу: 1) множина N всіх натуральних чисел відносно додавання і відносно множення чисел, 2) множина Q всіх раціональних чисел відносно додавання і відносно множення чисел, 3) множина 4) множина всіх парних підстановок n -ого степеня відносно операції множення підстановок, 5) множина всіх непарних підстановок n -ого степеня відносно операції множення підстановок. II. Скласти таблицю Келі для симетричної групи Відзначимо декілька найпростіших властивостей груп, які безпосередньо випливають з означення аксіоматики групи.
Ця властивість є безпосереднім наслідком теорем, доведених у курсі алгебри першого семестру, про єдиність нейтрального елемента і симметричного елемента в множині з асоціативною алгебраїчною операцією.
Доведення цієї властивості проводиться точно так само, як і доведення відповідної властивості полів.
Доведення. Щоб показати, що елемент Подібно до того, як вводиться степінь з цілим показником для дійсного числа, поняття степеня з цілим показником можна ввести для будь-якого елемента групи. Означення 4. Нехай G – група і n – ціле число. Тоді
Правила дій над степенями елементів групи ті ж, що і над степенями дійсних чисел: 4*. Якщо G – група, то ( Доведення. В залежності від знаків чисел і розглянемо кілька випадків. 1) m ≥ 0, n ≥ 0. Тоді на підставі означення 4 і теореми 1 а m а n = 2) m ≥ 0, n ≤ 0. Тоді n = -| n | і, використовуючи означення 4 і теорему 1, матимемо:
3) m ≤ 0, n ≥ 0. Розглядається аналогічно випадку 2). 4) m ≤ 0, n ≤ 0. Розглядається аналогічно випадку 1). Наслідок. В групі G ( Справді, а n а - n = а n - n = а 0 = е, а- n а n = а – n + n =а0= е. Методом математичної індукції властивість 4 5
Доведення. Розглянемо два випадки. 1) m – довільне, n
2) m – довільне, n <0. Використовуючи означення 4, наслідок з властивості 4
Вправа. Перефразувати властивості 3-5 для адитивних груп. Зауважимо, що при переході до адитивних груп поняття n-ого степеня елемента
Означення 10. Перша рівність означає. Що елемент (-а) b має бути протилежним до а b, тобто, має виконуватись рівність: а b +(-а) b =0. Ця рівність легко випливає із аксіом 6) і 4) та властивості 9: а b + (-а) b = (а+ (-а)) b = 0 b =0. Аналогічно доводиться, що а(- b)=-а b. Справедливість останньої рівності легко виводиться із перших двох (-а)(- b)=-а(- b)=-(-а b)=а b, бо із рівності а+(-а)=0 в аксіомі 4) виходить, що (-а)+а=0, тобто елементом, протилежним до (-а) Означення 11. Якщо ненулевий елемент а Справді, додавання до обох частин рівності а а або в силу властивості a ( Оскільки елемент а не є дільником нуля, то Зауважимо, що скорочувати рівності на дільники нуля не можна. Справді, як легко пересвідчитись, в кільці М
в той час, як
ІІІ. Підкільце. Одним із важливих напрямків в теорії кілець є вивчення кілець підмножин кільця. Серед усіх підмножин кільця особливо виділяються ті підмножини, які самі є кільцями відносно операцій, означених в усьому кільці. Означення. Підмножина К
Наступна теорема дозволяє спростити фактичну перевірку того, чи утворює певна підмножина кільця його підкільце. Теорема 1. Підмножина 1) ( 2) ( 3) ( Доведення. Якщо підмножина Якщо підмножина Із умови 2 випливає,що для всякого а Приклади. 1. Підмножина Р усіх парних цілих чисел є підкільцем кільця Z цілих чисел. Справді, сума, добуток, парних чисел і число, протилежне до парного, є парними. Це означаєщо Р задовольняє умовам теореми 1, значить Р є пілкільцем кільця Z. 2. Множина Р усіх парних неперервних функцій утворює підкільце кільця С усіх неперервних функцій на [-1,1]. Дійсно, для довільних функцій f (x), g (x) (f+g)(x)= f (-x)+ g (-x)= f (x)+ g (x)=(f+g)(x), (fg)(x)= f (-x) g (-x)= f (x) g (x)=(fg)(x), (-f)(-x)= -f (-x)= -f (x)=(-f)(x). Отже, ( Тобто, множина Р на підставі теореми 1, є підкільцем кільця С. 3.Множина D Зауваження. Умова 2) у формулюванні теореми 1 може бути замінена умовою: 2′) ( Справді, якщо умова 2′) виконується, то для всякого елемента b а- b = а +(- b) Навпаки, якщо справджується умова 2′), то ( Бо 0=а-а і значить, належить Закінчемо параграф переліком деяких підкілець довільного підкільця. 1. Множина О={o}, яка складається тільки з одного нульового елемента кільця К, утворює, очевидно, підкільце кільця К. Це підкільце називають нульовим підкільцем К. 2. Кільце К є, очевидно, підкільцем самого себе. Підкільце О і К називають тривіальними підкільцями кільця К, а всі інші підкільця – нетривіальними або властними підкільцями. 3. Якщо Кα – деякі підкільця кільця К, то їх перетин Ко= Дійсно, якщо a Відомо, яку важливу роль в теоремі груп відіграють циклічні підгрупи (а), породжені елементом а. В наступному пункті побудоване підкільце, яке є аналогом циклічної підгрупи. 4. Нехай К - деяке кільце, а - елемент кільця К. Тоді множина Кα усіх можливих сум
де n1, Кα = Щоб показати, що множина Кα - підкільце кільця К, досить перевірити виконання 1.-3. Із теореми 1. В силу асоціативності додавання виконання умови 1. Очевидне, бо скінчених сумах можна довільно розставляти дужкиі, зокрема, їх опускати: (
1.Як відомо, одним із основних понять математики є поняття, функції, відображення. Це поняття вивчається і в математичному аналізі,і в геометрії,і в алгебрі. При вивченні алгебраїчних структур найбільший інтерес становлять ті відображення, які певним способом узгодженні із алгебраїчною структурою, що вивчається. В теорії груп такими відображеннями є гомоморфізми, тобто, такі ж відображення f групи G в групу ( В теорії кілець вивчаються відображення, які аналогічним способом узгоджені з алгебраїчними операціями, означеними в кільці. Такі відображення називаються кільцевими гомоморфізмами. Означення 1. Відображення f кільця К в кільце ( Перша з цих умов означає, що кільцевий гомоморфізм f в груповим гомоморфізмом адитивної групи кільця К в адитивну групу кільця 1. f (o)=0; 2.( Аналогічно, як і випадку груп, гомоморфізм f: K У зв’язку із властивостями 1. i 2. Виникає питання, чи не будуть аналогічні властивості справедливі відносно операцій множення. Виявляється, що будуть, але при деяких обмеженнях на кільця або на відображення f. Сформулюємо їх: 3. Якщо в кільці К існує 1 i f є епіморфізмом кільця К в кільці Справді, внаслідок сур’єктивності відображення f: ( Тоді ( ( Звідси виходить, що елемент f (1) відіграє роль одиниці в кільці 4.Якщо в кільці К існує І, кільце Дісно, ( і з другого боку, f(a)=f(a) f (a) [ f (1)- Оскільки в К нема дільників нуля і а можна підібрати так, щоб а є К ми включаємо тривіальний випадок: ( є таким, що f (1)= f ( Твердження випливає із рівностей: f (a) f ( f ( Для групового гомоморфізму вводять поняття ядрa Kerf і області значень Imf. Аналогічні поняття вводяться і для кільцевого гомоморфізму. Означення 2. Ядром гомоморфізму f: K Ker f ={ Областю знаень або образом гомоморфізму f: K Im f ={ Як відомо, у випадку групового гомоморфізму f: G Приклад. Розглянемо кільце
і кільце
в якому операції задані так:
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.168.172 (0.15 с.) |
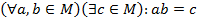
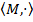 . Як видно з означення, на операцію, яка визначає групоїд, не накладається жодних умов.
. Як видно з означення, на операцію, яка визначає групоїд, не накладається жодних умов. є групоїдом.
є групоїдом. і
і 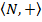 , деN— множина натуральних чисел, утворюють півгрупи, причому в першому випадку нейтральний елемент (І) належить півгрупі, а в другому випадку півгрупа не містить нейтрального елемента (0).
, деN— множина натуральних чисел, утворюють півгрупи, причому в першому випадку нейтральний елемент (І) належить півгрупі, а в другому випадку півгрупа не містить нейтрального елемента (0).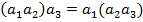 , то добуток
, то добуток  трьох елементів можна прийняти будь–який із елементів
трьох елементів можна прийняти будь–який із елементів  і
і 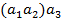 . Приймемо за означенням:
. Приймемо за означенням: 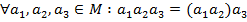
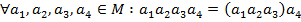

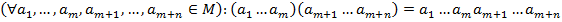 (1)
(1)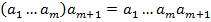 , яка є справедливою згідно прийнятого означення добутку (m +1)-го елемента.
, яка є справедливою згідно прийнятого означення добутку (m +1)-го елемента.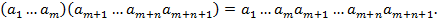
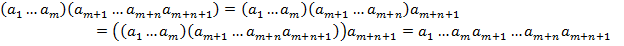
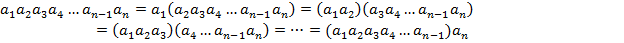
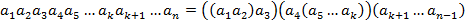
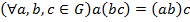 ,
,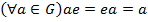 ,
,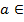 G існує обернений елемент
G існує обернений елемент 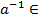 G такий, що a
G такий, що a  =
= 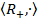 , де
, де 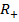 – множина додатних дійсних чисел утворює групу, бо (
– множина додатних дійсних чисел утворює групу, бо (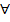 a, b є
a, b є 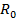 всіх дійсних чисел без нуля теж утворює групу відносно операції множення дійсних чисел. В цьому переконуємось так само як і в прикладі 1.
всіх дійсних чисел без нуля теж утворює групу відносно операції множення дійсних чисел. В цьому переконуємось так само як і в прикладі 1.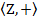 , де Z – множина усіх цілих чисел є групою.
, де Z – множина усіх цілих чисел є групою.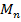 всіх невироджених матриць n -го порядку над полем P утворює групу відносно операції множення матриць. Дійсно (
всіх невироджених матриць n -го порядку над полем P утворює групу відносно операції множення матриць. Дійсно (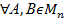 )АВ
)АВ  , бо за теоремою про визначник добутку матриць
, бо за теоремою про визначник добутку матриць 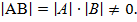 Крім того, 1)Множення матриць асоціативне. 2)В
Крім того, 1)Множення матриць асоціативне. 2)В 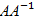 =E виходить
=E виходить 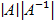 =1 і значить,
=1 і значить, 
 =
=  всіх значень кореня n -ого степеня з 1 утворює групу відносно операції множення комплексних чисел. Справді, якщо
всіх значень кореня n -ого степеня з 1 утворює групу відносно операції множення комплексних чисел. Справді, якщо 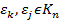 , бо
, бо  =
= 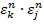 =1. Операція множення задовольняє аксіомам групи: 1) множення комплексних чисел асоціативне, 2) одиниця належить
=1. Операція множення задовольняє аксіомам групи: 1) множення комплексних чисел асоціативне, 2) одиниця належить 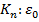 =1, 3) (
=1, 3) (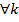 )(
)(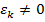 ) і
) і 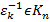 , бо
, бо 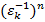 =
= 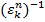 =1.
=1. всіх підстановок n -ого степеня очевидним чином утворює групу відносно операції множення підстановок.
всіх підстановок n -ого степеня очевидним чином утворює групу відносно операції множення підстановок.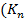 )= n, а в прикладі 7 Or
)= n, а в прикладі 7 Or 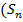 )= n!. В скінченних множинах групову операцію зручно задавати за допомогою таблиць множення, так званих таблиць Келі. В множині
)= n!. В скінченних множинах групову операцію зручно задавати за допомогою таблиць множення, так званих таблиць Келі. В множині 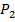 ,що складається з двох поворотів площини навколо нерухомої точки О – точки повороту l на кут
,що складається з двох поворотів площини навколо нерухомої точки О – точки повороту l на кут 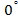 і повороту
і повороту  на кут
на кут  операцією множення задамо такою таблицею Келі:
операцією множення задамо такою таблицею Келі: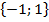 відносно операції множення чисел,
відносно операції множення чисел,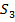 .
.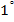 . В усякій групі
. В усякій групі 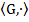 одиничний елемент е є єдиним і для всякого елемента а
одиничний елемент е є єдиним і для всякого елемента а  G обернений елемент
G обернений елемент  . Для всяких елементів а, b
. Для всяких елементів а, b 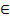 G рівняння ax = b та ay = b мають єдині розв’язки відповідно x =
G рівняння ax = b та ay = b мають єдині розв’язки відповідно x =  . (
. (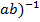 =
= 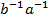 ), тобто елемент обернений до добутку, дорівнює добутку елементів, взятих у зворотному порядку.
), тобто елемент обернений до добутку, дорівнює добутку елементів, взятих у зворотному порядку.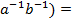 е і
е і 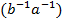 (ab)=е. Покажемо справедливість першої рівності (друга – аналогічно): (ab)(
(ab)=е. Покажемо справедливість першої рівності (друга – аналогічно): (ab)( 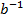 )
) 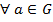 ,
, 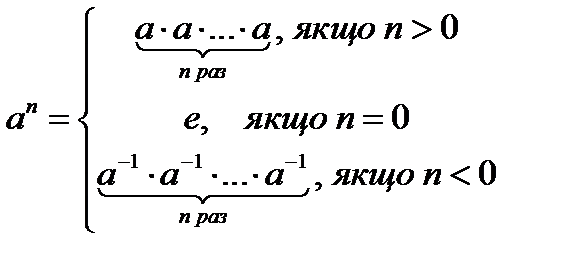

 а
а  G,
G,  m, n
m, n 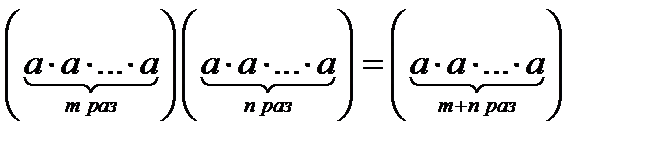 = am + n.
= am + n.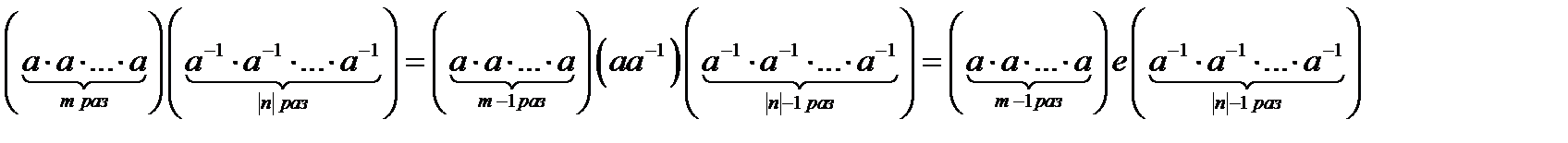 =
= 
 а
а  G) (
G) ( можна розповсюдити на довільну скінчену кількість співмножників
можна розповсюдити на довільну скінчену кількість співмножників :(
:( 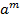 ) n =
) n = 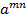
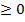 . Тоді на підставі властивості 4
. Тоді на підставі властивості 4  і означення 4
і означення 4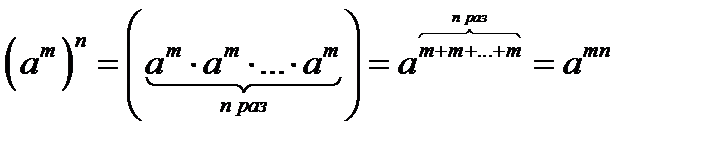
 =
= 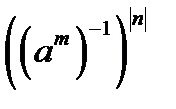 =
=  =
= 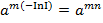 .
.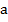 замінюється поняттям n-кратного елемента
замінюється поняттям n-кратного елемента 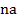 елементу
елементу 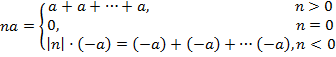
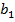 =а
=а 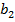 (
(  К) випливає:
К) випливає: 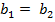 . Це означає, що рівності можна скорочувати на ненульовий елемент, який не є дільником нуля.
. Це означає, що рівності можна скорочувати на ненульовий елемент, який не є дільником нуля.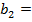 0
0 )=0.
)=0. справедлива рівність
справедлива рівність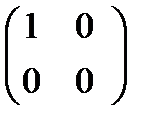
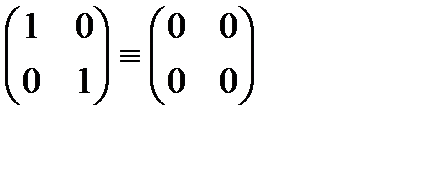
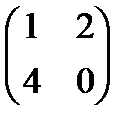
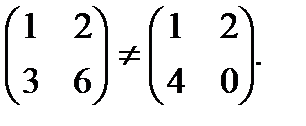
 кільця К, яка сама є кільцем відносно операцій, означених в К, називається підкільцем кільця К.
кільця К, яка сама є кільцем відносно операцій, означених в К, називається підкільцем кільця К. кільця К є підкільцем кільця К тоді і тільки тоді, коли
кільця К є підкільцем кільця К тоді і тільки тоді, коли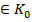 ): а+ b
): а+ b 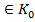 .
.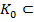 К є підкільцем К, то виконання умов 1)-3) гарантоване означенням кільця К.
К є підкільцем К, то виконання умов 1)-3) гарантоване означенням кільця К.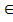 Р справедливо:
Р справедливо: усіх діагональних матриць n-го порядку є підкільцем кільця М
усіх діагональних матриць n-го порядку є підкільцем кільця М  усіх матриць n -го порядку над полем Р, бо сума, добуток діагональних матриць, і матриця, протилежна до діагональної, є діагональними.
усіх матриць n -го порядку над полем Р, бо сума, добуток діагональних матриць, і матриця, протилежна до діагональної, є діагональними.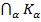 теж є підкільцем кільця К.
теж є підкільцем кільця К.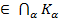 = Ко. Якщо а, b
= Ко. Якщо а, b 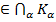 =
= 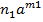 +
+ 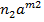 +….+
+….+ 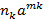 ,
,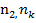 - довільні цілі числа,
- довільні цілі числа, 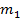 ,
, 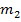 ,..
,.. 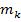 довільні натуральні числа, утворює підкільце кільця К, яке називається підкільцем, породженим елементом a. За означенням
довільні натуральні числа, утворює підкільце кільця К, яке називається підкільцем, породженим елементом a. За означенням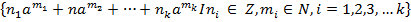
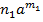 +
+  +….+
+….+ 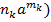 +(
+( 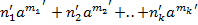 ) =(
) =( 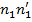 )
) 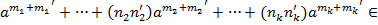 Кα
Кα 2.Гомоморфізми та ізоморфізми кілець
2.Гомоморфізми та ізоморфізми кілець що
що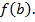
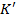 називається гомоморфізмом, якщо
називається гомоморфізмом, якщо
 =
=  .
. ) (
) ( 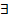 а
а 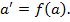
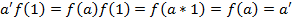
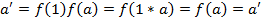
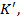 тобто f (1)=
тобто f (1)= 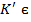 областю цілісності з одиницею
областю цілісності з одиницею 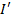 , то для всякого гомоморфізму f: K
, то для всякого гомоморфізму f: K 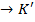 справедливо f (1) =
справедливо f (1) =  1)=f(a)f(1)
1)=f(a)f(1)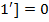
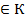 ): f (a)=0), то з наступної рівності виходить, що f (1)=
): f (a)=0), то з наступної рівності виходить, що f (1)=  Якщо існує обернений елемент для
Якщо існує обернений елемент для 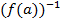 .
. )= f (1)=
)= f (1)=  }
}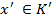 , для яких існують такі елементи х
, для яких існують такі елементи х 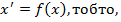
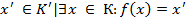 }.
}.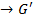 множини Ker f і Im f є підгрупами груп G і
множини Ker f і Im f є підгрупами груп G і 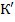 відповідно. До цього питання ми ще повернемось в параграфі 3.
відповідно. До цього питання ми ще повернемось в параграфі 3.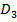 усіх діагональних матриць 3-го порядку.
усіх діагональних матриць 3-го порядку.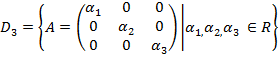
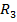 усіх трьохвимірних векторів
усіх трьохвимірних векторів
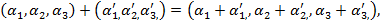
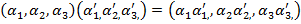

 таким способом: якщо
таким способом: якщо


