
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение нелинейных уравненийСодержание книги
Поиск на нашем сайте
Иррациональные числа, которые не могут быть корнем никакого алгебраического уравнения с целыми коэффициентами, называют трансцендентными числами. К таким числам относятся корни нелинейных уравнений, которые обычно решаются с помощью операторов IF – GOTO. Задача в общем виде формируется следующим образом. Пусть требуется с точностью Известно множество методов вычисления корня уравнения. Все они предлагают приближение к корню по формуле:
Функция Обычно значение
При вычислении этого неравенства искомое значение корня получается равным Количество циклов приближения неизвестно, поэтому требуется анализ с помощью IF. Студентам предлагается 3 метода решения нелинейных уравнений: метод простой итерации, метод Ньютона и метод деления пополам (метод бисекций).
Метод простой итерации
Задано: Введем обозначения:
Тогда алгоритм решения будет следующим. 1. Задается значение 2. Вычисляется 3. Проверяется условие 4. Если условие выполняется (“истина”), то
Метод Ньютона
Задано: Введем обозначения:
Так как вычисления искомого значения Итак, алгоритм решения. 1. Задаем значение 2. Вычисляется 3. Вычисляется 4. Определяется 5. Проверяется условие Если условие выполняется, то
Метод деления пополам
Задано: При использовании этого метода интервал
Для перемещения
т.е. корень существует, если произведение функций при значениях концов интервала является отрицательным. Алгоритм решения следующий. 1. 2. Вычисляется 3. Вычисляется 4. Анализ 5. Анализ интервала 6. Анализируется 7. Вычисления отправляются к п.1 (через GOTO). Задание 1. 1. Составить схему алгоритма для вычисления функций, приведенных в таблице 5.6. 2. Написать программу на языке BASIC. 3. Произвести расчеты на микроЭВМ. 4. Распечатать листинг программы. 5. Исходные данные, промежуточные и окончательные результаты вывести на экран монитора и на печатающее устройство.
Задание 2. 1. Составить схему алгоритма для вычисления функций, приведенных в таблице 5.7. 2. Выполнить пп. 2 – 5 задания 1.
Таблица 5.6. Список заданий
Таблица 5.7. Список заданий
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.225 (0.006 с.) |

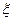 определить значение одного из корней нелинейного уравнения
определить значение одного из корней нелинейного уравнения 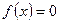 , исходя из значения начального приближения корня
, исходя из значения начального приближения корня 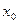 . При этом считается, что функция
. При этом считается, что функция 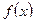 удовлетворяет условию, гарантирующим существование решения и сходимость последовательности приближений к точному значения корня.
удовлетворяет условию, гарантирующим существование решения и сходимость последовательности приближений к точному значения корня.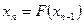 , где
, где 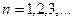
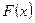 учитывает расчетную формулу метода и исходную функцию
учитывает расчетную формулу метода и исходную функцию 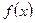 .
.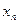 считают достаточно хорошим приближением к точному значению корня, если выполняется условие:
считают достаточно хорошим приближением к точному значению корня, если выполняется условие: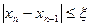
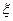 и
и 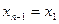 ,
, 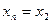 ,
, 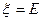 . При использовании метода простой итерации уравнение
. При использовании метода простой итерации уравнение 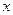 в общем виде:
в общем виде:
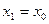 .
.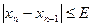
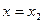 в противном случае
в противном случае 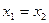 и следует повторять цикл с п.2 (через GOTO).
и следует повторять цикл с п.2 (через GOTO).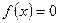 ,
, 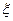 и
и 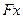 - левая часть нелинейного уравнения;
- левая часть нелинейного уравнения; 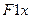 – первая производная от
– первая производная от 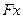 ;
;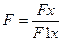 .
.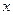 производится в этом методе иначе, чем в методе простой итерации, то значения
производится в этом методе иначе, чем в методе простой итерации, то значения 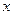 могут использоваться без индексов. Анализ нахождения искомого значения
могут использоваться без индексов. Анализ нахождения искомого значения 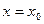
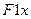 .
.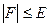
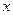 - искомый корень, в противном случае следует повторить цикл с п.2.
- искомый корень, в противном случае следует повторить цикл с п.2.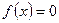 ,
, 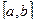 , где существует корень.
, где существует корень.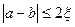 .
.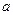 или
или 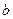 интервала
интервала 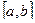 используется теорема Больцмана-Коши (о существовании корня внутри интервала):
используется теорема Больцмана-Коши (о существовании корня внутри интервала):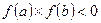 ,
,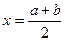 .
.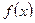 .
.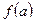 (или
(или 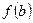 ).
).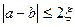 . Если условие выполняется, то выход из цикла; в противном случае надо сдвигать интервал по п.6.
. Если условие выполняется, то выход из цикла; в противном случае надо сдвигать интервал по п.6.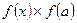 . Если
. Если 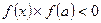 , то
, то 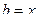 ; в противном случае
; в противном случае 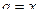 .
.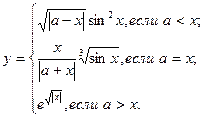
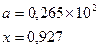
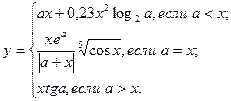
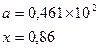
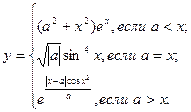
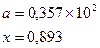
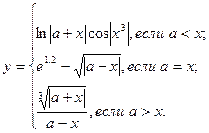
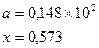
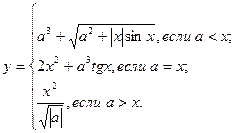
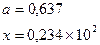
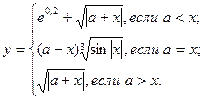
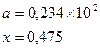
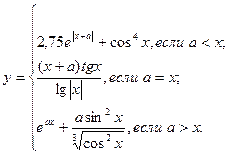
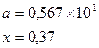
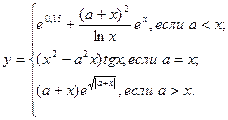
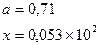
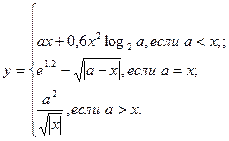
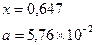
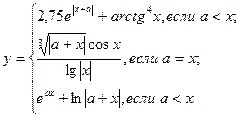
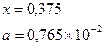
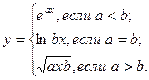 причем х – корень нелинейного уравнения ln x – x + 1,8 = 0, которое необходимо решить методом деления пополам с точностью e.
причем х – корень нелинейного уравнения ln x – x + 1,8 = 0, которое необходимо решить методом деления пополам с точностью e.
 причем х – корень нелинейного уравнения x – sin x = 0,25, которое необходимо решить любым методом с точностью e при начальном значении x0.
причем х – корень нелинейного уравнения x – sin x = 0,25, которое необходимо решить любым методом с точностью e при начальном значении x0.
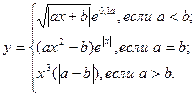 причем х – корень нелинейного уравнения x = e - x, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.
причем х – корень нелинейного уравнения x = e - x, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.
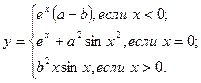 причем х – корень нелинейного уравнения x 2 – sin 5 x = 0, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.
причем х – корень нелинейного уравнения x 2 – sin 5 x = 0, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.
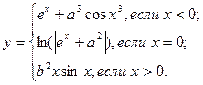 причем х – корень нелинейного уравнения x – sin x = 0,25, которое необходимо решить методом простой итерации с точностью e при начальном значении x0.
причем х – корень нелинейного уравнения x – sin x = 0,25, которое необходимо решить методом простой итерации с точностью e при начальном значении x0.
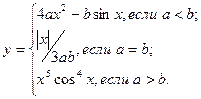 причем х – корень нелинейного уравнения x = e - x, которое необходимо решить методом деления пополам с точностью e.
причем х – корень нелинейного уравнения x = e - x, которое необходимо решить методом деления пополам с точностью e.
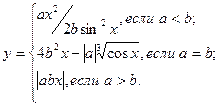 причем х – корень нелинейного уравнения x – sin 2 x = 0,25, которое необходимо решить методом простой итерации с точностью e при начальном значении x0.
причем х – корень нелинейного уравнения x – sin 2 x = 0,25, которое необходимо решить методом простой итерации с точностью e при начальном значении x0.
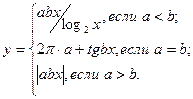 причем х – корень нелинейного уравнения x 2 – sin 5 x = 0, которое необходимо решить методом деления пополам с точностью e.
причем х – корень нелинейного уравнения x 2 – sin 5 x = 0, которое необходимо решить методом деления пополам с точностью e.
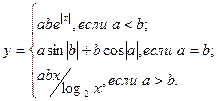 причем х – корень нелинейного уравнения x 3 – cos 2 x = 0, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.
причем х – корень нелинейного уравнения x 3 – cos 2 x = 0, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.
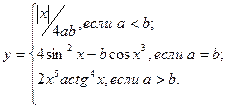 причем х – корень нелинейного уравнения 10 x = lnx + ex, которое необходимо решить методом деления пополам с точностью e.
причем х – корень нелинейного уравнения 10 x = lnx + ex, которое необходимо решить методом деления пополам с точностью e.



