
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тогда, коэффициент приведения длины будет равенСодержание книги
Поиск на нашем сайте
и зависит от угла сдвига γ1, величина которого различна для разных систем решеток. в) Колонны с безраскосной решеткой Эти колонны представляют собой рамную систему, все элементы которой при общем изгибе колонны изгибаются по S-образным кривым (рисунок 9.6). Приближенно принимаем, что нулевые точки моментов расположены в середине планок по длине и посередине расстояния между планками в ветвях колонны. В нулевых точках действуют поперечные силы Q от изгиба стержня и поровну распределены между ветвями. Тогда γ1 =
Рисунок 9.6 - Деформации стержней с планками при продольном изгибе Принимая J1=Ab×i12; Jy=2·Ab×iy2; lb/i1 = l1 (гибкость ветви), l/iy= ly (гибкость стержня), i1- радиус инерции одной ветви, получим
Отсюда приведенная гибкость стержня с планками в 2-х плоскостях λef = μ·λy = с планками в 4-х плоскостях определяется по условной гибкости
Приведенная гибкость стержней треугольного сечения
где λ - наибольшая гибкость всего сечения; λ1; λ2 и λ3 - гибкость ветвей относительно собственных осей, параллельных главным осям, определяются на участках между планками (в осях) и принимаются не более 40. г) Колонны с треугольной решеткой и дополнительными распорками
Для этих колонн угол перекоса (рисунок 9.7) определяется по формуле γ1 = При наличии двух решеток и при Q = 1 усилие в раскосе будет равно Nd = а удлинение раскоса определится по формуле Δd = где Ad - площадь сечения раскоса, тогда
Приведенная гибкость с 2-мя решетками в 2-х плоскостях λef =μ·λy = и с 4-мя решетками λef = Для стержней трехгранного сечения с равными сторонами λef = Коэффициенты α1 и α2 зависят от угла наклона раскоса α = В составных стержнях с решетками гибкость отдельных стержней между узлами должна быть не более 80 и не превышать λef. Кроме устойчивости всего стержня необходима проверка устойчивости отдельной ветви между узлами. д) Поперечная сила при продольном изгибе Возникает в результате изгиба стержня при потере устойчивости и воспринимается решетками. Q = где ƒcr – прогиб при потере устойчивости. СНиП предлагает формулу определения условной Q в зависимости от Rу, ƒ и А Qfic=7.15×10-6·(2330 - где φ – коэффициент устойчивости при центральном сжатии. Достаточно близкие значения Qfic можно принять по таблице 9.1. Таблица 9.1 А в см2
Для других сталей значение А следует интерполировать.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.246.110 (0.007 с.) |

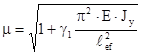 (9.6)
(9.6)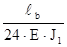 и подставив в (9.6) (9.7) получим
и подставив в (9.6) (9.7) получим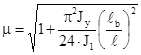 . (9.8)
. (9.8)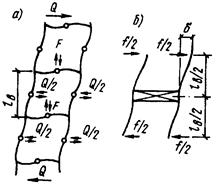
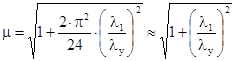 . (9.9)
. (9.9)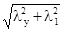 , (9.10)
, (9.10) . (9.11)
. (9.11)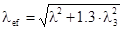 , (9.12)
, (9.12)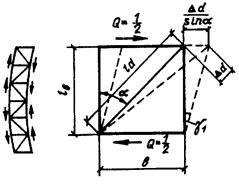
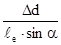 . (9.13)
. (9.13)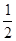 sinα, (9.14)
sinα, (9.14)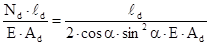 , (9.15)
, (9.15)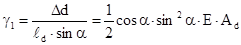 , (9.16)
, (9.16)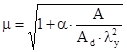 . (9.17)
. (9.17)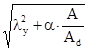 (9.18)
(9.18)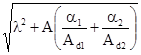 . (9.19)
. (9.19)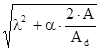 . (9.20)
. (9.20)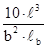 . (9.21)
. (9.21)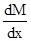 = Ncr·
= Ncr· 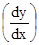 =
= 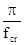 ·A·scr, (9.22)
·A·scr, (9.22)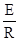 )×
)× 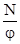 , (9.23)
, (9.23)


