
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотез о равенстве средних
Гипотеза о равенстве двух средних значений произвольно распределённых генеральных совокупностей (большие независимые выборки). При уровне значимости a нужно проверить гипотезу Н 0:
имеющую нормальное распределение, причём M (Z) = 0, D (Z) = 1. Определяется соответствующее экспериментальное значение z экс. Из таблицы функции Лапласа находится критическое значение z кр. При альтернативной гипотезе Н 1: Гипотеза о равенстве двух средних значений нормально распределённых генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки). При уровне значимости a нужно проверить основную гипотезу Н 0:
имеющую распределение Стьюдента с (n х + n у – 2) степенями свободы. Определяется соответствующее экспериментальное значение t экс. Из таблицы критических точек распределения Стьюдента (Приложение 4) находится критическое значение t кр. Гипотеза о равенстве двух дисперсий нормально распределённых генеральных совокупностей. В данном случае при уровне значимости a нужно проверить гипотезу Н 0: D (Х) = D (Y). Статистикой служит случайная величина
имеющая распределение Фишера – Снедекора с f 1 = n б – 1 и f 2 = n м – 1 степенями свободы ( Задания 13 1- 14 0 Заданы две выборки. 1) Для обеих выборок вычислите среднее, исправленную дисперсию и среднее квадратическое отклонение. Найдите размах варьирования, среднее абсолютное (линейное) отклонение, коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции.
2) Предполагая, что данная случайная величина имеет нормальное распределение, определите доверительный интервал для генеральной средней (в обоих случаях). 3) По критерию Фишера проверьте гипотезу о равенстве генеральных дисперсий. 4) По критерию Стьюдента проверьте гипотезу о равенстве генеральных средних (альтернативная гипотеза – об их неравенстве). Во всех расчётах уровень значимости a = 0,05.
131. Выборка 1: 36; 19; 22; 39; 20; 26; 21; 26; 26, Выборка 2: 28; 24; 26; 26; 48; 22; 33 (в ньютонах). 132. Выборка 1: 128; 192; 223; 398; 205; 266; 219; 260; 264; 98. Выборка 2: 286; 240; 263; 266; 484; 223; 335. (условных единиц). 133. Выборка 1: 52, 48, 46, 55, 62, 58, 64 и 56 мин. Выборка 2: 51, 47, 44, 52, 56 и 48 мин. 134. Выборка 1: 25, 30, 42, 48, 52, 55 и 66 (условных единиц). Выборка 2: – 28; 28; 38; 38; 45; 56; 59; 60; 64; 78. 135. Выборка 1: 360; 319; 322; 339; 350; 326; 361; 326; 386. Выборка 2: 368; 354; 326; 346; 348; 357; 383 (секунд). 136. Выборка 1: 25, 130, 242, 48, 152, 138, 55 и 136 секунд. Выборка 2: 28; 128; 138; 235; 45 и 156 секунд. 137. Выборка 1: 40, 78, 89, 122, 146 и 198 кг. Выборка 2: 38, 69, 77, 99, 126, 142, 158, 162 и 226 кг. 138. Выборка 1: 8, 12, 16, 18, 24 и 44 г. Выборка 2: 8, 9, 14, 17, 19, 26, 26, 33 и 54 г. 139. Выборка 1: 50,4; 53,6; 54,4; 46,4; 44,0; 48,2; 49,4. Выборка 2: 47,2; 62,4; 64,8; 62,4; 58,9; 55,4; 66,2; 49,5; 67,8; 68,9 (ньютонов). 140. Выборка 1: 0,42, 0,52, 0,48, 0,46, 0,55, 0,62, 0,58, 0,64 и 0,56 секунд. Выборка 2: 0,51, 0,67, 0,54, 0,52, 0,56, 0,66 и 0,68 секунд. Пример выполнения заданий 13 1- 14 0 Из первого нарезного оружия было произведено 8 выстрелов. При этом измерялись начальные скорости пуль. Получены следующие результаты: 902,4; 901,3; 898,4; 903,5; 901,1; 900,4; 899,7 и 900,3 (м/с). Из второго оружия было произведено 7 выстрелов. Скорости вылета пуль оказались равны 905,5; 910,3; 903,8; 902,4; 899,9; 903,3 и 905,6 (м/с). Для обеих выборок вычислите среднее, исправленную дисперсию и среднее квадратическое отклонение. Найдите размах варьирования, среднее абсолютное (линейное) отклонение, коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции. Предполагая, что данная случайная величина имеет нормальное распределение, определите доверительный интервал для генеральной средней (в обоих случаях).
По критерию Фишера проверьте гипотезу о равенстве генеральных дисперсий. По критерию Стьюдента проверьте гипотезу о равенстве генеральных средних (альтернативная гипотеза – об их неравенстве). Во всех расчётах уровень значимости a = 0,05. Решение. Для первого оружия вычислим среднее значение, исправленную дисперсию и исправленное среднее квадратическое отклонение:
Для первого оружия находим другие характеристики вариации: - размах варьирования R = xmax – xmin = 903,5 – 898,4 = 5,1; - среднее абсолютное (линейное) отклонение
- коэффициент вариации -линейный коэффициент вариации - коэффициент осцилляции Для доверительной вероятности g = 0,95 (уровень значимости a = 0,05) по таблице критических точек распределения Стьюдента при f = 8 – 1 = 7 степенях свободы находим значение коэффициента t g = 2,36. Тогда полуширина доверительного интервала
И с вероятностью g = 0,95 генеральное среднее начальной скорости пули лежит в интервале (900,76 ± 1,24) м/с или (899,52; 902,00) м/с. Повторим все расчёты для второго оружия:
R = ymax – ymin = 905,5 – 899,9 = 5,6;
Для доверительной вероятности g = 0,95 (уровень значимости a = 0,05) по таблице критических точек распределения Стьюдента при f = 7 – 1 = 6 степенях свободы находим значение коэффициента t g = 2,45. Тогда полуширина доверительного интервала
И с вероятностью g = 0,95 генеральное среднее начальной скорости пули лежит в интервале (902,69 ± 1,63) м/с или (901,03; 904,32) м/с. Проводим проверку гипотезы о равенстве дисперсий: H 0: Dx = Dy; H 1: Dx < Dy. Найдём наблюдаемое значение критерия Фишера
f 1 = n б – 1 = n у – 1 = 7 – 1 = 6 и f 2 = n м – 1 = n х – 1 = 8 – 1 = 7 (числа степеней свободы). По таблице критических точек распределения Фишера – Снедекора (Приложение 5) при уровне значимости a = 0,05 и данным числам степеней свободы находим F кр = 3,87. Т.к. F экс < F кр, то нет оснований отвергать нулевую гипотезу (т.е. можно считать, что дисперсии двух выборок равны). Проводим проверку гипотезы о равенстве генеральных средних: H 0: H 1: Найдём экспериментальное значение критерия Стьюдента
Число степеней свободы f = n х + n у – 2 = 8 + 7 – 2 = 13. По таблице критических точек распределения Стьюдента (Приложение 4) при уровне значимости Элементы теории корреляции Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Две случайные величины могут быть связаны либо функциональной зависимостью, либо статистической, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены влиянию случайных факторов, причем среди них могут быть и общие для обеих величин. В этом случае возникает статистическая зависимость. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, при изменении одной величины изменяется среднее значение другой. В таком случае статистическую зависимость называют корреляционной.
Приведем пример случайной величины Уравнением регрессии Уравнением регрессии х на Условное математическое ожидание
Это уравнение называют выборочным уравнением регрессии Как же найти по данным наблюдений параметры функции
|
|||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.13.201 (0.026 с.) |
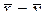 . Если объём обеих выборок велик, то можно считать, что выборочные средние имеют нормальное распределение, а их дисперсии известны. В этом случае в качестве статистики можно использовать случайную величину
. Если объём обеих выборок велик, то можно считать, что выборочные средние имеют нормальное распределение, а их дисперсии известны. В этом случае в качестве статистики можно использовать случайную величину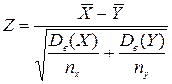 ,
,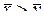 оно находится из условия F (z кр) = 0,5 – a. Если z экс < z кр, то нулевая гипотеза принимается, в противоположном случае – отвергается. При альтернативной гипотезе Н 1:
оно находится из условия F (z кр) = 0,5 – a. Если z экс < z кр, то нулевая гипотеза принимается, в противоположном случае – отвергается. При альтернативной гипотезе Н 1:  критическое значение находится из условия F (z кр) = 0,5×(1 – a). Нулевая гипотеза принимается, если | z экс | < z кр.
критическое значение находится из условия F (z кр) = 0,5×(1 – a). Нулевая гипотеза принимается, если | z экс | < z кр. ,
,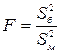 ,
,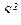 – большая дисперсия, объём её выборки n б). Определяется соответствующее экспериментальное (наблюдаемое) значение F экс. Критическое значение F кр при альтернативной гипотезе Н 1: D (Х) > D (Y) находится из таблицы критических точек распределения Фишера – Снедекора (Приложение 5) по уровню значимости a и числу степеней свободы f 1 и f 2. Нулевая гипотеза принимается, если F экс < F кр.
– большая дисперсия, объём её выборки n б). Определяется соответствующее экспериментальное (наблюдаемое) значение F экс. Критическое значение F кр при альтернативной гипотезе Н 1: D (Х) > D (Y) находится из таблицы критических точек распределения Фишера – Снедекора (Приложение 5) по уровню значимости a и числу степеней свободы f 1 и f 2. Нулевая гипотеза принимается, если F экс < F кр.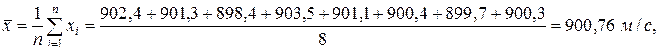

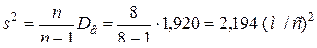 ,
,  .
.
 ;
;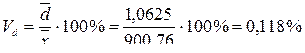 ;
;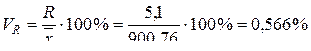 .
.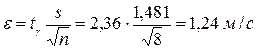 .
.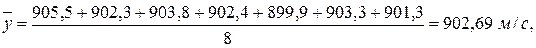
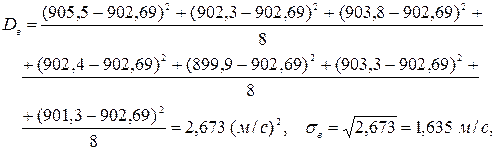
 ,
, 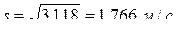 .
.
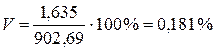 ;
; 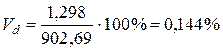 ;
;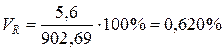 .
. .
. .
. ;
; .
.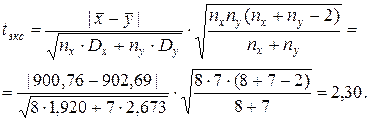
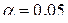 и данному числу степеней свободы находим t кр = 2,16. Т.к. t экс > t кр, то нулевая гипотеза отвергается, генеральные средние двух выборок не равны.
и данному числу степеней свободы находим t кр = 2,16. Т.к. t экс > t кр, то нулевая гипотеза отвергается, генеральные средние двух выборок не равны. от одной или нескольких других величин. Мы рассмотрим зависимость
от одной или нескольких других величин. Мы рассмотрим зависимость 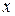 ). Рассмотрение зависимости
). Рассмотрение зависимости  .
.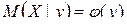 .
.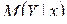 является функцией от х, следовательно, его оценка, т.е. условное среднее
является функцией от х, следовательно, его оценка, т.е. условное среднее 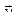 , также является функцией от х. Обозначив эту функцию
, также является функцией от х. Обозначив эту функцию  , получим уравнение:
, получим уравнение: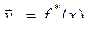 .
.


