
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения метода конечных элементов в перемещениях
Для применения МКЭ выполняют следующую последовательность процедур: 1) Разбивают тело на простые конечные элементы (КЭ). Вместе все КЭ полностью покрывают весь объем тела. Каждый КЭ имеет несколько опорных точек (узлов). 2) Если узел лежит на границе двух КЭ, то он является общим для них (узлы скрепляют КЭ между собой, обеспечивая совместность перемещений на границах). 3) Перемещения внутренних точек КЭ однозначно выражают через перемещения его узлов с помощью интерполяционных формул (функций формы КЭ). Это обеспечивает совместность перемещений внутри элемента. 4) Деформации выражают через перемещения. Это обеспечивает совместность деформаций. 5) Напряжения вычисляют по деформациям на основе закона Гука и закона течения. 6) Получают систему уравнений относительно неизвестных перемещений узлов. Каждое уравнение является уравнением равновесия одного узла под действием на него внешних сил и сил со стороны присоединенных к нему элементов. 7) Решают систему уравнений, находят перемещения узлов, по ним находят деформации в любой точке любого элемента, а по деформациям находят напряжения. КЭ обеспечивают кусочную аппроксимацию полей деформаций и напряжений всего тела (в каждом КЭ своя аппроксимирующая функция, они стыкуются между собой на границах элементов). В основе метода лежит интегральное вариационное уравнение (12.92), поэтому в ходе реализации метода приходится вычислять интегралы сложных функций по объему и поверхности сложного тела. МКЭ упрощает эти процедуры:
Вначале весь объем интегрирования разбивают на сумму объемов КЭ. Затем подынтгральную функцию 1) сложную геометрическую форму тела разбивают на небольшие элементы с простой геометрией; 2) сложную функцию Метод конечных элементов разрабатывали вначале для расчета стержневых конструкций. Каждый элемент представлял собой стержень с двумя узлами на концах. Для сплошного плоского тела простейший КЭ – треугольник с тремя узлами. На такие КЭ всегда можно разбить любое плоское тело.
Аппроксимируя перемещения внутренней точки
получим формулу, применимую для всех точек КЭ, в том числе и для трех его узлов. Это позволяет составить систему из шести уравнений и выразить шесть неизвестных коэффициентов формулы (12.93) через координаты После всех преобразований получим линейную связь
где 1) Если задать 2) Если точка Для нахождения функций формы в треугольном КЭ можно соединить точку
а функции формы равны следующим отношениям:
Рис. 12.28. Треугольный КЭ
Выражения (12.94) можно записать в тензорной форме и применять для любых конечных элементов:
где
(каждая функция формы в одном из узлов, при Функция
где матрицу градиентов элемента Подставим выражения
является условием равновесия одного узла (m) по одной оси (k). В этом уравнении Для всех узлов получаем систему уравнений (12.99). Число этих уравнений равно числу неизвестных Наиболее эффективный способ решения таких систем уравнений – итерационный, с решением на каждой итерации системы линейных алгебраических уравнений. Для получения такой системы из уравнений (12.99) необходимо представить выражение связи компонент напряжения
Здесь
либо упруго-пластическая матрица материала
Упруго-пластическая матрица материала (12.102), в отличие от упругой (12.101), учитывает изменение жесткости материала по различным направлениям в процессе пластической деформации. Выражение (12.100) означает, что каждый компонент напряжения зависит от всех компонент приращения деформации. Применение более сложных нелинейных зависимостей приводит к резкому замедлению решения. Запись в выражении (12.100) Чтобы получить систему уравнений относительно неизвестных перемещений узлов, подставим в (12.100) вместо
а затем полученное выражение для
Это линейная система уравнений:
где
Если все узлы находятся в равновесии, то Процедура расчета НДС сводится к составлению системы уравнений (12.106) и решению ее методом Гаусса. Граничные условия в перемещениях позволяют непосредственно определить часть перемещений в узлах, лежащих на поверхности. Перемещения в остальных узлах определяют из системы уравнений. Результатом решения являются приращения перемещений в узлах
|
|||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.151.158 (0.022 с.) |
 .
. аппроксимируют так, что в пределах каждого КЭ
аппроксимируют так, что в пределах каждого КЭ  . Упрощения достигают за счет того, что:
. Упрощения достигают за счет того, что: по двум осям линейными функциями
по двум осям линейными функциями , (12.93)
, (12.93) и компоненты перемещений
и компоненты перемещений  узлов
узлов  конечного элемента (рис. 12.28).
конечного элемента (рис. 12.28). с
с 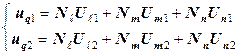 , (12.94)
, (12.94)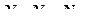 – функции от координат узлов
– функции от координат узлов  (функции формы КЭ). Эти функции линейные, как и исходные выражения (12.93). Их свойства:
(функции формы КЭ). Эти функции линейные, как и исходные выражения (12.93). Их свойства: , то и
, то и 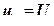 , следовательно,
, следовательно,  для любой точки
для любой точки  ), то
), то 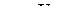 , следовательно, в каждом узле значение одной из функций равно 1, значение остальных двух равно 0.
, следовательно, в каждом узле значение одной из функций равно 1, значение остальных двух равно 0.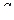 с узлами
с узлами  . Общая площадь КЭ равна сумме этих площадей
. Общая площадь КЭ равна сумме этих площадей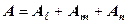 ,
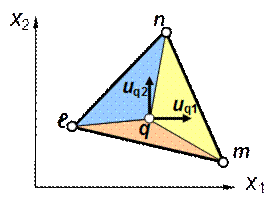
, .
.
 , (12.95)
, (12.95)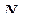 - вектор функций формы элемента, зависящих от координат точки и геометрии элемента; m - номер узла в элементе. Поскольку узлы также принадлежат элементу, то в каждом узле j
- вектор функций формы элемента, зависящих от координат точки и геометрии элемента; m - номер узла в элементе. Поскольку узлы также принадлежат элементу, то в каждом узле j (12.96)
(12.96) , обращается в единицу, а во всех остальных узлах - в нуль). Внутри элемента функции
, обращается в единицу, а во всех остальных узлах - в нуль). Внутри элемента функции 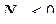 и
и  , но их сумма для любой точки равна единице.
, но их сумма для любой точки равна единице.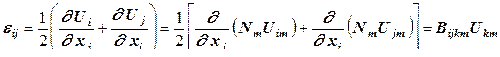 , (12.97)
, (12.97) получают дифференцированием вектора
получают дифференцированием вектора  . Таким образом, компоненты деформации во внутренних точках линейно зависят от перемещений узлов.
. Таким образом, компоненты деформации во внутренних точках линейно зависят от перемещений узлов. и
и  из (12.95) и (12.97) в интегральное уравнение (12.92):
из (12.95) и (12.97) в интегральное уравнение (12.92): .
.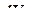 можно вынести из подынтегральных выражений, поскольку перемещения узлов не являются функциями от координат точек КЭ:
можно вынести из подынтегральных выражений, поскольку перемещения узлов не являются функциями от координат точек КЭ: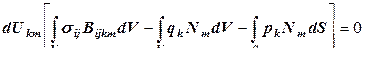 . (12.98)
. (12.98)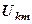 , поэтому совместность деформаций обеспечена при любых
, поэтому совместность деформаций обеспечена при любых 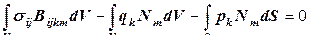 (12.99)
(12.99)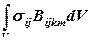 – равнодействующая напряжений по оси k в КЭ, окружающих узел m;
– равнодействующая напряжений по оси k в КЭ, окружающих узел m;  и
и 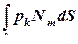 – равнодействующие нагрузок
– равнодействующие нагрузок  и
и  , распределенных по объему КЭ, окружающих узел m, и по поверхности их границ.
, распределенных по объему КЭ, окружающих узел m, и по поверхности их границ.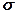 с компонентами приращения деформации за шаг решения
с компонентами приращения деформации за шаг решения  в линейном виде:
в линейном виде: . (12.100)
. (12.100) - упругая матрица материала
- упругая матрица материала , (12.101)
, (12.101) , (12.102)
, (12.102) - тензор начальных напряжений (значение
- тензор начальных напряжений (значение  при
при  ),
), . (12.103)
. (12.103) - в приращениях наиболее удобна с точки зрения организации вычислений. Весь процесс нагружения разбивают на шаги, и итоговые деформации и перемещения определяют как сумму перемещений на отдельных шагах. Использование напряжений
- в приращениях наиболее удобна с точки зрения организации вычислений. Весь процесс нагружения разбивают на шаги, и итоговые деформации и перемещения определяют как сумму перемещений на отдельных шагах. Использование напряжений  позволяет обеспечивать равновесие напряжений в конце каждого шага и автоматически корректировать погрешности в равновесии тела, возникающие вследствие ограниченной точности расчета.
позволяет обеспечивать равновесие напряжений в конце каждого шага и автоматически корректировать погрешности в равновесии тела, возникающие вследствие ограниченной точности расчета.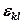 выражение из (12.97):
выражение из (12.97):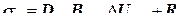 , (12.104)
, (12.104)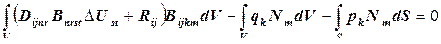 .
.  . (12.105)
. (12.105)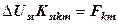 , (12.106)
, (12.106) - матрица жесткости тела,
- матрица жесткости тела,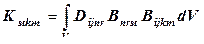 - (12.107)
- (12.107) - вектор объемных и поверхностных внешних нагрузок, включающих в себя и составляющие от неуравновешенных начальных напряжений,
- вектор объемных и поверхностных внешних нагрузок, включающих в себя и составляющие от неуравновешенных начальных напряжений, . (12.108)
. (12.108) и
и  (перемещений нет). Если равновесие нарушено, возникают перемещения узлов
(перемещений нет). Если равновесие нарушено, возникают перемещения узлов  , приводящие конечно-элементную модель в равновесное состояние.
, приводящие конечно-элементную модель в равновесное состояние.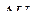 , по которым могут быть найдены любые компоненты НДС.
, по которым могут быть найдены любые компоненты НДС.


