Тема 1.1 Математические понятия.

 

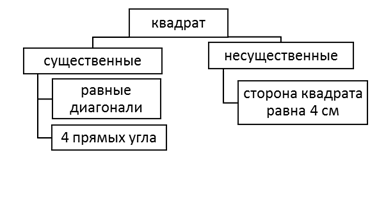
Математика, как и другие науки, изучает окружающий нас мир, природные и общественные явления, но изучает лишь их особые формы. Например, в геометрии изучают формы и размер не принимая другие их свойства: цвет, массу твердость и т.д. От всего этого отвлекаются, абстрагируются.

Следовательно, математика изучает абстрактные понятия и свойства абстрактных понятий.

Возникает вопрос: как же сложилось такое представление о математических объектах и зачем оно нужно?

Первая причина состоит в том, что практика и наглядное представление всегда показывали и показывают возможность сделать формы тел и геометрическое построение более точными.

Вторая причина, сложилась как следствие первой, точное рассуждение требует идеально точно определенного предмета.

В своем развитии математика прошла несколько этапов, создавая на каждом из них определенные способы познания и осмысления разнообразных форм количественных отношений материального мира.

Метод изучения действительности – метод построения математических моделей.

Абстрактность математики позволяет применять ее в самых разных областях знания, поскольку она представляет собой могущественные инструмент познания природы и создания техники.

Объем и содержание понятия.

Всякий математический объект обладает определенными свойствами. Среди свойств объекта различают свойства существенные и несущественные для его выделения из других объектов.

Существенные свойства объекта – свойства присущие данному объекту, без которых он не может существовать.

Несущественные свойства объекта – такие свойства, отсутствие которых не влияет на существование объекта.

Понятие об объекте складывается, главным образом, из знаний его существенных свойств.

Содержанием понятия называют совокупность всех взаимного существенных свойств объекта.

Объем понятия – это совокупность всех объектов, обозначаемых одним и тем же термином.

Например, объем понятия «прямоугольные треугольники» «меньше» чем объем понятия «треугольники».

Дошкольный курс насыщен различными математическими понятиями, которые в большинстве своем можно так или иначе встретить в реальной жизни. Тем самым изучение математики опирается на его историю развития.

Определение понятий

В содержании какого-либо математического объекта существует много существенных свойств. Однако, чтобы установить находиться ли объект в объеме понятия, необходимо проверить наличие только некоторых существенных свойств. Указание существенных свойств объекта, которых достаточно для распознания объекта, называются определение понятия.

Определение понятия – логическая операция, раскрывающая содержание понятия.

Существует явные и неявные определения.

Явные определения имеют определяющее понятие, через которое раскрывается смысл определяемого понятия с помощью видового отличия.

Например, квадрат = прямоугольник + все равные стороны.

В явных определениях можно выделить два подвида, которые чаще всего встречаются в курсе математики, такие как, генетические и рекурсивные определения.

Генетическим определением будем называть определение, где частным случаем будем указывать определения через род и видовое отличие, когда видовое отличие будет указывать на происхождение или способ построения определяемого определения.

Например, Угол – это фигура, которая состоит из точек вершины угла и двух лучей, выходящих из этой точки, - сторон угла.

Рекурсивные определения – определения, в которых указывается некоторые основные элементы из объема понятия, а также даются правила, которые позволяют получать из уже имеющихся элементов – новые.

Например, Арифметической прогрессией называется числовая последовательность, каждый член которой, начинается со второго, равен предыдущему, сложенному с одним и тем же числом.

Под неявными принято понимать определение понятия с помощью наглядности конкретных объектов, охватываемых этим понятием.

Остенсивными (от лат. ostendere – показывать) определениями принято пользоваться для введения терминов путем показа объектов, которые этими терминами обозначают.

Например, «Прочитай записи:

9 + 71 30 + 6 + 14 18 – (14 + 6)

23 – 37 15 – 7 + 32  25 – (15 – 10)

Это числовые выражения, или, короче, выражения».

В контекстуальных определениях содержание нового понятия вводится через контекст, отрывок текста, анализ конкретной ситуации, раскрывающей смысл вводимого понятия.

Например, Понятие «натуральное число» в математике в учебнике Дорофеева Г.В., Миракова Т.Н., Бука Т.Б. за 1 класс вводиться следующим образом: «Все предметы вокруг можно считать, используя слова один, два, три, четыре, пять, …»

Требования к определению понятий

1. Определение должно быть соразмерным.

2. В определении (или их системе) не должно быть порочного круга.

3. Определение должно быть ясным.

Таким образом, чтобы определение было ясным, желательно, чтобы оно не содержало избыточных свойств в определяющей части, т.е. таких свойств, которые могут быть выведены из других, включенных в это определение. Однако иногда для простоты изложения это правило нарушают.

Например, избыточное определение: «Прямоугольником называется четырехугольник, у которого противоположные стороны равны и все углы прямые».

Лучше сказать: «Прямоугольником называют четырёхугольник, у которого все углы прямые».

 

Практические задания

 

Ответьте на вопросы:

1) Что такое содержание понятия?

2) Что такое объем понятия?

3) Какие существуют свойства понятия объекта?

4) Что такое определение понятия?

5) Какие виды определений выделяют?

6) Какие выделяются требования к определению понятия?

 

Задание 1: Заполните таблицу определив вид определения понятий. 

№	Определение понятия	Вид определения
1
2
3
4
5

 

Задание 2: Начертите три геометрические фигуры, принадлежащие объему понятия:

а) параллелограмм;

б) трапеция;

в) окружность.

 

Задание 3: Назовите пять существенных свойств понятия:

а) треугольник;

б) круг.

 

Задание 4: Находятся ли в отношении рода и вида следующие пары понятий:

а) многоугольник и треугольник;

б) угол и острый угол;

в) луч и прямая;

г) ромб и квадрат;

д) круг и окружность?

 

Задание 5: Изобразите при помощи кругов Эйлера отношения между объемами понятий а, в и с, если:

а) а – «четырехугольник», в – «трапеция», с – «прямоугольник»;  

б) а – «натуральное число, кратное 3», в – «натуральное число, кратное 4», с – «натуральное число»;

в) а – «треугольник», в – «равнобедренный треугольник», с – «равносторонний треугольник».

 

Задание 6: В следующих определениях выделите определяемое и определяющее понятие, родовое понятие (по отношению к определяемому) и видовое отличие:

а) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны;

б) Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией

 

Задание 7: Для каждого из данных понятий подберите родовое понятие и дополните определение.

а) Прямоугольник - это …, у которого противоположные углы прямые.

б) Прямоугольник - это….., у которого угол прямой.

в) Равнобедренный треугольник - это…у которого две стороны равны.

г) Квадрат - это…., у которого стороны равны.

 

Задание 8: Определите, какая ошибка допущена в определении (подчеркните ее номер):

1.    Не указано родовое понятие

2.    Родовое понятие указано неверно

3.    Не указано видовое отличие

4.    Видовое отличие указано неверно (или не полностью)

 

а)   Прямоугольник - это когда все углы прямые.

б)   Биссектриса угла - это луч, который исходит из его вершины.

в)   Квадрат - это четырехугольник, у которого все стороны равны.

г)    Медиана – это отрезок, который делит сторону пополам.

 

Задание 8: Дайте определение: тупоугольного треугольника, равнобедренного треугольника, трапеции. Какие понятия вы выбрали в качестве родового в каждом случае? Какие свойства включили в видовое отличие?