Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При нахождении первообразных, как и при нахождении производных, используются не только формулы, но и некоторые правила. ⇐ ПредыдущаяСтр 3 из 3
Правило 1. Первообразная суммы равна сумме первообразных. Правило 2. Постоянный множитель можно выносить за знак первообразной. Правило 3. Если функции
Зная формулы для вычисления производных, нетрудно составить таблицу для нахождения первообразных. Таблица первообразных
Пример 1. Проверить, что функция F(x) = х5+Зх2-cosx является первообразной функции f(x) = 5х4+6х+sinx. Решение: необходимо проверить выполнение формулы F'(x) = f(x).
Пример 2. Найти первообразную функции: a) f(x) = 3x2; б) f(x) = 8x7. Решение: Реши самостоятельно по образцу: №48.5, 48.6, 48.9, 48.10, 48.11
Пример 3. Найдите первообразную функции Решение: 1) Найдем общий вид всех первообразных для заданной функции 2) Решим уравнение
12-9+C=11 C=8 3) Найденное значение С=8 подставляем в выражение Это и будет ответ.
Неопределенный интеграл и его свойства Если функция Читается: «неопределенный интеграл эф от икс дэ икс». Функция Свойства неопределенного интеграла 1. 2. 3. 4. 5.
Таблица основных интегралов 1. 4. 7. 10. 13. Вычисление неопределенного интеграла Непосредственное интегрирование Метод непосредственного интегрирования связан с приведением подынтегрального выражения к табличной форме путем преобразований и применения свойств неопределенного интеграла.
Пример 4. Найдите неопределенный интеграл Решение: применяя свойство 4 и формулу 6, получаем Пример 5. Найдите неопределенный интеграл Решение: применяя свойство 4 и формулу 9, получаем
Пример 6. Найдите неопределенный интеграл Решение: Пример 7.
Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти одну ее первообразную и прибавить к ней произвольную постоянную С. Чтобы проверить, правильно ли найден неопределенный интеграл, необходимо продифференцировать (вычислить производную) полученную функцию; если при этом получается подынтегральное выражение, то интеграл найден верно. Реши самостоятельно по образцу: №997-1002.
Определенный интеграл Определенный интеграл - Читается: «интеграл от a до b эф от икс дэ икс».
Числа а и Пример 8. Пример 9. Для вычисления определенного интеграла 1) Первообразную F(x) для функции f(x) 2) Значение первообразной в точке x= a, т.е. F(a) 3) Значение первообразной в точке x= b, т.е. F(b) 4) Разность F(b)- F(a). Процесс вычисления виден из формулы определенного интеграла. Реши самостоятельно по образцу: №49.1, 49.2
Криволинейная трапеция
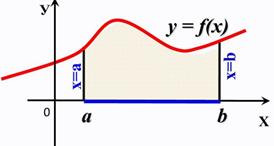
Пусть на отрезке [a, b] дана непрерывная неотрицательная функция y=f(x). Проведем вертикальные прямые х=а, х= b до пересечения с графиком функции f(x). Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке
Площадь криволинейной трапеции вычисляется по формуле Исходя из определения определенного интеграла следует, что площадь криволинейной трапеции вычисляется по формуле
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.122.195 (0.017 с.) |
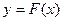 - первообразная для функции
- первообразная для функции 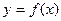 , то первообразной для
, то первообразной для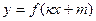 служит функция
служит функция 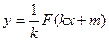 .
.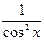
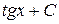
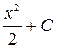
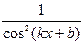
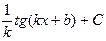
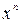
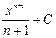
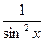
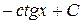
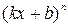
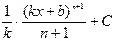
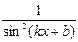
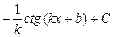
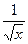
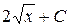
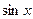
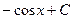
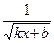
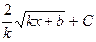
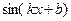
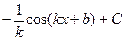
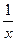
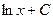
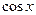
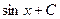
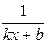
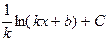
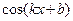
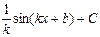
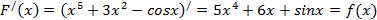
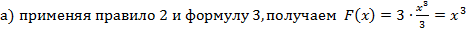
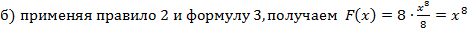
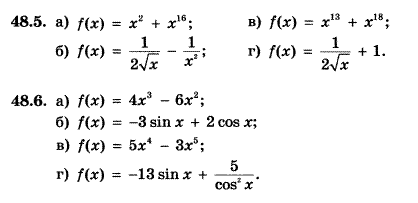
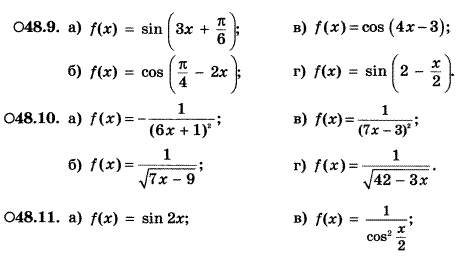
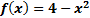 , график которой проходит через заданную точку
, график которой проходит через заданную точку 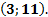
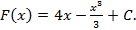
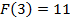 (3 и 11 – соответствующие координаты заданной точки).
(3 и 11 – соответствующие координаты заданной точки).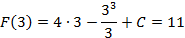
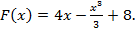
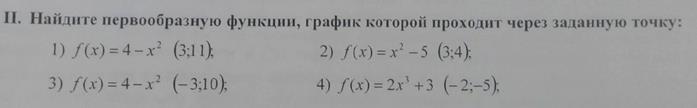 Реши самостоятельно по образцу: решить примеры под цифрой II
Реши самостоятельно по образцу: решить примеры под цифрой II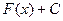 , где С – произвольная постоянная, называется неопределенным интегралом от функции
, где С – произвольная постоянная, называется неопределенным интегралом от функции 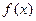 и обозначается символом
и обозначается символом 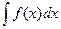 .
.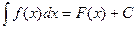 .
.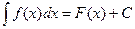
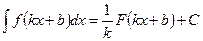
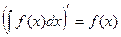
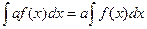 , где а – постоянная
, где а – постоянная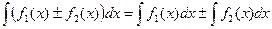
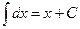 2.
2. 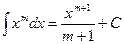 3.
3. 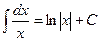
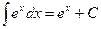 5.
5. 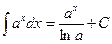 6.
6. 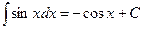
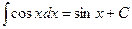 8.
8. 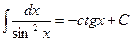 9.
9. 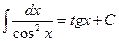
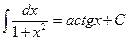 11.
11. 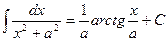 12.
12. 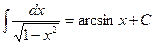
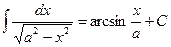 14.
14. 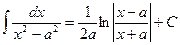
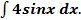
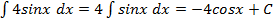
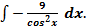
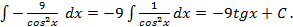
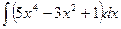
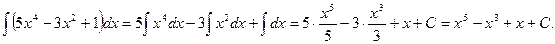
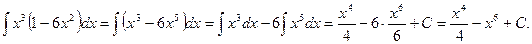
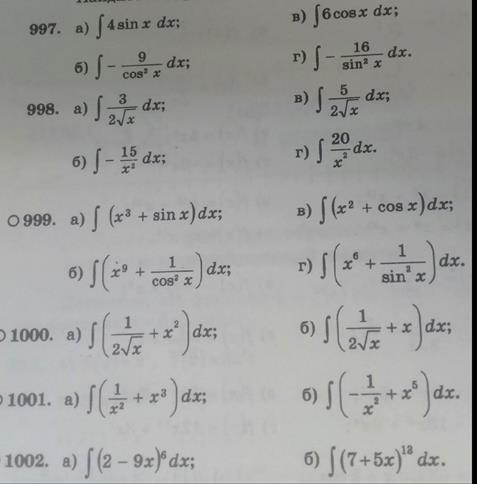
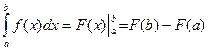 .
.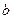 называются пределами интегрирования (а – нижний предел,
называются пределами интегрирования (а – нижний предел, 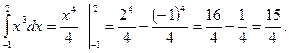
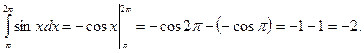
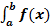 находят:
находят: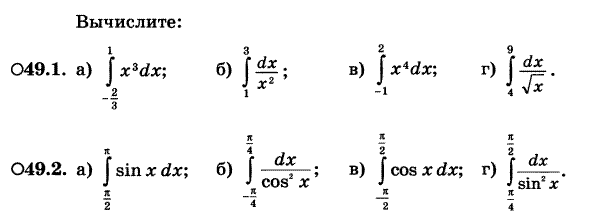
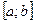 функции
функции 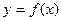 , осью ОХ и прямыми х = а и х =
, осью ОХ и прямыми х = а и х = 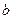 .
.
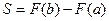 , где
, где 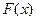 - первообразная для функции
- первообразная для функции