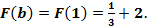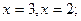Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8.2 Интегральное исчислениеСтр 1 из 3Следующая ⇒
Тема 8.2 Интегральное исчисление Первообразная функции Из школьного курса математики известно, что каждому математическому действию соответствует обратное ему действие. Так, вычитание есть действие, обратное сложению, деление — умножению и т. д. В предыдущей теме 8.1 рассмотрено новое действие — дифференцирование. Основной задачей дифференциального исчисления является нахождение производной или дифференциала заданной функции. Для дифференцирования существует обратное действие — интегрирование: нахождение функции по заданной ее производной или дифференциалу. Таким образом, если в процессе дифференцирования решается задача об отыскании скорости изменения функции, вызываемого изменением аргумента, то задачей интегрирования является нахождение самой функции по заданной скорости, ее изменения. Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной. Дифференцируемая функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство F'(x) = f(x). Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной. Примеры: 1) функция 2) функция Как всякое обратное действие, интегрирование вносит некоторое осложнение. Вспомним, как начинается изучение действий над числами. Сначала изучают только целые положительные числа. Наиболее простое действие — сложение — не вносит никаких затруднений. Однако стоит только перейти к обратному действию вычитанию, как встречается первое затруднение: вычесть из меньшего числа большее невозможно. Чтобы преодолеть эту трудность, в алгебре вводят отрицательные числа и вычитание становится возможным. При умножении целых чисел не встречается никаких затруднений; обратное же действие — деление — сразу вносит трудность. Оказывается, что далеко не все числа делятся друг на друга. Деление становится возможным с введением дробных чисел. Еще большие затруднения появляются при извлечении корня — действии, обратном возведению числа в целую положительную степень; здесь уже появляются затруднения в знаках. Так, корень четной степени из положительного числа имеет два знака, а корень четной степени из отрицательного числа не имеет действительного значения. Чтобы стало возможным извлечение корней целой положительной степени из действительных чисел, требуется ввести понятия об иррациональном числе, о мнимой единице, о мнимом числе и т. д. Интегрирование как действие, обратное дифференцированию, также вносит осложнение. Дифференцирование функции — однозначная операция, т. е. если функция имеет производную, то только одну. Обратная операция — отыскание первообразной — не однозначна. Так, функции F1(x) = x4, F2(x) = x4 + 5, F3(х) = x4+C, где С — любое постоянное действительное число, являются первообразными функции f(х) = 4х3, поскольку все эти функции имеют одну и ту же производную.
Если F(x) является первообразной функции f(х) на некотором промежутке, то множество всех первообразных этой функции имеет вид F(x)+С, где С — любое действительное число. Таким образом, любые две первообразные данной функции отличаются друг от друга на постоянное слагаемое, а выражение F(x)+C исчерпывает множество всех первообразных заданной функции f(x). Итак, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений. Геометрически выражение F(x)+C представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси Оу. Таблица первообразных
Пример 1. Проверить, что функция F(x) = х5+Зх2-cosx является первообразной функции f(x) = 5х4+6х+sinx. Решение: необходимо проверить выполнение формулы F'(x) = f(x).
Пример 2. Найти первообразную функции: a) f(x) = 3x2; б) f(x) = 8x7. Решение: Реши самостоятельно по образцу: №48.5, 48.6, 48.9, 48.10, 48.11
Пример 3. Найдите первообразную функции Решение: 1) Найдем общий вид всех первообразных для заданной функции
2) Решим уравнение
12-9+C=11 C=8 3) Найденное значение С=8 подставляем в выражение Это и будет ответ.
Таблица основных интегралов 1. 4. 7. 10. 13. Чтобы проверить, правильно ли найден неопределенный интеграл, необходимо продифференцировать (вычислить производную) полученную функцию; если при этом получается подынтегральное выражение, то интеграл найден верно. Реши самостоятельно по образцу: №997-1002.
Определенный интеграл Определенный интеграл - Читается: «интеграл от a до b эф от икс дэ икс».
Числа а и Пример 8. Пример 9. Для вычисления определенного интеграла 1) Первообразную F(x) для функции f(x) 2) Значение первообразной в точке x= a, т.е. F(a) 3) Значение первообразной в точке x= b, т.е. F(b) 4) Разность F(b)- F(a). Процесс вычисления виден из формулы определенного интеграла. Реши самостоятельно по образцу: №49.1, 49.2
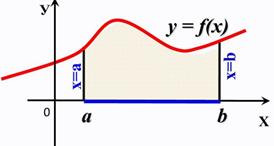
Криволинейная трапеция
Пусть на отрезке [a, b] дана непрерывная неотрицательная функция y=f(x). Проведем вертикальные прямые х=а, х= b до пересечения с графиком функции f(x). Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке
Площадь криволинейной трапеции вычисляется по формуле Исходя из определения определенного интеграла следует, что площадь криволинейной трапеции вычисляется по формуле Пример 10. Вычислить площадь криволинейной трапеции, ограниченной линиями Решение: 1) Построение криволинейной трапеции, ограниченной линиями:
2) Вычисляем первообразную для функции Получаем 3) Вычисляем 4) Вычисляем площадь по формуле Получаем
Реши самостоятельно №49.11 (а, в)
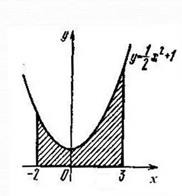
Пример 11. Вычислить площадь криволинейной трапеции, ограниченной линиями Решение: 1) Построение криволинейной трапеции, ограниченной линиями:
2) Вычисляем первообразную для функции Получаем 3) Вычисляем 4) Вычисляем площадь по формуле Получаем Реши самостоятельно: вычислить площадь криволинейной трапеции, ограниченной линиями: 1) 2) 3) 4) вычислить площадь криволинейной трапеции, изображенной на рисунке.
Тема 8.2 Интегральное исчисление Первообразная функции Из школьного курса математики известно, что каждому математическому действию соответствует обратное ему действие. Так, вычитание есть действие, обратное сложению, деление — умножению и т. д. В предыдущей теме 8.1 рассмотрено новое действие — дифференцирование. Основной задачей дифференциального исчисления является нахождение производной или дифференциала заданной функции. Для дифференцирования существует обратное действие — интегрирование: нахождение функции по заданной ее производной или дифференциалу. Таким образом, если в процессе дифференцирования решается задача об отыскании скорости изменения функции, вызываемого изменением аргумента, то задачей интегрирования является нахождение самой функции по заданной скорости, ее изменения.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.5 (0.041 с.) |
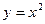 является первообразной для функции
является первообразной для функции 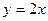 , т.к.
, т.к. 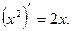
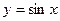 является первообразной для функции
является первообразной для функции 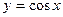 , т.к.
, т.к. 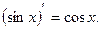
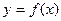
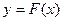
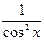
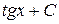
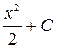
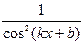
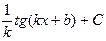
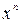
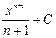
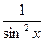
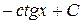
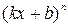
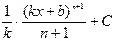
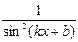
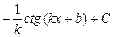
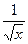
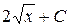
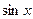
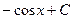
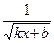
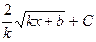
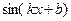
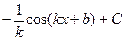
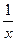
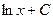
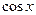
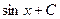
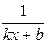
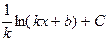
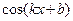
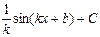
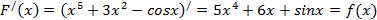
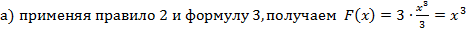
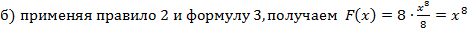
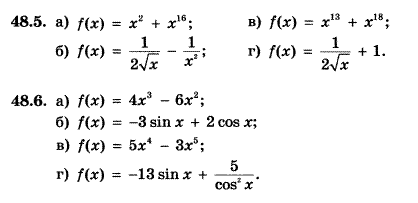
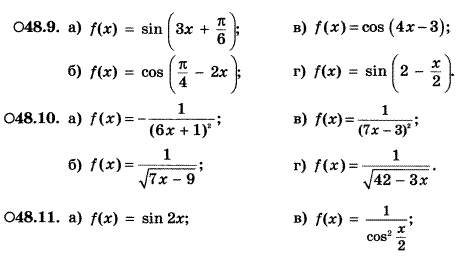
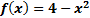 , график которой проходит через заданную точку
, график которой проходит через заданную точку 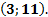
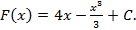
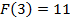 (3 и 11 – соответствующие координаты заданной точки).
(3 и 11 – соответствующие координаты заданной точки).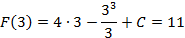
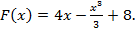
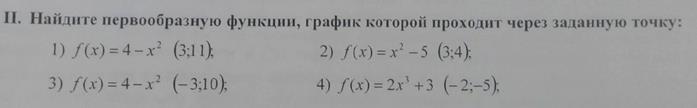 Реши самостоятельно по образцу: решить примеры под цифрой II
Реши самостоятельно по образцу: решить примеры под цифрой II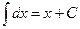 2.
2. 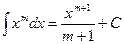 3.
3. 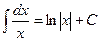
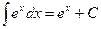 5.
5. 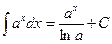 6.
6. 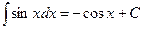
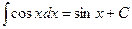 8.
8. 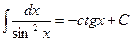 9.
9. 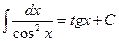
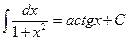 11.
11. 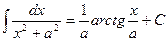 12.
12. 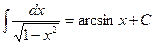
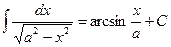 14.
14. 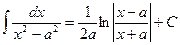
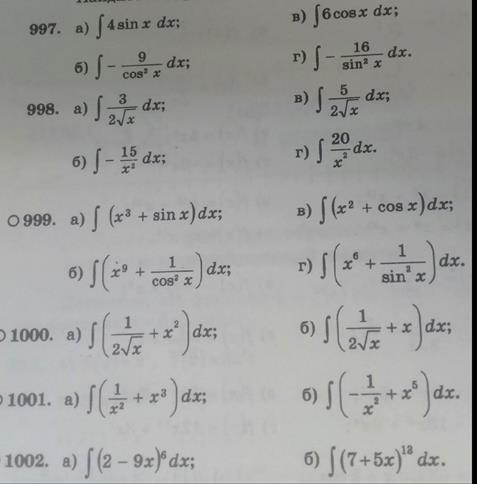
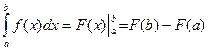 .
.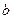 называются пределами интегрирования (а – нижний предел,
называются пределами интегрирования (а – нижний предел, 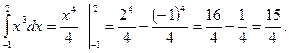
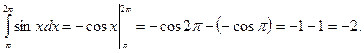
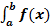 находят:
находят: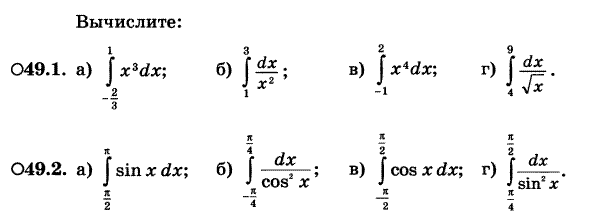
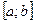 функции
функции 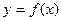 , осью ОХ и прямыми х = а и х =
, осью ОХ и прямыми х = а и х = 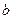 .
.
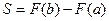 , где
, где 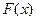 - первообразная для функции
- первообразная для функции 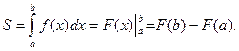

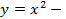 парабола, ветви которой направлены вверх (строим по точкам)
парабола, ветви которой направлены вверх (строим по точкам) прямые, параллельные оси OY.
прямые, параллельные оси OY.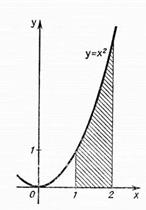

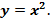
 .
. и
и 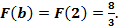
 .
.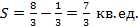

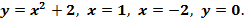
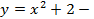 парабола, ветви которой направлены вверх (сдвиг по оси OY вверх на 2)
парабола, ветви которой направлены вверх (сдвиг по оси OY вверх на 2) прямые, параллельные оси OY.
прямые, параллельные оси OY.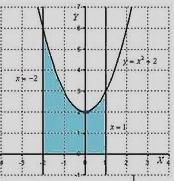
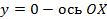

 .
.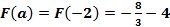 и
и