Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.Содержание книги
Поиск на нашем сайте
Дифференцируемая функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство F'(x) = f(x). Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной. Примеры: 1) функция 2) функция Как всякое обратное действие, интегрирование вносит некоторое осложнение. Вспомним, как начинается изучение действий над числами. Сначала изучают только целые положительные числа. Наиболее простое действие — сложение — не вносит никаких затруднений. Однако стоит только перейти к обратному действию вычитанию, как встречается первое затруднение: вычесть из меньшего числа большее невозможно. Чтобы преодолеть эту трудность, в алгебре вводят отрицательные числа и вычитание становится возможным. При умножении целых чисел не встречается никаких затруднений; обратное же действие — деление — сразу вносит трудность. Оказывается, что далеко не все числа делятся друг на друга. Деление становится возможным с введением дробных чисел. Еще большие затруднения появляются при извлечении корня — действии, обратном возведению числа в целую положительную степень; здесь уже появляются затруднения в знаках. Так, корень четной степени из положительного числа имеет два знака, а корень четной степени из отрицательного числа не имеет действительного значения. Чтобы стало возможным извлечение корней целой положительной степени из действительных чисел, требуется ввести понятия об иррациональном числе, о мнимой единице, о мнимом числе и т. д. Интегрирование как действие, обратное дифференцированию, также вносит осложнение. Дифференцирование функции — однозначная операция, т. е. если функция имеет производную, то только одну. Обратная операция — отыскание первообразной — не однозначна. Так, функции F1(x) = x4, F2(x) = x4 + 5, F3(х) = x4+C, где С — любое постоянное действительное число, являются первообразными функции f(х) = 4х3, поскольку все эти функции имеют одну и ту же производную. Если F(x) является первообразной функции f(х) на некотором промежутке, то множество всех первообразных этой функции имеет вид F(x)+С, где С — любое действительное число.
Таким образом, любые две первообразные данной функции отличаются друг от друга на постоянное слагаемое, а выражение F(x)+C исчерпывает множество всех первообразных заданной функции f(x). Итак, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений. Геометрически выражение F(x)+C представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси Оу.
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.241.201 (0.009 с.) |

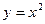 является первообразной для функции
является первообразной для функции 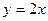 , т.к.
, т.к. 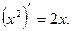
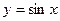 является первообразной для функции
является первообразной для функции 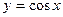 , т.к.
, т.к.