
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информационный аспект измерений.Содержание книги
Поиск на нашем сайте
Признаки измерения
Средство измерения обладает нормированными метрологическими характеристиками. Физическая величина – свойство общее в качественном отношении для многих физических объектов, процессов или явлений, но индивидуальное в количественном отношении. СИ: м, kg, c, A, ºK, моль Приблизительно – 2000 ФВ, измерить можно 600 ФВ. Измерение à истинное значение Ф.В. à действительное значение ФВ. Действительное значение ФВ – значение, которое удовлетворяет решению задачи в данном конкретной случае. Классификация ФВ
Пассивные – не могут совершать работу.
Случайные – изменяются по законам теории вероятности.
Квантованные – которые имеют конечное счетное количество значение в заданном диапазоне.
Дискретные (во времени)
t Объект измерения – модель Примеры:
- объект
R L
C
Виды измерений Виды измерений
1.1. Прямые измерения. y=f(x) – измерения при которых искомое значение определяется непосредственно в ходе эксперимента из опытных данных. 1.2. Косвенные измерения. y=f(x1,x2,x3,…xn) – используется известная функция, начальная зависимость м/д результатом измеренными прямым способом и искомой ФВ. 1.3. Совместные измерения. y=A0+A1x+A2x2 Производится одновременное измерение нескольких разноименных ФВ для нахождения зависимости м/д ними. 1.4. Совокупные измерения. Когда происходит одновременное измерение нескольких одноименных ФВ для определения искомых значений другой ФВ путем решения системы уравнений.
2.1. Статические измерения – измерения некоторой ФВ значение которой неизменна в течении времени использования результата. 2.2. Динамические измерения – измерения изменяются во времени величины.
3.1. Однократные (один раз и правильно) 3.2. Многократные
4.1. Равноточные – не изменяются условия проведения эксперимента, используются одни и те же приборы. 4.2. Неравноточные – условия могут изменяться и используются различные по уровню точности средства измерения.
Характеристики 1. Амплитудная (амплитудное значение) – наибольшее значение сигнала, близкое к мгновенному значению. хА=max x(t) 2. Среднее значение – усреднение сигнала за некоторый интервал времени. Используется для описания постоянной составляющей сигнала. xср=1/Т ∫т0 x(t) dt
T/2 T
В первом случае среднее значение – 0, во втором конкретное (не=0) значение. 3. Среднее выпрямленное значение – используется для характеристики симметричных относительно нулевой оси сигналов. xср.в.=1/Т ∫т0 |x(t)| dt 4. Среднеквадратическое значение (действующее) – используется для описания мощности сигнала. Хср.кв.=1/Т ∫т0 (x(t))2 dt=хд
Коэффициент амплитуды – ka=xA/xд Коэффициент формы сигнала – kф=xд/хср.в. Коэффициент усиления – kу=хА/хср.в.
Меандр
x(t)
Т/2 Т t
Значение на выходе электронных приборов – действительное значение
Методы измерений. В зависимости от использования меры, выделяют 2 метода.
Мера используется опосредованно, поскольку она использовалась при изготовлении этого средства измерения.
2.1 Нулевой метод. Метод заключается в том, что разность измеряемой величины и величины, воспроизводимой мерой в процессе измерения сводится к нулю, что фиксирует НИ. Результат равен U0. По данной схеме построены мостовые измерительные приборы. При высокой точности меры, метод позволяет получить результат с высокой точностью. 2.2 Дифференцированный метод. Данный метод позволяет получить результат с высокой точностью, при использовании сравнительно низко-точного СИ. Δ – абсолютная погрешность измерения вольтметром. Δ/ΔU – есть относительная погрешность Пусть Δ/ΔU=1% Возьмем и подберем меру т.о., чтобы ΔU/Ex≈1% Поскольку мера – средство измерения точно, то погрешностью U0 можно пренебречь. Относительная погрешность измеряемой величины Ex Δ/Ex≈0,01%
Погрешности измерений. Классификация. Примеры. Цель – измерение значения ФВ. Погрешность – разность м/д измеренной величиной и истинным значением (действующим значением) Δх=хизм – хист = хизм – хд хрез=хизм ± Δх Результат – значение измеренной величины ± погрешность Погрешность – количественная характеристика. Точность измерения – качественная характеристика, отражающая близость к нулю погрешности измерения.
Классификация погрешностей
1.1. Абсолютная погрешность Δ=хизм-хд – выражается в единицах измеряемой величины 1.2. Относительная погрешность. δ = Δ/хизм*100% Отношение абсолютной погрешности к измеренному значению, выражается, как правило, в %. 1.3. Приведенная погрешность. γ= Δ/хN*100% Отношение абсолютной погрешности к некоторому нормирующему значению – приведенная погрешность.
Только для описания СИ, т.к. xN - характеристика Си, которая определяется следующим образом. a) xN=xmax – предельное значение СИ данного диапазона.
b) xN = | - xmax| + | xmax| В общем случае -xmax<> xmax.
-xmax xmax c) xN=xmax, если нуля нет. xнач<>0
xнач xmax
1. Методическая погрешность – погрешность, возникающая из-за неадекватности принятой модели объекту измерения. 2. Инструментальная погрешность – приборная погрешность самого СИ
1. Систематическая погрешность - погрешность, которая постоянная или изменяется по известному закону. 2. Случайная погрешность - изменяется по закону случайных чисел. Для ее нахождения используются элементы теории вероятности – статистические измерения. 3. Промахи (грубая погрешность) – субъективная погрешность оператора.
1. Основная погрешность – возникает при нормальных условиях эксплуатации средства измерения. н.у. T(20ºC), p (760 мм рт. ст.), влажность (80%), э/м воздуха 2. Дополнительная погрешность – в условиях отличных от нормальных. В паспортах приборов указывается коэффициенты влияния, которые позволяют рассчитать изменения показаний в зависимости от изменения условий.
1. Статическая погрешность – возникает при измерении постоянной во времени величины 2. Динамическая погрешность – возникает при измерении сигнала, изменяющегося во времени.
tПо связи с измеряемой величиной. 3. Аддитивная погрешность – не зависит от измеряемой величины. Δx=a
4. Мультипликативная погрешность – зависит от измеряемой величины. Δx=bx
Когда у прибора есть и та и другая погрешности, то Δx=a+bx
Правила записи результатов По ГОСТу: х=хизм ± Δх Δх -? Погрешность 34570124 Инструментальная погрешность1% В окончательной записи погрешности останется один лил 2 знака. Если перед "5" стоит четная цифра, то она не изменяется. 34,570124 ≈ 34 δ1 = (34-34,570124)/34 *100%=1,7% <=10% Если погрешность не превышает 10%, то округлять можно. δ2 = (30-34,570124)/30 *100%=15,2%>10% Нельзя оставлять один знак.
Если первая цифра в результате погрешности 1 или 2, то в окончательной записи погрешности остается два знака. Если 4 и выше, то, как правило, остается один знак. Если 3, то в зависимости от того, что стоит дальше, оставляют один лили два знака. Δх= ±34 или Δх=(±3,4)*101 Результат измерения округляется до того же количества разрядов, до того же порядка. х=(178,56±34)*101 - неправильно х=(178,6±3,4)*101 - правильно
Законы распределения Нормальный закон распределения. Закон Гаусса.
σ2
квантили
σ1<σ1
Чем меньше СКО, тем точнее проведены измерения.
Равномерный закон распределения. В цифровых измерительных приборах.
-Δх1 Δх1 Δх
0, |Δх|>Δх1 W(Δх)= 1/(2Δх1), |Δх|<=Δх1
Трапециидальный закон – композиция нескольких равномерных.
-Δх2 -Δх1 Δх1 Δх2
Треугольный закон. Если границы равномерных совпадают.
-Δх1 Δх
Наиболее употребительным законом распределения является нормальный, т.к. по центральной предельной теореме т.в. несколько слагаемых со своими законами распределения дадут нормальный закон, если ни одно из них не преобладает.
Мосты и их характеристики.
Измерительные мосты. Строятся на основе метода сравнения с мерой. Для измерения R, C, L, θ, а также для измерения других физических величин, которые могут быть определены с их использованием. Мостовые схемы характеризуются высокой чувствительностью и высокой точностью. Подразделяются на: 1) мосты постоянного тока 2) мосты переменного тока 3) с ручным уравновешиванием 4) с автоматическим уравновешиванием
а,б – диагональ питания в,г – измерительная диагональ В измерительной диагонали используются либо нуль-индикаторы, либо средства измерения тока. z1, z2, z3, z4 – плечи моста
Ток в измерительной диагонали
Условие равновесия мостовой схемы: I0=0, при этом Z1Z4=Z2Z3. Произведение сопротивлений противоположных плеч моста равны между собой. Мост постоянного тока: R1R4=R2R3 Мост переменного тока:
Сходимость моста – достижение состояния равновесия определенным (конечным) числом поочередных переходов от регулировки одного параметра к другому. Мосты работающие в уравновешенном режиме, или в неуравновешенном.
НИ – Нуль-индикатор МЭГ – магнитоэлектрический гальванометр
В первом случае результат определяется из условия равновесия по значению плеч моста, а во втором результат измерения определяется показаниями амперметра или вольтметра. Чувствительность мостов
Чувствительность по напряжению.
Ограничением на увеличение напряжения питания с целью увеличения чувствительности являются ограничения по рассеиваемой мощности в плечах моста.
Для переменного тока.
Мост должен быть симметричным: Z1=Z2, Z3=Z4, а угол сдвига фаз моста равен π. Из-за наличия потерь в плечах моста выполняется лишь условное равенство θ≈±π. Постоянного тока.
ВД - Входной делитель с коэффициентом преобразования, УПТ - Усилитель постоянного тока, ИМ- Магнитоэлектрический измерительный механизм.
Обладают высокой чувствительностью. Особенности: 1) 1) 2) Большое входное сопротивление При Для увеличения чувствительности используется модулятор, демодулятор. (микровольтметры)
U~ - переменное напряжение Uвых – выходное напряжение M- модулятор Y~ - усилитель переменного тока ДМ - демодулятор Г – генератор Ux- измеряемое напряжение UM – модуляционное напряжение
Усилитель усиливает переменную составляющую.
Функцию модулятора и демодулятора выполняют аналоговые ключи, которые управляются генератором синхронно. Позволяет получать величину коэффициента усиления до ~10^5. Зависит от полярности. Универсальные вольтметры. На основе пиковых детекторов с закрытым входом. Постоянное напряжение: 0.1÷600В Переменное напряжение: 1÷600В Сопротивление: 10Ом÷100Мом
Импульсные вольтметры. Для измерения амплитуды сигналов различной формы. Особенности: 1) Малая длительность измеряемых импульсов 10÷100нс 2) U(t)
Шкала градуируется в амплитудных значениях. Пиковый детектор с закрытым входом. Селективные вольтметры. Для измерения действующих значений напряжения в некоторой полосе частот или действующего значения определенных гармоник.
Δ ω Полоса пропускания полосового фильтра выделяет одну отдельную гармонику k(ω)=k=const k(ω)=f – на всех остальных частотах
Реальная - это уже диапвзон частот Невысокая точность 6÷15% основная погрешность. Диапазон измеряемого напряжения0.1мкВ÷1В. Диапазон частот 10Гц÷100кГц.
Погрешность дискретности. 1) Измеряемая величина отождествляется с ближайшим большим или равным уровнем квантования.
tн tк
В общем случае – величина х –случайная, поэтому Δд – является также случайной величиной, распределенной по случайному закону.
1 2 3 4 хвх
2) С ближайшим меньшим или равным.
1 2 3 4 Δx=xki-x
1
-1
3) С ближайшим уровнем – если входная величина не превышала половины кванта, то на ближе к нижнему уровню, иначе к верхнему.
x Δxk/2
Погрешность квантования – методическая. Систематическая – мат ожидание.
Последовательность шагов. 1) Получение экспериментальных данных 2) Оценка мат ожидания 3) Оценка систематической погрешности 4) Исключение систематической погрешности из ряда наблюдений, т.е. получение исправленного ряда 5) Получение оценки измеряемой величины близкой к истинному значению 6) Определение оценки дисперсии случайной погрешности.S[x] Случай прямых измерений.
1. Дисперсия известна. 2. Дисперсия не известна, тогда по правилу обработки результата требуется определить оценку дисперсии S2[x]
- оценка дисперсии действительного значения
Для определения доверительного интервала погрешности необходимо определить закон распределения первой или второй дроби. Если xi распределен по нормальному закону, то закон распределения дроби также нормальный.
Для определения границ доверительного интервала надо взять табличные значения zp и tp а потом обратиться к выражениям
В случае, если закон распределения не нормальный, то увеличивают n и используют табличные значений доверительных интервалов.
Промах – значительно отличается от остальных значений. Критерий:
Если неравенства не выполняются то xk – промах и должно быть исключено из ряда наблюдений. Требуется повторный расчет
Два момента, накладывающие ограничение на размер выборки: 1) поскольку увеличение числа измерений влечет увеличение времени проведения эксперимента, то должна быть уверенность в том, что измеряемая величина не изменяется. 2) Изменение условий проведения измерительного эксперимента
Однократное измерение (n=1)
Как правило, все описания СИ содержат значения дисперсий.
Признаки измерения
Средство измерения обладает нормированными метрологическими характеристиками. Физическая величина – свойство общее в качественном отношении для многих физических объектов, процессов или явлений, но индивидуальное в количественном отношении. СИ: м, kg, c, A, ºK, моль Приблизительно – 2000 ФВ, измерить можно 600 ФВ. Измерение à истинное значение Ф.В. à действительное значение ФВ. Действительное значение ФВ – значение, которое удовлетворяет решению задачи в данном конкретной случае. Классификация ФВ
Пассивные – не могут совершать работу.
Случайные – изменяются по законам теории вероятности.
Квантованные – которые имеют конечное счетное количество значение в заданном диапазоне.
Дискретные (во времени)
t Объект измерения – модель Примеры:
- объект
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 x(t)
x(t)
 t
t
 x(t)
x(t)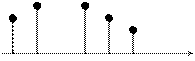


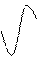 Модель - U~=Asinwt- переменная величина
Модель - U~=Asinwt- переменная величина


 Постоянный ток – R
Постоянный ток – R 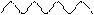
 R
R






 x(t)
x(t)

 t t'
t t'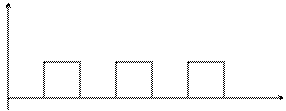


 0 xmax
0 xmax
 0
0
 Δx
Δx
 x
x
 Δx
Δx X
X
 Δx
Δx x
x
 Δхc<>0
Δхc<>0 
 W(Δх) σ1
W(Δх) σ1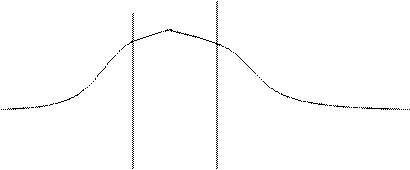
 -Δх1 Δхс +Δх2
-Δх1 Δхс +Δх2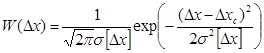
 W(Δх)
W(Δх)

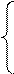
 W(Δх) Δх1<>Δх2
W(Δх) Δх1<>Δх2
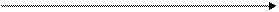 Δх
Δх W(Δх)
W(Δх)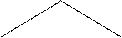
 Δх
Δх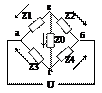
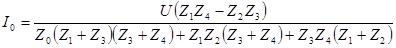
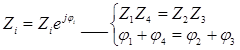



 В уравновеш. мосте – Z0 - НИ МЭГ -
В уравновеш. мосте – Z0 - НИ МЭГ - 



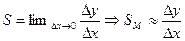
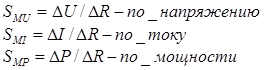
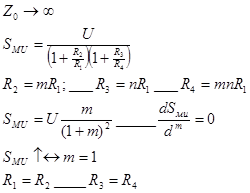
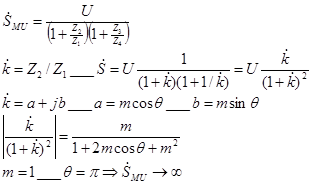

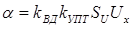
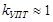
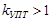 появляется дрейф нулевого уровня.
появляется дрейф нулевого уровня.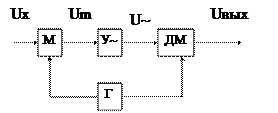

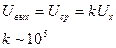









 Значительная скважность импульсов
Значительная скважность импульсов 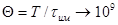 (период к длительности импульса)
(период к длительности импульса)
 t
t

 k(ω) идеальная
k(ω) идеальная



 реальная
реальная ω2 ω
ω2 ω
 ω1 ω3
ω1 ω3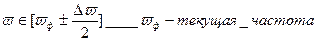
 x(t)
x(t) Δд
Δд

 t
t
 xп хп=хвх
xп хп=хвх

 45
45


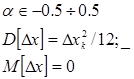
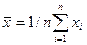 за оценку мат ожидания принимается среднее арифметическое значение результата измерения.
за оценку мат ожидания принимается среднее арифметическое значение результата измерения.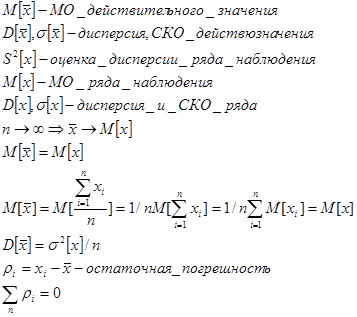
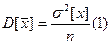
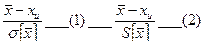
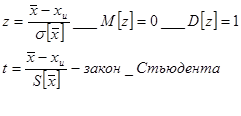
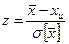 и
и 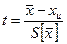
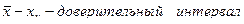
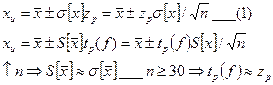
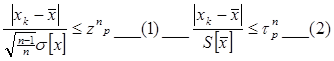
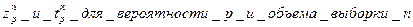
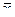 и всех его характеристик.
и всех его характеристик.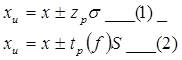 S – определяется по ранее поведенным экспериментам
S – определяется по ранее поведенным экспериментам


