Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индивидуальный проект по теме:Стр 1 из 4Следующая ⇒
Индивидуальный проект по теме: «Метод комплексных чисел» Автор работы: ученик 10 класса А Бирюков Никита, Научный руководитель: Чумичева О.В., учитель математики
ТАМБОВ 2019
Оглавление
Введение Задачи в геометрии могут быть довольно сложными, в таких задачах представить себе ход решения бывает затруднительно, а иногда вовсе непонятно отчего стоит отталкиваться, из-за чего возникают проблемы с выбором метода решения. Порой можно использовать простой метод, но в конечном итоге зайти в тупик. Во избежание таких ситуаций следует сначала выбрать стратегию для решения задачи (не решать «в лоб»), и, конечно, чем больше различных методов решения задач мы знаем, тем легче нам подобрать лучший способ решения. В олимпиадах школьников, на различных экзаменах зачастую нерешенными остаются именно геометрические задачи, что говорит о неутешительном уровне понимания этого курса школьниками. В основе проблемы лежит поверхностное понимание материала, часто некоторые полезные теоремы не используются, потому что попросту забыты. Также, например, довольно редко прибегают к весьма эффективному – векторному способу решения задач.
Вышеуказанный метод схож с объектом изучения данного проекта – с методом решения геометрических задач в поле комплексных чисел. Чем это интересно и почему имеет связь с векторным способом, мы узнаем в дальнейшем. Однако стоит сказать, что с его помощью мы сможем решать широкий спектр задач. Отсюда следует актуальность проекта. Действительно, изучив качественно новый метод, мы сможем решать то, что раньше казалось непосильно. Теперь мы можем определить цель проекта. Цель: изучить комплексный метод решения геометрических задач. Задачи: 1. Узнать историю комплексных чисел и метода решения задач с их помощью. 2. Изучить поле комплексных чисел. 3. Изучить основы метода. 4. Научиться решать задачи, пользуясь данным методом. 5. Провести параллели с векторным способом решения. 6. Составить сборник задач, решаемых методом комплексных чисел. В этом проекте мы откроем для себя новый способ решения геометрических задач, узнаем о комплексных числах и их истории. В качестве продукта проекта предположительно будет сборник задач по геометрии, с помощью которого можно освоить данный незаурядный и полезный метод.
Литературный обзор История комплексного числа Итальянский математик Дж. Кардано в 1545 г. Впервые обратился к числам новой природы. В то время Кардано называл их “чисто отрицательными” или “софистически отрицательными”, считал их бесполезными. В 1572 году вышла книга математика Р. Бомбелли, в которой он установил первые, базовые правила арифметических операций над такими числами, вплоть до извлечения из них корней третьей степени. Название “мнимые числа” было введено в 1637 году математиком и философом Рене Декартом, и лишь через 140 лет один из известнейших математиков того времени – Леонард Эйлер предложил использовать первую букву французского слова “imaginaire” (мнимый) для обозначения числа – 1, т. е. мнимой единицы. Это обозначение стало употребимо в широких кругах благодаря К.Гауссу. Сам Термин “комплексные числа” так же был введен им в 1831 году. Слово комплекс (лат. “complexus”) обозначает связь, сочетание, совокупность понятий, предметов, а также явлений – образующих единое целое.
В течение XVII века продолжалось обсуждение арифметики мнимых чисел, их геометрическое обоснование. В конце XVIII века французский математик Ж. Лагранж утвердил, что для математического анализа мнимые величины уже не являются чем-то затруднительным. С помощью мнимых чисел научились решать линейные дифференциальные уравнения с постоянными коэффициентами. Такого типа уравнения встречаются в теории колебаний материальной точки в сопротивляющейся среде. Также комплексные числа применялись в решении интегралов. Хотя в течение XVIII века с помощью комплексных чисел удалось решить многие вопросы, в том числе и прикладные задачи, связанные с гидродинамикой, картографией и т. д. (позднее и аэродинамикой), однако на тот момент еще не было строго логического обоснования теории комплексных чисел. В конце XVIII века, в начале следующего было создано геометрическое истолкование этих чисел. К.Вессель, Ж.Арган и К.Гаусс независимо друг от друга предложили изобразить комплексное число z = x + y × i точкой m (x, y) на координатной плоскости. Как оказалось радиус-вектор, соединяющий эту точку с точкой отсчета можно считать модулем комплексного числа, что к слову имеет большое значение в изучаемом методе. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. Стало понятно, что комплексные числа полезны в тех вопросах, где имеют дело с величинами, которые изображаются векторами на плоскости: при изучении задач теории упругости, течения жидкости. На этом же основывается изучаемый нами метод.
Коллинеарность векторов Для начала определимся с понятиями сонаправленных и противоположно направленных векторов. Если векторы сонаправлены, то углы образованные пересечением с действительной осью у таких векторов равны. Действительно, так как прямые их содержащие являются параллельными, то соответственные углы равны. На комплексной плоскости это означает, что для данных точек А(а) и В(b) векторы ОА и ОВ сонаправлены, если arg a = arg b (или arg a/b=0). Очевидно, если векторы противоположно направлены, то их углы будут отличаться не на 00, а на ±1800 или на ±π, то есть arg a/b=±π. Но числа с аргументами 0, ±π являются действительными (точки им соответствующие лежат на действительной оси). Отсюда получаем критерий коллинеарности точек А(а) и В(b) с точкой начала координат: необходимо и достаточно, чтобы a/b являлось действительным числом. Теперь возьмем точки А(a), B(b), D(d), C(c), рассмотрим критерий коллинеарности векторов ВА и DC. Их комплексные координаты а – b, c – d соответственно. Тогда получаем формулу:
То есть данное частное должно быть действительным числом.
Перпендикулярность векторов
То есть это частное является чисто мнимым числом.
Правильные многоугольники
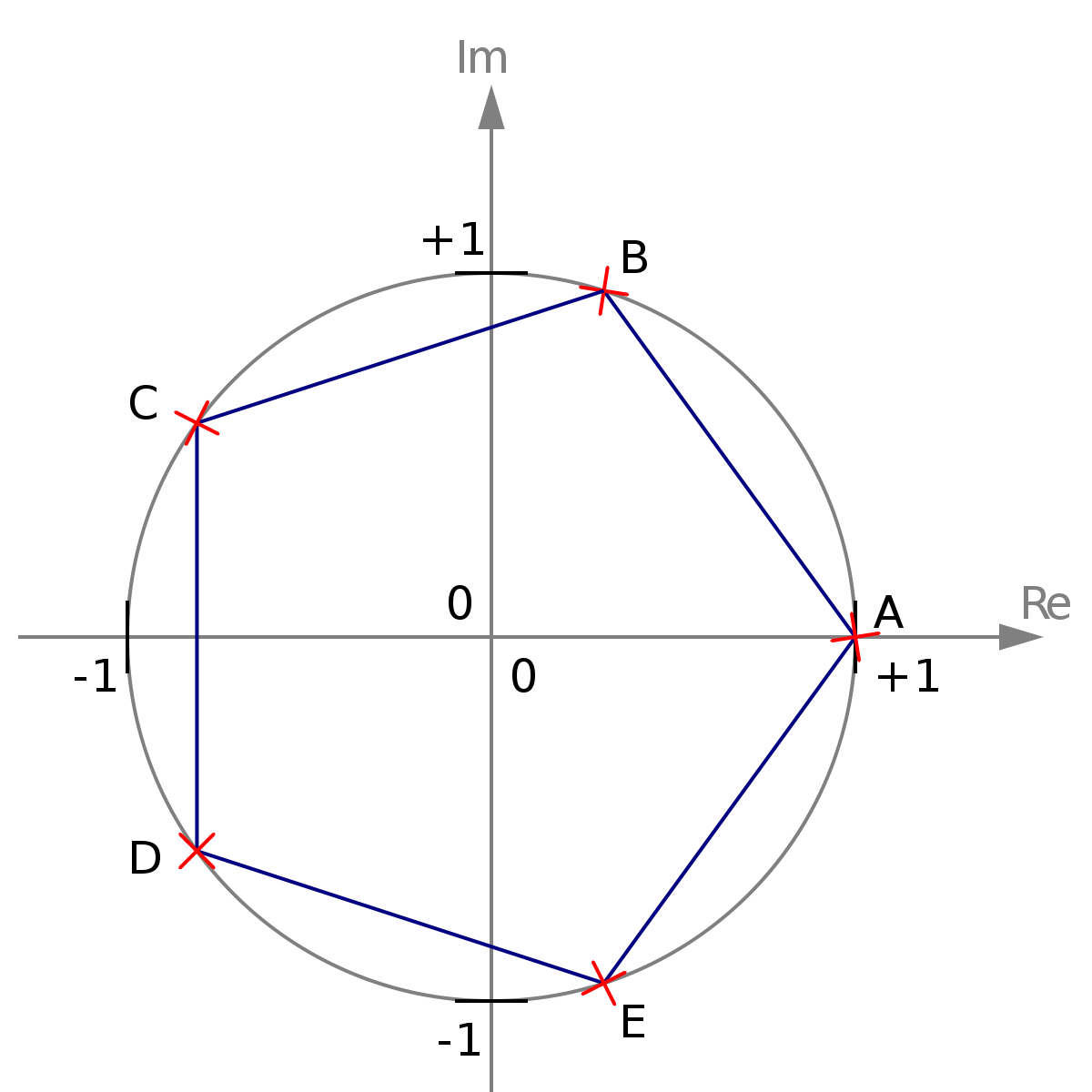
На рис. 4 изображен правильный пятиугольник, вершинами которого являются корни пятой степени из единицы. Для построения многоугольника необходимо найти все комплексные корни.
Рис. 4 При решении задач с правильными многоугольниками бывает удобно поместить центр многоугольника в начало координат, одну из его вершин в точку (1;0).
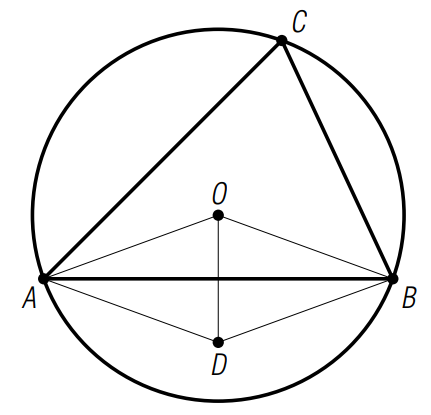
Примеры решения задач Задача 4.1 Точка D симметрична центру описанной около треугольника АВС окружности, относительно АВ. Доказать, что CD = R2 + AC2 + BC2 – AB2. Решение: примем точку О за точку начала координат, тогда уравнение этой окружности: z×z=R2. AOBD – ромб, так как расстояния от О до АВ и от D до АВ равны, OD перпендикулярен АВ. Но тогда OA + OB = OD, а через комплексные координаты а+b=d. Тогда получаем, что:
Рис. 5
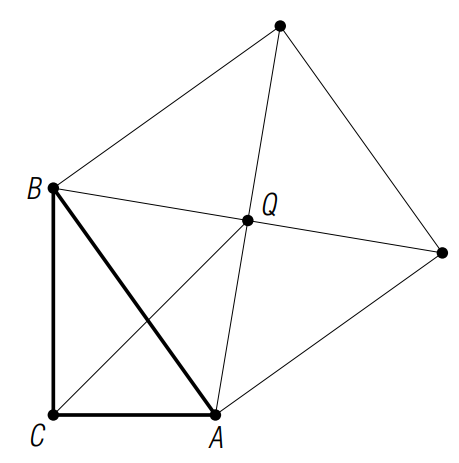
Получается, что левая и правая части равны одному и тому же, следовательно, они равны между собой. Что и требовалось доказать. Задача 4.2 На гипотенузе АВ прямоугольного треугольника АВС построен квадрат вне треугольника, найти расстояние от вершины С до центра квадрата, если ВС и АС соответственно равны а и b. Решение: для начала вспомним о геометрическом смысле произведения комплексных чисел. То есть, если мы b умножим на а, то получим поворот b на arg a. Получается, что а выступает в роли параметра, тогда если угол поворота равен 900, т.к. такой угол соответствует чисто мнимому числу, то а=i.
Пусть С является точкой начала координат, СА и СВ действительная и мнимая соответственно, т. е. А(b) и B(ai). Заметим, что BQ при повороте на 900 переходит в QA. Тогда, воспользовавшись ранее рассмотренным случаем, заключаем, что (ai –q)i=b – q, выделяем q и получаем:
Задача 4.3
Дан произвольный четырехугольник, не являющийся трапецией. Прямая соединяет середины противоположных сторон четырехугольника и образует с двумя другими его сторонами равные углы. Доказать, что эти прямые, составляющие равный угол с данной прямой, равны между собой.
Но по условию четырехугольник не трапеция, следовательно, AB не параллельно CD, следовательно, вторая скобка не может обратиться в 0. Тогда первая скобка обращается в 0, но отсюда следует, что AB=CD, ч.т.д.
Задача 4.4
Решение: Возьмем за точку M начало координат. Тогда m=0. Следовательно a0 = a1 – a, b0 = b1 – b, c0 = c1 – c. Отсюда получаем, что b0 – a0 = b1 – a1 – (b – a), c0 – a0 = c1 – a1 – (c – a).
Разделим на b – a и c – a соответственно:
Но по условию выражения в правых частях выражений равны, из чего следует, что:
Это означает подобие первого и третьего треугольников, очевидно, что в таком случае все эти треугольники подобны между собой.
Выводы В этой работе мы рассмотрели такой полезный и эффективный метод решения планиметрических задач. Смогли подробно, доведя до понимания, разобраться в фундаментальных аспектах комплексного метода. Мы научились решать задачи, используя данный незаурядный подход. Осознали тесную связь комплексного и векторного способов решения. Также на основе полученного опыта был составлен тематический сборник задач в качестве продукта. Безусловно, на первый взгляд, кажется, что использовать понятие несуществующего числа для решения геометрических задач подобно тому, как мы это делаем, используя векторы, абсолютно противоестественно. Однако порой благодаря этому способу решение задач упрощается достаточно сильно и решается в несколько действий. Действительно, этот метод весьма полезен и удивительно, что он почти всегда остается в тени.
В дальнейших планах расширить свои возможности в комплексном методе, глубже познать его, чтобы иметь возможность решать задачи качественно нового уровня.
Список литературы 1. Я.П. Понарин «Алгебра комплексных чисел в геометрических задачах» 2. «История развития комплексных чисел и их роль в науке и технике» интернет-портал https://articlekz.com 3. «Комплексные числа и их приложение к решению уравнений третьей и четвертой степени» интернет-портал http://textarchive.ru 4. Л.С. Атанасян, В. Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина «Геометрия. 7 – 9 классы» 5. М.Б. Балк, Г.Д. Балк, А.А. Полухин «Реальные применения мнимых чисел» Индивидуальный проект по теме: «Метод комплексных чисел» Автор работы: ученик 10 класса А Бирюков Никита, Научный руководитель: Чумичева О.В., учитель математики
ТАМБОВ 2019
Оглавление
Введение Задачи в геометрии могут быть довольно сложными, в таких задачах представить себе ход решения бывает затруднительно, а иногда вовсе непонятно отчего стоит отталкиваться, из-за чего возникают проблемы с выбором метода решения. Порой можно использовать простой метод, но в конечном итоге зайти в тупик. Во избежание таких ситуаций следует сначала выбрать стратегию для решения задачи (не решать «в лоб»), и, конечно, чем больше различных методов решения задач мы знаем, тем легче нам подобрать лучший способ решения. В олимпиадах школьников, на различных экзаменах зачастую нерешенными остаются именно геометрические задачи, что говорит о неутешительном уровне понимания этого курса школьниками. В основе проблемы лежит поверхностное понимание материала, часто некоторые полезные теоремы не используются, потому что попросту забыты. Также, например, довольно редко прибегают к весьма эффективному – векторному способу решения задач. Вышеуказанный метод схож с объектом изучения данного проекта – с методом решения геометрических задач в поле комплексных чисел. Чем это интересно и почему имеет связь с векторным способом, мы узнаем в дальнейшем. Однако стоит сказать, что с его помощью мы сможем решать широкий спектр задач. Отсюда следует актуальность проекта. Действительно, изучив качественно новый метод, мы сможем решать то, что раньше казалось непосильно. Теперь мы можем определить цель проекта. Цель: изучить комплексный метод решения геометрических задач. Задачи: 1. Узнать историю комплексных чисел и метода решения задач с их помощью. 2. Изучить поле комплексных чисел. 3. Изучить основы метода. 4. Научиться решать задачи, пользуясь данным методом. 5. Провести параллели с векторным способом решения. 6. Составить сборник задач, решаемых методом комплексных чисел. В этом проекте мы откроем для себя новый способ решения геометрических задач, узнаем о комплексных числах и их истории. В качестве продукта проекта предположительно будет сборник задач по геометрии, с помощью которого можно освоить данный незаурядный и полезный метод.
Литературный обзор История комплексного числа Итальянский математик Дж. Кардано в 1545 г. Впервые обратился к числам новой природы. В то время Кардано называл их “чисто отрицательными” или “софистически отрицательными”, считал их бесполезными. В 1572 году вышла книга математика Р. Бомбелли, в которой он установил первые, базовые правила арифметических операций над такими числами, вплоть до извлечения из них корней третьей степени. Название “мнимые числа” было введено в 1637 году математиком и философом Рене Декартом, и лишь через 140 лет один из известнейших математиков того времени – Леонард Эйлер предложил использовать первую букву французского слова “imaginaire” (мнимый) для обозначения числа – 1, т. е. мнимой единицы. Это обозначение стало употребимо в широких кругах благодаря К.Гауссу. Сам Термин “комплексные числа” так же был введен им в 1831 году. Слово комплекс (лат. “complexus”) обозначает связь, сочетание, совокупность понятий, предметов, а также явлений – образующих единое целое. В течение XVII века продолжалось обсуждение арифметики мнимых чисел, их геометрическое обоснование. В конце XVIII века французский математик Ж. Лагранж утвердил, что для математического анализа мнимые величины уже не являются чем-то затруднительным. С помощью мнимых чисел научились решать линейные дифференциальные уравнения с постоянными коэффициентами. Такого типа уравнения встречаются в теории колебаний материальной точки в сопротивляющейся среде. Также комплексные числа применялись в решении интегралов. Хотя в течение XVIII века с помощью комплексных чисел удалось решить многие вопросы, в том числе и прикладные задачи, связанные с гидродинамикой, картографией и т. д. (позднее и аэродинамикой), однако на тот момент еще не было строго логического обоснования теории комплексных чисел. В конце XVIII века, в начале следующего было создано геометрическое истолкование этих чисел. К.Вессель, Ж.Арган и К.Гаусс независимо друг от друга предложили изобразить комплексное число z = x + y × i точкой m (x, y) на координатной плоскости. Как оказалось радиус-вектор, соединяющий эту точку с точкой отсчета можно считать модулем комплексного числа, что к слову имеет большое значение в изучаемом методе. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. Стало понятно, что комплексные числа полезны в тех вопросах, где имеют дело с величинами, которые изображаются векторами на плоскости: при изучении задач теории упругости, течения жидкости. На этом же основывается изучаемый нами метод.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.90.44 (0.092 с.) |
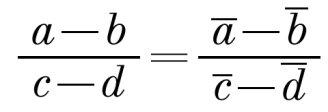
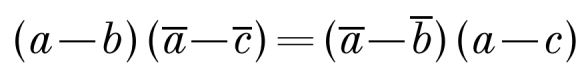 Как следствие определим условие коллинеарности для векторов имеющих общую точку, можно сказать условие принадлежности трех точек одной прямой. Для точек A(a), B(b) и C(c) формула примет вид:
Как следствие определим условие коллинеарности для векторов имеющих общую точку, можно сказать условие принадлежности трех точек одной прямой. Для точек A(a), B(b) и C(c) формула примет вид: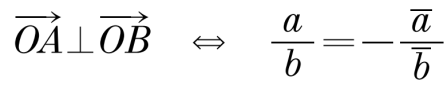 Рассуждения на тему перпендикулярных векторов весьма схожи с коллинеарностью векторов. Пусть даны точки A(a), B(b), тогда, если ОА перпендикулярен ОВ, то это означает, что arg a/b = ±π/2. Но комплексное число с аргументом ±π/2 является чисто мнимым.
Рассуждения на тему перпендикулярных векторов весьма схожи с коллинеарностью векторов. Пусть даны точки A(a), B(b), тогда, если ОА перпендикулярен ОВ, то это означает, что arg a/b = ±π/2. Но комплексное число с аргументом ±π/2 является чисто мнимым.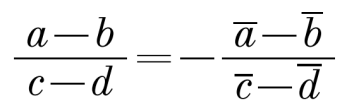 Для векторов не связанных с началом координат критерий перпендикулярности, аналогично предыдущему параграфу находится так:
Для векторов не связанных с началом координат критерий перпендикулярности, аналогично предыдущему параграфу находится так: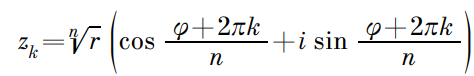 Данный аспект частично рассматривается в курсе алгебры за 10-11 класс. Построение правильного многоугольника тесно связано с нахождением корня n-ой степени из комплексного числа. Поскольку данная тема затрагивается в процессе изучения школьного курса, то не будем выводить формулу для нахождения корней из числа. Эта формула выглядит так:
Данный аспект частично рассматривается в курсе алгебры за 10-11 класс. Построение правильного многоугольника тесно связано с нахождением корня n-ой степени из комплексного числа. Поскольку данная тема затрагивается в процессе изучения школьного курса, то не будем выводить формулу для нахождения корней из числа. Эта формула выглядит так:
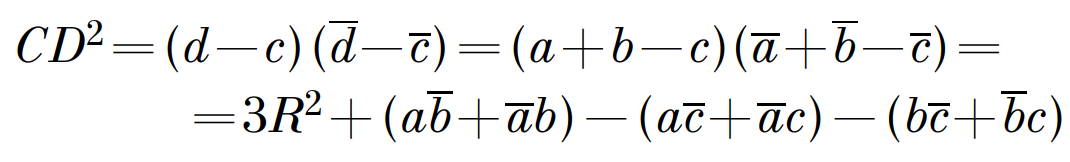
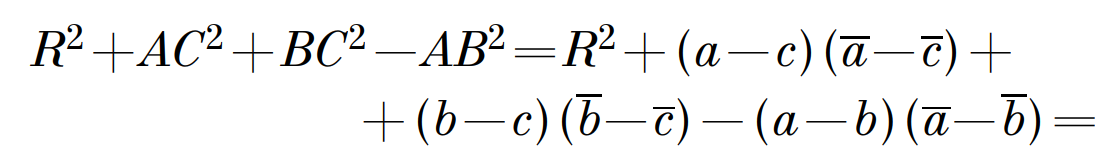 Но:
Но: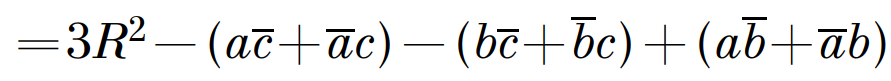
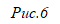 Теперь совершив основные приготовления, приступим к решению самой задачи.
Теперь совершив основные приготовления, приступим к решению самой задачи.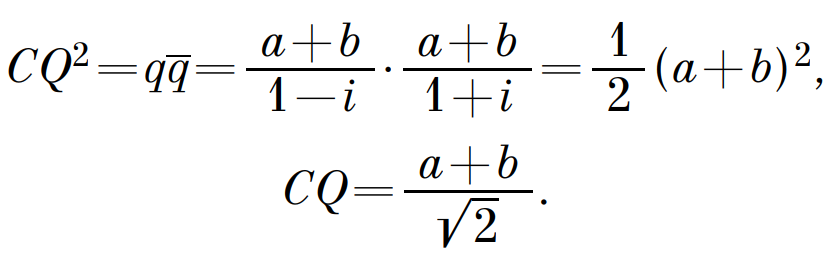
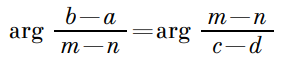
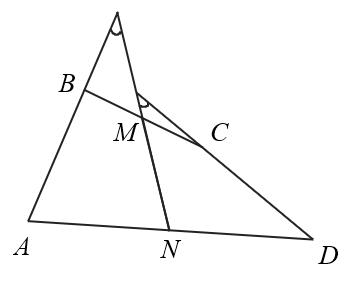 Решение: N и M – середины AD и BC. Углы между AB и MN и между CD и MN равны. Переходим к векторным величинам и выражаем их через комплексные координаты. Выражаем углы, используя алгебру комплексных чисел, так как эти углы равны по условию, то получаем:
Решение: N и M – середины AD и BC. Углы между AB и MN и между CD и MN равны. Переходим к векторным величинам и выражаем их через комплексные координаты. Выражаем углы, используя алгебру комплексных чисел, так как эти углы равны по условию, то получаем: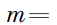
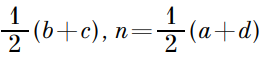 Переносим в левую часть и приравниваем к нулю. Из того, что аргумент равен 0, следует, что данное число является действительным. M и N делят противоположные стороны четырехугольника пополам, в методе комплексных чисел это значит, что:
Переносим в левую часть и приравниваем к нулю. Из того, что аргумент равен 0, следует, что данное число является действительным. M и N делят противоположные стороны четырехугольника пополам, в методе комплексных чисел это значит, что: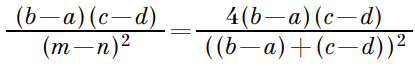 То есть:
То есть: 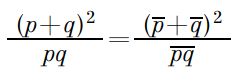
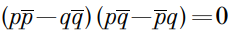 Для удобства обозначим b – a = p, c – d = q, тогда подставляя в полученное выражение, исходя из критерия принадлежности числа к множеству действительных чисел и используя свойства комплексно сопряженных чисел, имеем:
Для удобства обозначим b – a = p, c – d = q, тогда подставляя в полученное выражение, исходя из критерия принадлежности числа к множеству действительных чисел и используя свойства комплексно сопряженных чисел, имеем: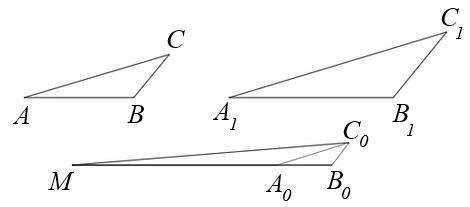 Два треугольника ΔABC и ΔA1B1C1 подобны. МА0, МВ0, МС0 соответственно равны АА1, ВВ1, СС1, причем точка М – произвольная. Доказать, что ΔА0В0С0 подобен данным.
Два треугольника ΔABC и ΔA1B1C1 подобны. МА0, МВ0, МС0 соответственно равны АА1, ВВ1, СС1, причем точка М – произвольная. Доказать, что ΔА0В0С0 подобен данным.