
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление отрезка в данном отношении
Если λ=1, то С – середина отрезка и равенство принимает вид: с=0,5(a+b).
Расстояние между двумя точками и уравнение окружности Длину отрезка можно определить аналогично тому, как это выполняется с помощью векторов. Если А(а), В(b), то АВ=ВА=|a–b|.
Тогда квадрат длины можно представить так:
Скалярное произведение векторов
То есть: .
Теперь, используя формулу скалярного произведения радиус-векторов, получаем:
Коллинеарность векторов Для начала определимся с понятиями сонаправленных и противоположно направленных векторов. Если векторы сонаправлены, то углы образованные пересечением с действительной осью у таких векторов равны. Действительно, так как прямые их содержащие являются параллельными, то соответственные углы равны. На комплексной плоскости это означает, что для данных точек А(а) и В(b) векторы ОА и ОВ сонаправлены, если arg a = arg b (или arg a/b=0). Очевидно, если векторы противоположно направлены, то их углы будут отличаться не на 00, а на ±1800 или на ±π, то есть arg a/b=±π. Но числа с аргументами 0, ±π являются действительными (точки им соответствующие лежат на действительной оси). Отсюда получаем критерий коллинеарности точек А(а) и В(b) с точкой начала координат: необходимо и достаточно, чтобы a/b являлось действительным числом. Теперь возьмем точки А(a), B(b), D(d), C(c), рассмотрим критерий коллинеарности векторов ВА и DC. Их комплексные координаты а – b, c – d соответственно. Тогда получаем формулу:
То есть данное частное должно быть действительным числом.
Перпендикулярность векторов
То есть это частное является чисто мнимым числом.
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.62.45 (0.004 с.) |
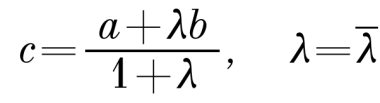 Пусть точка С делит отрезок АВ в отношении λ. Тогда АС = λ×СВ. Это равенство эквивалентно равенству ОС–ОА = λ×(ОВ–ОС), в комплексных координатах с – а = λ×(b–c). Решаем относительно с и получаем:
Пусть точка С делит отрезок АВ в отношении λ. Тогда АС = λ×СВ. Это равенство эквивалентно равенству ОС–ОА = λ×(ОВ–ОС), в комплексных координатах с – а = λ×(b–c). Решаем относительно с и получаем: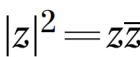 Зная квадрат модуля числа и произведение комплексно сопряженных чисел, получаем:
Зная квадрат модуля числа и произведение комплексно сопряженных чисел, получаем: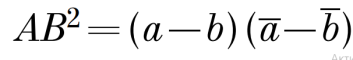
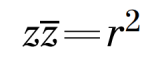 Пусть некоторое число z = x + y×i, произведение этого числа на сопряженное равно х2+у2. Тогда уравнение для окружности с центром в начале координат и радиусом r можно записать так:
Пусть некоторое число z = x + y×i, произведение этого числа на сопряженное равно х2+у2. Тогда уравнение для окружности с центром в начале координат и радиусом r можно записать так: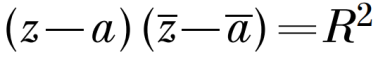 Для окружности с центром в некоторой точке А(а) уравнение выглядит так:
Для окружности с центром в некоторой точке А(а) уравнение выглядит так: Пусть имеются точки А(а) и В(b). Найдем скалярное произведение векторов ОА×ОВ:
Пусть имеются точки А(а) и В(b). Найдем скалярное произведение векторов ОА×ОВ:
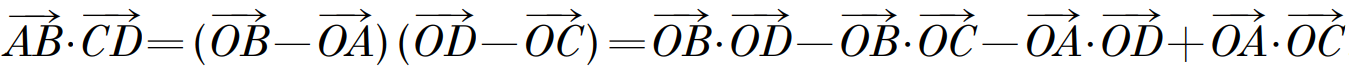 Теперь рассмотрим скалярное произведение не радиус-векторов. Пусть имеются также точки С(с) и D(d). Скалярное произведение АВ×СD:
Теперь рассмотрим скалярное произведение не радиус-векторов. Пусть имеются также точки С(с) и D(d). Скалярное произведение АВ×СD: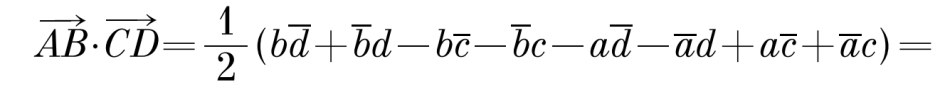
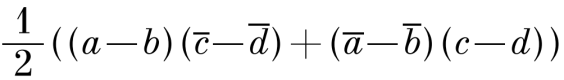
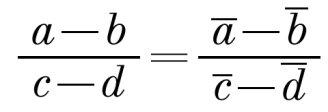
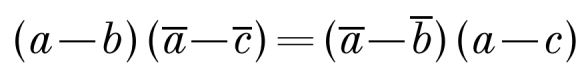 Как следствие определим условие коллинеарности для векторов имеющих общую точку, можно сказать условие принадлежности трех точек одной прямой. Для точек A(a), B(b) и C(c) формула примет вид:
Как следствие определим условие коллинеарности для векторов имеющих общую точку, можно сказать условие принадлежности трех точек одной прямой. Для точек A(a), B(b) и C(c) формула примет вид: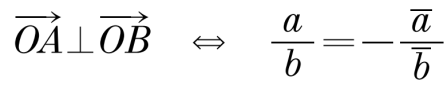 Рассуждения на тему перпендикулярных векторов весьма схожи с коллинеарностью векторов. Пусть даны точки A(a), B(b), тогда, если ОА перпендикулярен ОВ, то это означает, что arg a/b = ±π/2. Но комплексное число с аргументом ±π/2 является чисто мнимым.
Рассуждения на тему перпендикулярных векторов весьма схожи с коллинеарностью векторов. Пусть даны точки A(a), B(b), тогда, если ОА перпендикулярен ОВ, то это означает, что arg a/b = ±π/2. Но комплексное число с аргументом ±π/2 является чисто мнимым.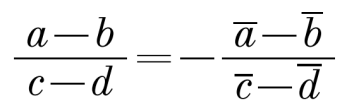 Для векторов не связанных с началом координат критерий перпендикулярности, аналогично предыдущему параграфу находится так:
Для векторов не связанных с началом координат критерий перпендикулярности, аналогично предыдущему параграфу находится так:


