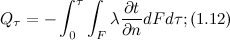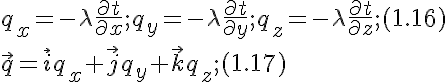Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тепловой поток. Закон фурье. Коэффициент теплопроводности.
Необходимым условием распространения теплоты является неравномерность распределения температуры в рассматриваемой среде. Таким образом, для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента в различных точках тела. Согласно гипотезе Фурье количество теплоты Вектор плотности теплового потока q направлен по нормали к изотерической поверхности. Его положительное направление совпадает с направлением убывания температуры, так как теплота всегда передаётся от более горячих частей к холодным. Таким образом, векторы q и gradt лежат на одной прямой, но направлены в противоположные стороны. Это и объясняет наличие знака "минус" в правых частях уравнений (1.9) и(1.8). Линии, касательные к которым совпадают с направлением вектора
Скалярная величина вектора плотности теплового потока q, Вт/м2, будет равна:
Самой большой плотностью теплового потока будет та, которая рассчитана вдоль нормали к изотермическим поверхностям. Если такой поток спроектировать на координатные оси Ox, Oy, Oz, то согласно уравнению (1.7):
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.211.87 (0.004 с.) |
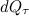 , Дж, проходящее через элемент изотермической поверхности dF за промежуток времени
, Дж, проходящее через элемент изотермической поверхности dF за промежуток времени 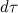 , пропорционально температурному градиенту
, пропорционально температурному градиенту 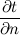 :
: 
 . Опытным путём установлено, что коэффициент пропорциональности в уравнении есть физический параметр вещества. Он характеризует способность вещества проводить и называется коэффициентом теплопроводности. Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности,
. Опытным путём установлено, что коэффициент пропорциональности в уравнении есть физический параметр вещества. Он характеризует способность вещества проводить и называется коэффициентом теплопроводности. Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности, 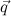 , Вт/м2, называется плотностью теплового потока:
, Вт/м2, называется плотностью теплового потока: 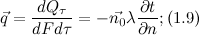
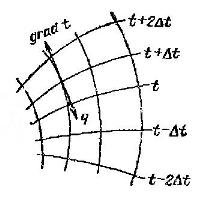
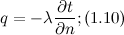 Многочисленные опыты подтвердили справедливость гипотезы Фурье. Поэтому уравнение (1.8), так же как уравнение, является математической записью основного закона теплопроводности, который формулируется следующим образом: плотность теплового потока пропорциональна градиенту температуры. Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком. Если градиент температуры для различных точек изотермической поверхности различен, то количество теплоты, которое пройдёт через всю изотермическую поверхность в единицу времени:
Многочисленные опыты подтвердили справедливость гипотезы Фурье. Поэтому уравнение (1.8), так же как уравнение, является математической записью основного закона теплопроводности, который формулируется следующим образом: плотность теплового потока пропорциональна градиенту температуры. Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком. Если градиент температуры для различных точек изотермической поверхности различен, то количество теплоты, которое пройдёт через всю изотермическую поверхность в единицу времени: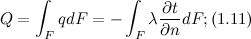 где dF - элемент изотерической поверхности. Значения измеряются в ваттах. Полное количество теплоты
где dF - элемент изотерической поверхности. Значения измеряются в ваттах. Полное количество теплоты 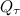 , Дж, прошедшее за время
, Дж, прошедшее за время  через изотермическую поверхность F, равно:
через изотермическую поверхность F, равно: