Этот МП-автомат уже был рассмотрен выше.

Работу данного МП-автомата можно неформально описать следующим образом:

· если на верхушке стека автомата находится нетерминальный символ А, то его можно заменить на цепочку символов a, если в грамматике языка есть правило А®a, не сдвигая при этом считывающую головку автомата (этот шаг работы на­зывается «подбор альтернативы»);

· если же на верхушке стека находится терми­нальный символ а, который совпадает с текущим символом входной цепочки, то этот символ можно выбросить из стека и передвинуть считывающую головку на одну позицию вправо (этот шаг работы называется «выброс»).

Данный МП-ав­томат может быть недетерминированным, поскольку при подборе альтернативы в грамматике языка может оказаться более одного правила вида А®a, следо­вательно, тогда функция d(q,l,A) будет содержать более одного следующего со­стояния — у автомата будет несколько альтернатив.

Данный МП-автомат строит левосторонние выводы для грамматики G(VT, VN, P,S). Для моделирования такого автомата необходимо, чтобы грамматика G(VT,VN,P,S) не была леворекурсивной (в противном случае, очевидно, автомат мо­жет войти в бесконечный цикл). Поскольку, как было доказано выше, произволь­ную КС-грамматику всегда можно преобразовать к нелеворекурсивному виду, то этот алгоритм применим для любой КС-грамматики, следовательно,им можно распознавать цепочки любого КС-языка.

Рассмотренный МП-автомат строит левосторонние выводы и читает цепочку входых символов слева направо. Поэтому для него естественным является построение дерева вывода сверху вниз. Такой распознаватель называется нисходящим.

 

 

Вопрос 19

Грамматики предшествования (основные принципы)

Еще одним распространенным классом КС-грамматик, для которых возмож­но построить восходящий распознаватель без возвратов, являются грамматики предшествования. Так же как и распознаватель рассмотренных выше LR-грамматик, распознаватель для грамматик предшествования строится на основе алго­ритма «сдвиг-свертка» («перенос-свертка»), который в общем виде был рассмот­рен в разделе «Распознаватели КС-языков с возвратом».

Принцип организации распознавателя входных цепочек языка, заданного грам­матикой предшествования, основывается на том, что для каждой упорядоченной пары символов в грамматике устанавливается некоторое отношение, называемое отношением предшествования. В процессе разбора входной цепочки расширен­ный МП-автомат сравнивает текущий символ входной цепочки с одним из сим­волов, находящихся на верхушке стека автомата. В процессе сравнения проверя­ется, какое из возможных отношений предшествования существует между этими двумя символами. В зависимости от найденного отношения выполняется либо сдвиг (перенос), либо свертка. При отсутствии отношения предшествования ме­жду символами алгоритм сигнализирует об ошибке.

Задача заключается в том, чтобы иметь возможность непротиворечивым образом определить отношения предшествования между символами грамматики. Если это возможно, то грамматика может быть отнесена к одному из классов грамматик предшествования.

Существует несколько видов грамматик предшествования. Они различаются по тому, какие отношения предшествования в них определены и между какими ти­пами символов (терминальными или нетерминальными) могут быть установле­ны эти отношения. Кроме того, возможны незначительные модификации функ­ционирования самого алгоритма «сдвиг-свертка» в распознавателях для таких грамматик (в основном на этапе выбора правила для выполнения свертки, когда возможны неоднозначности) [5, 6, 23, 65].

Выделяют следующие виды грамматик предшествования:

· простого предшествования;

· расширенного предшествования;

· слабого предшествования;

· смешанной стратегии предшествования;

· операторного предшествования.

 

 

Вопрос 20

Распознаватель на основе алгоритма «сдвиг-свертка»

Этот распознаватель строится на основе расширенного МП-автомата с одним состоянием q: R({q}, V, Z,d,q,S,{q}). Автомат распознает цепочки КС-языка, задан­ного КС-грамматикой G(VT,VN,P,S). Входной алфавит автомата содержит тер­минальные символы грамматики: V = VT; а алфавит магазинных символов стро­ится из терминальных и нетерминальных символов грамматики: Z = VT È VN.

Начальная конфигурация автомата определяется так: (q,a,l) — автомат пребыва­ет в своем единственном состоянии q, считывающая головка находится в начале входной цепочки символов aÎ VT *, стек пуст.

Конечная конфигурация автомата определяется так: (q,l,S) — автомат пребывает в своем единственном состоянии q, считывающая головка находится за концом входной цепочки символов, в стеке лежит символ, соответствующий целевому символу грамматики S. Функция переходов МП-автомата строится на основе правил грамматики:

1. (q,A)Îd(q,l,g), AÎ VN, gÎ(VT È VN)*, если правило А®g содержится во мно­жестве правил Р грамматики G: А®g Î Р.

2. (q,a)Îd(q,a,l) "aÎVT.

Неформально работу этого расширенного автомата можно описать так: если на верхушке стека находится цепочка символов g, то ее можно заменить на нетер­минальный символ А, если в грамматике языка существует правило вида А®g, не сдвигая при этом считывающую головку автомата (этот шаг работы называет­ся «свертка»); с другой стороны, если считывающая головка автомата обозревает некоторый символ входной цепочки а, то его можно поместить в стек, сдвинув при этом головку на одну позицию вправо (этот шаг работы называется «сдвиг» или «перенос»). Сам алгоритм, моделирующий работу такого расширенного ав­томата, называется алгоритмом «сдвиг-свертка» или «перенос-свертка» (по на­званиям основных действий алгоритма).

Данный расширенный МП-автомат строит правосторонние выводы для грам­матики G(VT, VN, P,S). Для моделирования такого автомата необходимо, чтобы грамматика G(VT, VN, P,S) не содержала l.-правил и цепных правил (в против­ном случае, очевидно, автомат может войти в бесконечный цикл из сверток). По­скольку, как было доказано выше, произвольную КС-грамматику всегда можно преобразовать к виду без l-правил и цепных правил, то этот алгоритм применим для любой КС-грамматики, следовательно, им можно распознавать цепочки любого КС-языка.

Этот расширенный МП-автомат строит правосторонние выводы и читает цепоч­ку входных символов слева направо. Поэтому для него естественным является построение дерева вывода снизу вверх. Такой распознаватель называется восхо­дящим.

Преимущество у данного алгоритма то же, что и у алгоритма нисходящего раз­бора с возвратами — простота реализации. Поэтому и использовать его можно практически в тех же случаях — когда известно, что длина исходной цепочки символов заведомо не будет большой (не больше нескольких десятков симво­лов).

Этот алгоритм также универсален. На его основе можно распознавать входные цепочки языка, заданного любой КС-грамматикой, достаточно лишь преобразо­вать ее к приведенному виду (а это можно сделать с любой грамматикой, см. раз­дел «Преобразование КС-грамматик. Приведенные грамматики»), чтобы она не содержала цепных правил и l-правил.

Сам по себе алгоритм «сдвиг-свертка» с возвратами не находит применения в ре­альных компиляторах. Однако его базовые принципы лежат в основе многих восходящих распознавателей, строящих правосторонние выводы и работающих без использования возвратов. Методы, позволяющие строить такие распознава­тели для некоторых классов КС-языков, рассмотрены далее. Эти распознаватели будут более эффективны в смысле потребных вычислительных ресурсов, но ал­горитмы их работы уже сложнее, кроме того, они не являются универсальными. В тех случаях, когда удается дать однозначные ответы на поставленные выше три вопроса о выполнении сдвига (переноса) или свертки при моделировании данного алгоритма, он оказывается очень удобным и полезным.

В принципе два рассмотренных алгоритма — нисходящего и восходящего разбо­ра с возвратами — имеют схожие характеристики по потребным вычислитель­ным ресурсам и одинаково просты в реализации. То, какой из них лучше взять для реализации простейшего распознавателя в том или ином случае, зависит прежде всего от грамматики языка. Вопрос о выборе типа распознавателя — нис­ходящий либо восходящий — достаточно сложен. В компиляторах на него кроме структуры правил грамматики языка влияют и другие факторы, например, необ­ходимость локализации ошибок в программе, а также то, что предложения всех языков программирования строятся в нотации «слева направо». Этот вопрос будет затронут далее, при рассмотрении других вариантов распознавателей для КС-языков; пока же эти два типа распознавателей можно считать сопоставимы­ми по эффективности (отметим — низкой эффективности) своей работы и про­стоте реализации.

 

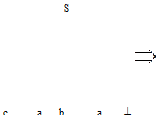
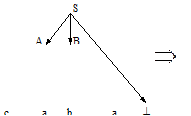
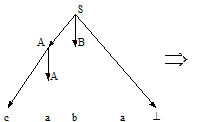
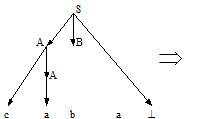
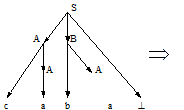
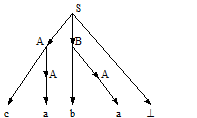
Вопрос 21

Метод рекурсивного спуска

Алгоритмы анализа, расходующие на обработку входной цепочки линейное время, применимы только к некоторым подклассам КС-грамматик. Рассмотрим один из таких методов.

Пример: пусть дана грамматика G =({a,b,c, ^}, {S,A,B}, P, S), где

P: S ® AB^

       A ® a | cA

       B ® bA

и надо определить, принадлежит ли цепочка caba языку L(G).

Построим вывод этой цепочки:

S ® AB^ ® cAB^ ® caB^ ® cabA^ ® caba^

Следовательно, цепочка принадлежит языку L(G). Последовательность применений правил вывода эквивалентна построению дерева разбора методом "сверху вниз":

Метод рекурсивного спуска (РС-метод) реализует этот способ практически "в лоб": для каждого нетерминала грамматики создается своя процедура, носящая его имя; ее задача - начиная с указанного места исходной цепочки найти подцепочку, которая выводится из этого нетерминала. Если такую подцепочку считать не удается, то процедура завершает свою работу вызовом процедуры обработки ошибки, которая выдает сообщение о том, что цепочка не принадлежит языку, и останавливает разбор. Если подцепочку удалось найти, то работа процедуры считается нормально завершенной и осуществляется возврат в точку вызова. Тело каждой такой процедуры пишется непосредственно по правилам вывода соответствующего нетерминала: для правой части каждого правила осуществляется поиск подцепочки, выводимой из этой правой части. При этом терминалы распознаются самой процедурой, а нетерминалы соответствуют вызовам процедур, носящих их имена.

Вопрос 22

Польская форма записи. Существуют три вида записи выражений:

· инфиксная форма, в которой оператор расположен между операндами (например, "а+b");

· постфиксная форма, в которой оператор расположен после операндов (то же выражение выглядит как "а b + ");

· префиксная форма, в которой оператор расположен перед операндами ("+ а b").

Постфиксная и префиксная формы образуют т.н. польскую форму записи. Польская форма удобна прежде всего тем, что в ней отсутствуют скобки. На практике наиболее часто используется постфиксная форма. Поэтому под польской обычно понимают именно постфиксную форму записи.

В этой форме записи выражение i=(a+b)*c выглядит так: " iab+c*=". Это выражение удобно расписывается по дереву: с нижней строки записываются “a” и “b”, далее “+” и “с”, выше – “i” и “*” и в вершине дерева “=”.

Тетрада - это четверка, состоящая из кода операции, приемника и двух операндов. Если требуется не два, а менее операторов, то в этом случае тетрада называется вырожденной. Например:

Исходное выражение	Код	Приемник	Операнд1	Операнд2
a+b®T1	+	Т1	а	b
T1+c®T2	*	T2	T1	c
i=T2	=	I	T2	(вырожденная тетрада)

 

Польская форма записи и тетрады удобны своей однозначностью. Фактически в обеих этих формах мы раскладываем исходное выражение на элементарные составляющие.

Пусть на вход синтаксического анализатора подаются выражения

"<ид1>=(<ид2>+<ид3>)*<ид4>" и "A = B+C*D"

На выходе будем иметь:

 

1) Дерево для выражения                            Дерево для выражения

"<ид1>=(<ид2>+<ид3>)*<ид4>"                                      "A = B+C*D"

2) Тетрады для "<ид1> = (<ид2>+<ид3>)*<ид4>"

+, <ид2>, <ид3>, T1

*, T1, <ид4>, T2

=, T2, <ид1>

Тетрады для "A = B+C*D"

*, C, D, T1

+, B, T1, T2

=, T2, A

(T1, T2 - временные переменные, созданные компилятором)

3) Польская форма для "<ид1> = (<ид2>+<ид3>)*<ид4>":

<ид1> <ид2> <ид3> + <ид4> * =

Польская форма для "A=B+C*D" будет выглядеть как "ABCD*+=". Обратите внимание на то, что порядок следования операндов в польской форме записи такой же, как и в исходном инфиксном выражении (записи abc *= и bc * a = - это вовсе не одно и то же).

Алгоритм вычисления польской формы записи очень прост:

Просматриваем последовательно символы входной цепочки. Если очередной символ является операндом (идентификатором или константой), то читаем дальше. Если символ является бинарным оператором, то извлекаем из цепочки два предыдущих операнда вместе с оператором, производим операцию и помещаем результат обратно в цепочку символов.

 

 

Вопрос 23