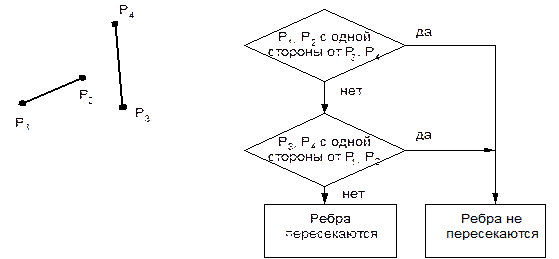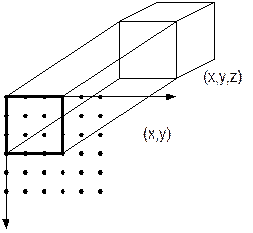Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы удаления скрытых линий и поверхностейСодержание книги
Поиск на нашем сайте
Предположим, что заданы трехмерный объект и видовые параметры, описывающие тип проекции, проекционную (картинную) плоскость и т.д., и требуется определить, какие ребра и поверхности объекта видимы, если смотреть из центра проекции (для центральных проекций) или вдоль направления проецирования (для параллельных проекций). Только эти ребра и поверхности мы и будем выводить на экран. Несмотря на простоту постановки, эта задача одна из самых сложных в машинной графике. Сложность привела к появлению большого числа алгоритмов (многие узкоспециализированные, разработаны в 60-70 гг.). Наилучшего решения нет. Для системы реального времени ‑ быстрые алгоритмы. Для мультипликации сложных реалистичных изображений – алгоритмы, учитывающие сложные эффекты: тени, проекции, фактуру ‑ очень медленные. Чем детальнее изображение, тем медленнее алгоритм. Все алгоритмы можно разделить на 2 группы: 1. Работающие в пространстве объекта (м. с. к.). 2. Работающие в пространстве изображения (ф. с. к., г. с. к.). 1. Каждая грань из n сравнивается с остальными (n-1) гранями => n2 проверок, это может быть меньше при малых n (n =1000, 1 млн проверок), но на каждый шаг алгоритма тратится очень много времени. 2. Объект – это множество граней, необходимо определить, видна ли каждая грань в каждой точке экрана (т.е. ближе к наблюдателю), следовательно, для каждой точки экрана (N) нужно проверить каждую грань => (N·n) проверок (если N =640 · 480=307 тыс., то 307 млн проверок), но такой подход более эффективен из-за простоты проверки.
2.1. Алгоритм сортировки по глубине Основная идея алгоритма художника: отсортировать многоугольники (грани объектов) в соответствии с их удаленностью от точки наблюдения, затем разместить многоугольники (раскладывая их в растр) в порядке убывания расстояния, т.е. ближние многоугольники помещаются в буфер кадра последними и закрашивают дальние. Аналогичен способу создания картины художником: рисуется фон, предметы дальнего, среднего и, наконец, переднего плана. Простой, но ресурсоемкий алгоритм с избыточным выводом графической информации. Алгоритм Ньюэл М., Ньюэл Р., Санча: 1. Упорядочить все многоугольники в соответствии с max Z-координаты. {P}
2. Разрешить все неопределенности с Z-оболочками и сформировать окончательный список (из которого будут исключены невидимые многоугольники). 3. Преобразовать каждый из многоугольников в растровую форму в порядке убывания Z-координаты (можно методами заполнения) в соответствии с правилами закраски.
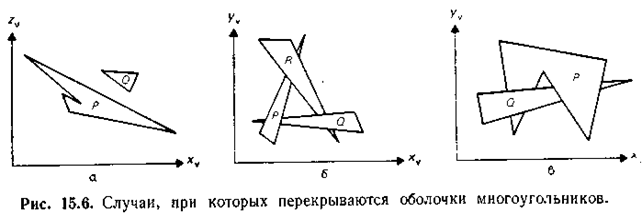
При сложных пересечениях многоугольников возможны неопределенности.
Алгоритм проверки: для простоты будем считать, что рассматривается параллельное проектирование вдоль оси Oz, грань Р находится в конце списка (самая удаленная). Перед выводом грани Р следует убедиться, что никакая другая грань Q, проекция которой на ось Oz пересекается с проекцией грани Р, не может закрываться гранью Р. И если это условие выполнено, то грань Р должна быть выведена раньше.
1. Пересекаются ли проекции этих граней на ось Ох? (PXmax<QXmin) or (PXmin>QXmax). X-оболочки не перекрываются, значит, многоугольники также не перекрываются.
2. Пересекаются ли их проекции на ось Оу? (PYmax<QYmin) or (PYmin>QYmax).
3. Находится ли грань Р по другую сторону от плоскости, проходящей через грань Q, чем начало координат (наблюдатель)? P целиком лежит со стороны от плоскости Q, которая дальше от точки зрения (наблюдения). 4. Находится ли грань Q по ту же сторону от плоскости, проходящей через грань Р, что и начало координат (наблюдатель)? Q лежит со стороны плоскости, содержащей P, которая ближе к точке наблюдения
Подзадача: с какой стороны от плоскости Q лежит точка (грань P)? Уравнение плоскости через три точки Q1, Q2, Q3 равно Ax+By+Cz+D=0, где A = (y2 ‑ y1)×(z3 ‑ z1) ‑ (y3 ‑ y1)×(z2 ‑ z1); B = (z2 ‑ z1)×(x3 ‑ x1) ‑ (z3 ‑ z1)×(x2 ‑ x1); C = (x2 ‑ x1)×(y3 ‑ y1) ‑ (x3 ‑ x1)×(y2 ‑ y1); D = ‑ Ax1 ‑ By1 ‑ Cz1. С какой стороны от плоскости находятся точки P1(x4,y4,z4), P2(x5,y5,z5)? Вычисляем в каждой точке f Т = Ax + By + Cz + D: fТ>0 – точка P лежит дальше от плоскости Q от точке наблюдения; fТ<0 – точка P лежит ближе от плоскости Q к точке наблюдения; fТ=0 – точка P лежит на плоскости Q.
5. Пересекаются ли проекции этих граней на картинной плоскости? Проекции P и Q на плоскости X0Y не пересекаются
Подзадача: с какой стороны от прямой лежит точка? Уравнение прямой через две точки
y = bx+d,тогда fТ = y–bx–d: fТ>0 – точка лежит выше, правее (дальше) от начала координат; fТ<0 – точка лежит ниже, левее (ближе) от начала координат; fТ=0 – точка лежит на прямой. Подзадача: пересекаются ли 2 ребра?
Подзадача: пересекаются ли 2 многоугольника? Каждое ребро одной грани сравнить с каждым ребром другой. Если найдены 2 пересекающихся ребра => многоугольники пересекаются.
Если хотя бы на один из этих вопросов получен отрицательный ответ, то считается что эти две грани (Р и Q) упорядочены верно и сравниваем Р со следующей гранью. В противном случае считаем, что эти грани необходимо поменять местами, для чего проверяются следующие тесты: 3'. Находится ли грань Q по другую сторону от плоскости, проходящей через грань Р, чем начало координат? 4'. Находится ли грань Р по ту же сторону от плоскости, проходящей через грань Q, что и начало координат?
В случае если ни один из этих тестов не позволяет с уверенностью решить, какую из этих двух граней нужно выводить раньше, то одна из них разбивается на две грани плоскостью, проходящей через другую грань. В этом случае вопрос об упорядочении оставшейся грани и частей разбитой грани легко решается.
2.2. Особенности алгоритмов, Тесная связь с растром экрана (изображением), т. к. рассматривается г. с. к., где координаты X, Y точки объекта соответствуют координатам X, Y пиксела экрана, координата Z точки объекта сохраняется для сравнения дальности.
Проецирующие лучи проходят только через пиксели, координаты вершин объектов должны быть только целочисленными (объект преобразован в г. с. к.). Осуществляется переход от центральной проекции к бесконечной (т. е. объект изменяется так, что при параллельной проекции он выглядел как при центральной).
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.01 с.) |

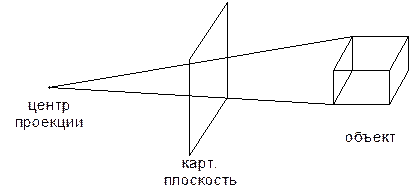

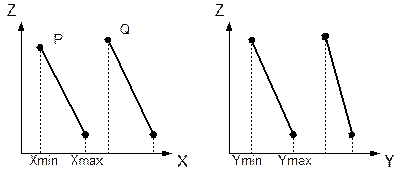 Предлагаются следующие 5 тестов в порядке возрастания сложности проверки:
Предлагаются следующие 5 тестов в порядке возрастания сложности проверки:
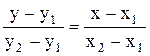 =>
=> 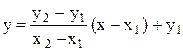 , где
, где 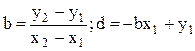 ;
;