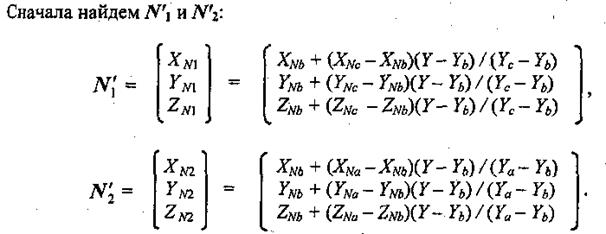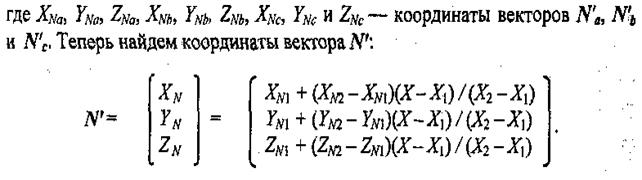Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм, использующий Z-буферСодержание книги Поиск на нашем сайте
Идея простейшего алгоритма. Буфер кадра хранит атрибуты (цвет) каждого пикселя экрана. Z-буфер (той же размерности) хранит значение глубины (Z-координаты) каждого пикселя в пространстве изображения. При развертке в растр новой грани для каждого нового пикселя сравнивается его глубина со значением из Z-буфера, если впереди (ближе) оказывается новый пиксель, то значение его глубины заносится в Z-буфер, а атрибут (цвет) ‑ в буфер кадра. При этом: 1) сцена может быть любой сложности;
Для работы алгоритма необходим большой объем памяти. Информацию о глубине нужно обрабатывать с большей точностью, чем координатную информацию на плоскости (х, у), обычно используют 20 бит. Буфер кадра размером 800´600´24 бит в комбинации с Z-буфером размером 800´600´20 бит требует почти 4 MБайта памяти (большинство оптимизаций видеоускоритлей связано с Z-буферами разных уровней детализации: 2х2, 4х4). Для ускорения вычисления z-координат при построчном разложении многоугольников в растр используется простая линейная зависимость:
отсюда следует, что .
Таким образом, вычисление z-координаты соседнего пиксела при растровой построчной развертке грани сводится к одной операции вычитания.
Алгоритм трассировки лучей
Общая идея: Есть источник, свет от источника падает на объект, поступает к наблюдателю (отразившийся от поверхности объекта). Однако не многие из лучей источника дойдут именно до наблюдателя. Сколько лучей надо учитывать?
Идея Аппеля: отслеживать (трассировать) луч в обратном направлении от наблюдателя к объекту через все точки растра. Упрощения: 1. Объект преобразован в с. к. изображения. 2. От центральной проекции переходим к параллельной (точка наблюдения стремится к бесконечности по z): - все лучи параллельны оси z; - каждый луч проходит через пиксель на экране до объекта.
Алгоритм Для каждого луча отслеживается, какие грани объекта имеют с ним пересечение, проверяется пересечение луча с каждой из граней, получается точка пересечения. Точки пересечения сортируются по глубине (по Z-координате). Точка пересечения с Zmin – видимая поверхность для данного пиксела. Атрибут этой точки грани и является характеристикой пиксела экрана.
1. Поиск точек пересечения с плоскостью грани. A = (y2 ‑ y1)×(z3 ‑ z1) ‑ (y3 ‑ y1)×(z2 ‑ z1); B = (z2 ‑ z1)×(x3 ‑ x1) ‑ (z3 ‑ z1)×(x2 ‑ x1); C = (x2 ‑ x1)×(y3 ‑ y1) ‑ (x3 ‑ x1)×(y2 ‑ y1);
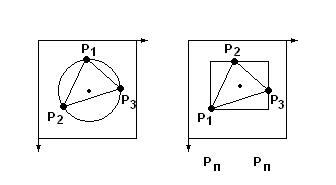
А) Вводят оболочку, с которой можно легко найти пересечение (окружность, прямоугольник). Окружность: центр О(x, y), R проходит через P1, P2, P3. Прямоугольник: Xmin, Xmax, Ymin, Ymax. Б) Определяем пересечение с оболочкой. Окружность: рассчитываем расстояние S от центра окружности О(Xo, Yo) до точки Pп(Xп, Yп). Если S≤R, то пересечение с оболочкой есть.
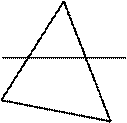
при выполнении всех этих условия точка пересечения трассирующего луча с гранью находится в прямоугольной оболочке грани. В) Если есть пересечение с оболочкой, определим, лежит ли точка
В формуле присутствует знак модуля. Знак выражения, стоящего Точка D лежит внутри треугольника ABC только тогда, когда все 3 треугольника ABD, BCD и CAD (именно с таким порядком вершин!) имеют одинаковую пространственную ориентацию. Считаем выражения для площадей этих треугольников (без модулей) и сравниваем их знаки. Если в описании граней единичного выпуклого замкнутого объекта все вершины перечислены в порядке, например, против часовой стрелки, то для определения видимости грани необходимо вычислить ее текущую ориентацию в г. с. к., и если она не совпадает с описанной (т. е. не против часовой стрелки), то грань не выводится (метод ориентации грани: лицевая/нелицевая). Этот метод очень прост, но не учитывает экранирование грани другой гранью объекта, а только ее ориентацию «к наблюдателю»/«от наблюдателя». Достоинства метода трассировки лучей: 1. Включает в себя растровую развертку. 2. Легко можно учитывать модель освещения (включая прозрачность, фактуру и т. д.). 3. Слабо зависит от числа граней в изображении. Недостатки: 1. Медленный поиск точки пересечения луча с гранью. 2. Быстродействие зависит от разрешения экрана. Модели освещения
Наиболее простым для моделирования источником является рассеянный естественный свет, т. к. он обеспечивает постоянное освещение всех поверхностей независимо от их ориентации. К сожалению, такой свет дает весьма нечеткие изображения, поскольку нередки ситуации, когда освещение обеспечивается только естественным светом. При естественном освещении две смежные стороны куба должны быть закрашены одинаково, а их общее ребро должно быть неразличимо. Более сложным (с точки зрения моделирования), но зато более реальным источником света является точечный источник, при использовании которого освещенность поверхности зависит от ее ориентации: если лучи направлены перпендикулярно к поверхности, она освещена ярко. Чем меньше угол падения лучей, тем меньше освещенность. Такое изменение освещенности позволяет эффективно распознавать трехмерную структуру объекта.
Зеркальное отражение света
Поверхность считается идеально зеркальной, если на ней отсутствуют какие-либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0,5 мкм.
Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны: чем больше длина волны, тем лучше отражение, так красные лучи отражаются сильнее, чем синие. При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов q, близких к 90 °. Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемых по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cos a)р, где a ‑ угол отклонения от линии идеально отраженного луча. Показатель р находится в диапазоне от 1 до 200 и зависит от качества полировки. Запишем это таким образом:
где I ‑ интенсивность излучения источника; КS ‑ коэффициент пропорциональности.
Диффузное отражение света
Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка, бумаги.
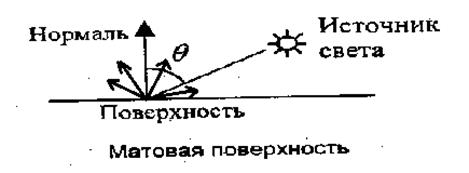
Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности:
где I ‑ интенсивность источника света; Kd ‑ коэффициент, который учитывает свойства материала поверхности. Значение Kd находится в диапазоне от 0 до 1. Интенсивность отраженного света не зависит от расположения наблюдателя.
Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света. При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент:
где константы Kd и KS определяют отражательные свойства материала. Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов q и a. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:
где Ia ‑ интенсивность рассеянного света; Кa ‑ константа. Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности; поэтому на практике часто реализуют модель, выражаемую эмпирической формулой:
где R ‑ расстояние от центра проекции до поверхности; k – условная константа. Как определить цвет закрашивания точек объектов в соответствии с данной моделью? Наиболее просто выполняется расчет в градациях серого цвета (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициенты Kа и Kd различны для разных компонент: они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент KS будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент RGB. Методы закраски Метод Гуро
Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны, и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можно замаскировать за счет увеличения количества граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней ‑ такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить количество граней, что приводит к существенному замедлению визуализации: чем больше граней, тем меньше скорость рисования объектов.
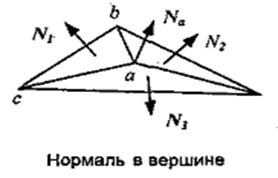
Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяций цветов примыкающих граней. Закрашивание граней по методу Гуро осуществляется в четыре этапа. 1. Вычисляются нормали к каждой грани ‑ вектор N(A,B,C), где A, B, C – коэффициенты уравнения плоскости грани Ax+By+Cz+D=0 (или методом векторного произведения двух ребер-векторов грани). 2. Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней, так вектор нормали в вершине а
3. На основе нормалей в вершинах Na, Nb, Nc вычисляются значения интенсивностей в вершинах Ia, Ib, Ic согласно выбранной модели отражения света 4. Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.
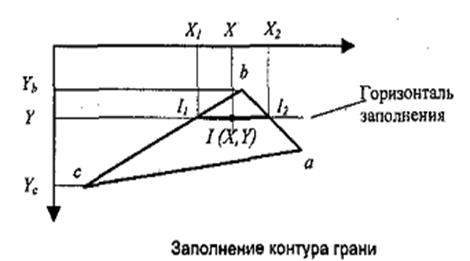
Определение интерполированных значений интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно выполнять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах.
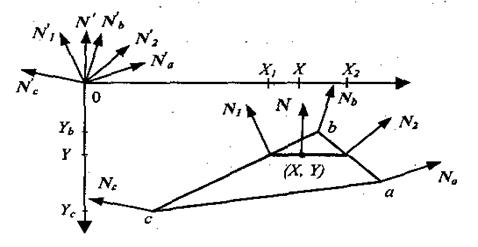
Метод Фонга Аналогичен методу Гуро, но при использовании метода Фонга для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей. 1. Определяются нормали к каждой грани ‑ вектор N(A,B,C) – или векторным произведением ребер-векторов. 2. По нормалям к граням определяются нормали в вершинах (Na, Nb, Nc) – усреднением по примыкающим граням. 3. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали N' – описано ниже. 4. По направлению векторов нормали N' определяется цвет I точек грани в соответствии с выбранной моделью отражения света – для диффузного отражения скалярное произведение векторов нормали и освещения. Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N'a, N'b, N'с, исходящими из центра координат плоскости проецирования и параллельными соответствующим нормалям Na, Nb, Nс в вершинах а, b и с.
Интерполяция векторов нормалей.
Вектор N' параллелен вектору N для нормали в точке (X, Y), поэтому его можно использовать для расчета отражения света так же, как и вектор нормали N.
Метод Фонга сложнее, чем метод Гуро. Для каждой точки (пиксела) поверхности необходимо выполнять намного больше вычислительных операций. Тем не менее он дает значительно лучшие результаты, в особенности при имитации зеркальных поверхностей и больших поверхностей, перпендикулярных наблюдателю. В настоящее время применяется только метод Фонга.
|
|||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.119 (0.014 с.) |

 2) элементы изображения (грани) могут заноситься в любой последовательности (не нужно сортировок и т. д.).
2) элементы изображения (грани) могут заноситься в любой последовательности (не нужно сортировок и т. д.).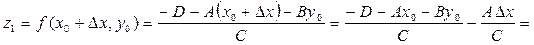
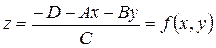
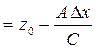 . Найдем z-координату для соседней точки:
. Найдем z-координату для соседней точки: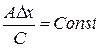
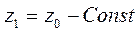
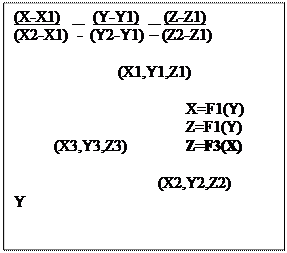 Основной недостаток алгоритма Z-буфера состоит в трудоемкости и высокой стоимости устранения лестничного эффекта, а также реализации эффектов прозрачности и просвечивания. Поскольку алгоритм заносит пикселы в буфер кадра в произвольном порядке, то нелегко получить информацию, необходимую для методов устранения лестничного эффекта, основывающихся на предварительной фильтрации. При реализации эффектов прозрачности и просвечивания, пикселы могут заноситься в буфер кадра в некорректном порядке, что ведет к локальным артефактам изображения.
Основной недостаток алгоритма Z-буфера состоит в трудоемкости и высокой стоимости устранения лестничного эффекта, а также реализации эффектов прозрачности и просвечивания. Поскольку алгоритм заносит пикселы в буфер кадра в произвольном порядке, то нелегко получить информацию, необходимую для методов устранения лестничного эффекта, основывающихся на предварительной фильтрации. При реализации эффектов прозрачности и просвечивания, пикселы могут заноситься в буфер кадра в некорректном порядке, что ведет к локальным артефактам изображения.

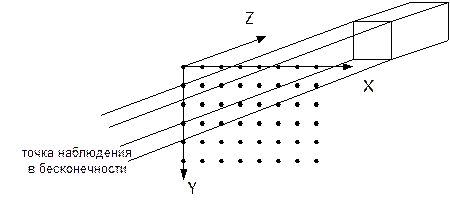
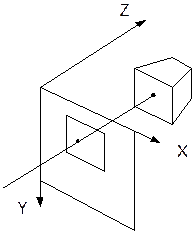 Основная задача: определить точку пересечения (требует 75 – 90 % времени), объект должен состоять из таких граней, для которых можно найти точку пересечения (треугольники, многоугольники). Выделяются подзадачи:
Основная задача: определить точку пересечения (требует 75 – 90 % времени), объект должен состоять из таких граней, для которых можно найти точку пересечения (треугольники, многоугольники). Выделяются подзадачи: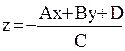 ,
,  D = ‑ Ax1 ‑ By1 ‑ Cz1.
D = ‑ Ax1 ‑ By1 ‑ Cz1.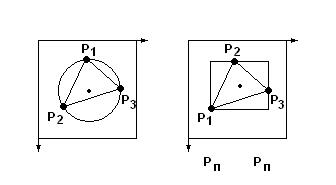 2. Определить, имеет ли грань пересечение с лучом.
2. Определить, имеет ли грань пересечение с лучом.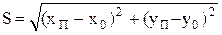
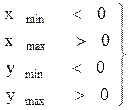 Прямоугольник: осуществляем перенос, при котором точка пересечения Pп становится началом координат (трассирующий луч становится осью Z):
Прямоугольник: осуществляем перенос, при котором точка пересечения Pп становится началом координат (трассирующий луч становится осью Z):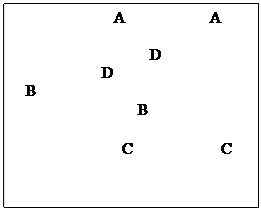 Площадь треугольника
Площадь треугольника 
 S = | x 1 × y 2 ‑ x 2 × y 1 + x 2 × y 3 ‑ x 3 × y 2 + x 3 × y 1 ‑ x 1 × y 3| / 2
S = | x 1 × y 2 ‑ x 2 × y 1 + x 2 × y 3 ‑ x 3 × y 2 + x 3 × y 1 ‑ x 1 × y 3| / 2


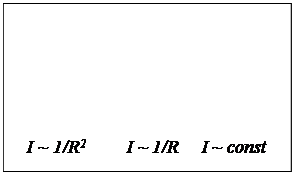 Внешний вид поверхности зависит от 1. вида источника света, которым освещается объект, от 2. свойств поверхности, а также от 3. положения и ориентации поверхности относительно источника света и других поверхностей. Источник света может представлять собой точечный источник, подобный Солнцу или лампе накаливания, или же распределенный источник, аналогичный группе ламп дневного света. На практике во многих ситуациях присутствует также естественный свет, падающий с самых различных направлений.
Внешний вид поверхности зависит от 1. вида источника света, которым освещается объект, от 2. свойств поверхности, а также от 3. положения и ориентации поверхности относительно источника света и других поверхностей. Источник света может представлять собой точечный источник, подобный Солнцу или лампе накаливания, или же распределенный источник, аналогичный группе ламп дневного света. На практике во многих ситуациях присутствует также естественный свет, падающий с самых различных направлений.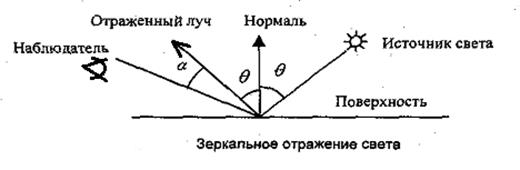

 Угол между нормалью и падающим лучом (q) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости.
Угол между нормалью и падающим лучом (q) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости.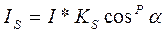 ,
,
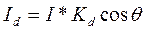 ,
,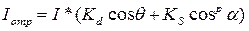 ,
,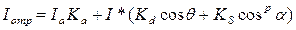 ,
,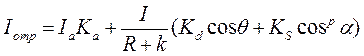 ,
,
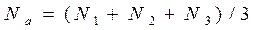 .
.