
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нестационарный режим движения жидкостиСодержание книги
Поиск на нашем сайте Рассмотрим задачу моделирования на примере простой гидравлической системы, рассмотренной выше (рис. 2.1.1). При построении динамических моделей конечные балансовые уравнения 6 и 7 в системе уравнений математического описания (9) превращаются в обыкновенные дифференциальные уравнения вида:
где Если эти емкости являются цилиндрическими, то объем жидкости в них определяется по формуле VR = S × H (17) (S – площадь поперечного сечения цилиндра), и вышеприведенные обыкновенные дифференциальные уравнения (15) и (16) принимают следующий вид (в нумерации системы (9) – это будут уравнения 6 и 7): 6 7 Для решения системы дифференциальных уравнений на компьютере, т. е. получения соответствующего частного решения, необходимо задать начальные условия вида в принятой выше нумерации системы (9) – это будут уравнения
При этом решается задача Коши, или задача с начальными условиями, и получаемые частные решения представляют собой функции H 1(t) и H 2(t), рассматриваемые в замкнутом интервале [ t (0), t (k)], которые являются приближениями истинных функций решения Более общее представление систем двух дифференциальных уравнений (18) и (19) имеет вид:
где В итоге, математическое описание динамики простой гидравлической системы (см. рис. 2.1.1) представляет собой ту же самую систему уравнений (9), в которой балансовые уравнения 6 и 7 заменены на дифференциальные уравнения (18) и (19); в систему также включены два начальных условия (18 ') и (19 ') для получения частного решения на компьютере (общее решение обыкновенных дифференциальных уравнений, как правило, получают аналитическими методами). Таким образом, необходимо решить систему уравнений (9), из которых два являются дифференциальными – (18) и (19) – с начальными условиями (18 ') и (19 '). Для решения дифференциальных уравнений (18) и (19) целесообразно представить их в конечно-разностной форме в следующем виде в нумерации системы (9) – это будут уравнения
Если интервал интегрирования равен [ t (0), t ( k )], то правые части дифференциальных уравнений 1 2 3 4 5
8 P 5 = P 7 + r gH 1; 9 10 P 6 = P 8 + r gH 2; 11 Так как при решении системы двух дифференциальных уравнений –(18) и (19) – необходимо определить функции H 1(t) и H 2(t) [ t (0), t ( k )], т. е. и
|
||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

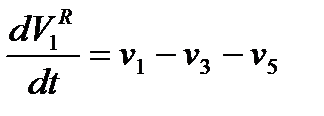 ; (15)
; (15) , (16)
, (16)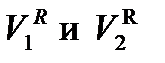 – объемы жидкости в верхней и нижней емкостях гидравлической системы, представленной на рис. 2.1.1.
– объемы жидкости в верхней и нижней емкостях гидравлической системы, представленной на рис. 2.1.1.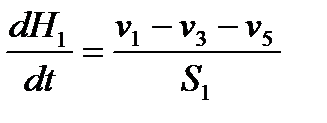 ; (18)
; (18)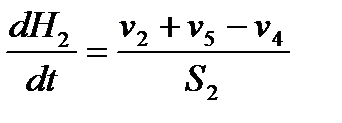 . (19)
. (19)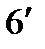 и
и 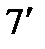 ):
):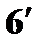
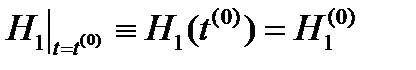 ; (18 ')
; (18 ')
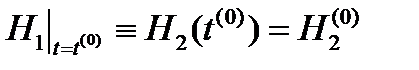 . (19 ')
. (19 ')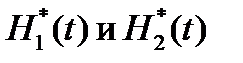 .
.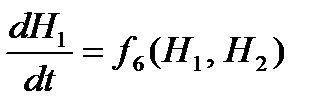 ; (20)
; (20)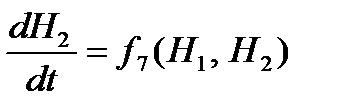 , (21)
, (21)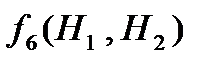 и
и 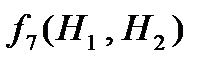 – правые части дифференциальных уравнений первого порядка, записанные в явном виде.
– правые части дифференциальных уравнений первого порядка, записанные в явном виде.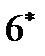 и
и  :
:
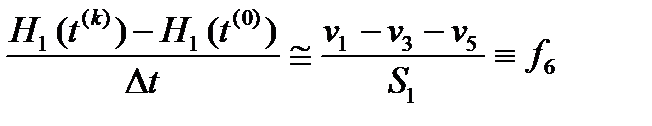 ; (18*)
; (18*)
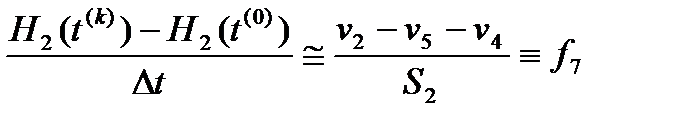 . (19*)
. (19*) и
и 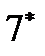 , а также, соответственно, (18*) и (19*), вычисляются при t (0), t (1), …, t ( k – 1). В результате конечно-разностных преобразований
, а также, соответственно, (18*) и (19*), вычисляются при t (0), t (1), …, t ( k – 1). В результате конечно-разностных преобразований 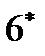 и
и 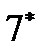 система уравнений (9) математического описания нестационарного режима гидравлической системы (рис. 2.1.1), представленная в конечно-разностной форме имеет вид:
система уравнений (9) математического описания нестационарного режима гидравлической системы (рис. 2.1.1), представленная в конечно-разностной форме имеет вид: = k 1 (P 1 – P 5)1/2;
= k 1 (P 1 – P 5)1/2;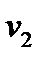 = k 2 (P 2 – P 6)1/2;
= k 2 (P 2 – P 6)1/2;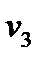 = k 3 (P 5 – P 3)1/2;
= k 3 (P 5 – P 3)1/2;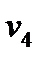 = k 4 (P 6 – P 4)1/2;
= k 4 (P 6 – P 4)1/2;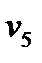 = k 5 (P 5 – P 6)1/2;
= k 5 (P 5 – P 6)1/2;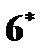
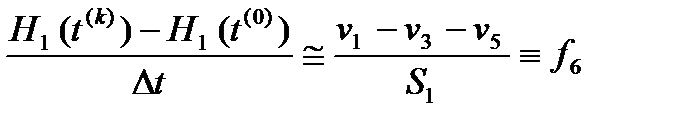 ;
;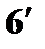
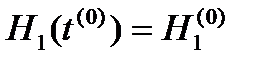 ; (22)
; (22)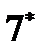
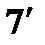
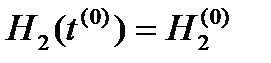 ;
;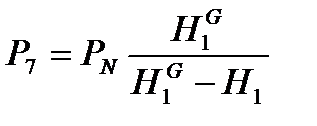 ;
;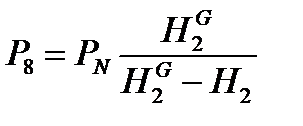 .
.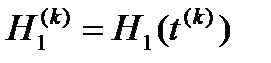 и
и 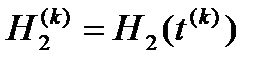 при заданных начальных условиях и
при заданных начальных условиях и 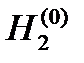 (18 ') и (19 '), то конечным результатом расчетов должны быть указанные функции, представленные в дискретном виде, при t = t (0), t (1), …, t ( k – 1), t ( k ). Последними значениями искомых функций являются определяемые на 12 и 13 шаге вычислений
(18 ') и (19 '), то конечным результатом расчетов должны быть указанные функции, представленные в дискретном виде, при t = t (0), t (1), …, t ( k – 1), t ( k ). Последними значениями искомых функций являются определяемые на 12 и 13 шаге вычислений 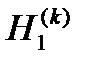 и
и 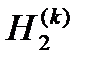 .
.


