
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое описание процессаСодержание книги
Поиск на нашем сайте Система независимых уравнений (9), приводимая ниже и описывающая поведение простой гидравлической системы в стационарном состоянии, состоит из следующих уравнений: а) определение скорости потоков жидкости через клапаны (3) – при программировании используется строгое уравнение (4): 1 2 3 4 5 б) расчета балансов (1) и (2): 6 7 с) Определение давлений жидкости (6) и газа (8) в закрытых емкостях: 8 P 5 = P 7 + r gH 1 ; 9 10 P 6 = P 8 + r gH 2 ; 11 Так как система конечных уравнений (9) включает 11 независимых уравнений(в дальнейшем используется последовательная нумерация уравнений от 1 до 11), она может быть решена, в принципе, относительно любых 11 переменных, которые называются определяемыми переменными. Все остальные переменные системы (9), соответствующие числу степеней свободы, должны задаваться. Кроме этого, должны быть специфицированы коэффициенты (например, коэффициенты пропускной способности клапанов – вектор Исходя из физических соображений, при гидравлическом расчете систем трубопроводов, представляющем собой решение системы 11 уравнений (9), определяемыми переменными выбираются: · расходы жидкости на всех участках · промежуточные давления в системе Р 5, Р 6, Р 7, Р 8 · уровни жидкости в двух ёмкостях Всего: 11 определяемых переменных. Давления на входе в систему P 1 и Р 2, а также давления на выходе из системы Р 3 и Р 4 задаются, и их число (в данном случае – 4) соответствует числу степеней свободы системы уравнений (9), которое определяется как разность между числом переменных и числом независимых уравнений. В рассматриваемом примере: 15 – 11 = 4. Эти четыре переменные могут задаваться независимо в соответствии с физическим смыслом решаемой задачи. Это означает, что если предполагается движение жидкости в соответствии со стрелками, изображенными на рис. 2.1.1, давления на входе в систему Р 1 и Р 2 должны быть больше давлений на выходе Р 3 и Р 4. Система 11 конечных уравнений (9), решаемая относительно следующих 11 определяемых переменных: v1, v2, v3, v4, v5, P5, P6, P7, P8, H1, H2 (10) является системой нелинейных уравнений. Для ее решения наиболее целесообразно использовать декомпозиционный метод, который позволяет существенно снизить размерность решаемой задачи и определять все искомые переменные путем решения системы (или систем) уравнений значительно меньшей размерности, чем размерность исходной системы. Размерность исходной системы уравнений (9) равна 11. Каждое уравнение системы (9) содержит несколько определяемых переменных: как минимум две. Начальные приближения для итерационных расчетов при решении нелинейных уравнений следует задавать в тех уравнениях, которые содержат наименьшее число определяемых переменных (в данном случае две) и могут быть хорошо обоснованы из физических соображений. Например, значение приближения Н 1 может быть задано в интервале [0, Первым шагом вычислительной процедуры будет определение переменной Р 7 в уравнении 9. Заданное значение приближения Таким образом, определение корректного значения Н 1 приведет соответственно к получению корректных значений и Р 7, Р 5, v 1, v 3, v 5, P 6, v 2, v 4, т. е. 9 из 11 искомых переменных. Для коррекции Н 1 должно использоваться уравнение 7, в котором все переменные известны из предыдущих расчетов – шаг 9. Когда система уравнений математического описания решена, то уравнение 7 вида: v 2{ H 1} + v 5{ H 1} – v 4{ H 1} = 0 (11) должно превратиться в равенство. Переменная Н 1 в фигурных скобах в этом случае означает, что каждое слагаемое этого уравнения зависит от переменной Н 1, и оно должно быть решено относительно Н 1 для получения ее корректного значения. Реализацию алгоритма решения уравнения 7 можно рассматривать как процедуру коррекции переменной Н 1 и, соответственно, определение значений переменных Р 7, P 5, v 1, v 3, v 5, P 6, v 2 и v 4. Наиболее эффективным алгоритмом для коррекции переменной Н 1 и решения уравнения 7 является метод половинного деления, с нижней границей интервала поиска – 0 и верхней границей При решении уравнения 7 в итерационном цикле на шаге 6 необходимо определить Р 6 из уравнения 5. Так как на предыдущих этапах расчетов v 5 может получиться как положительным, так и отрицательным, выражение для определения Р 6 должно учитывать это обстоятельство – используется функция знака sgn(x) (5) для решения уравнения 5:
Для определения двух оставшихся переменных Р 8 и Н 2 в уравнение 10 подставляется Р 8 из уравнения 11 системы уравнений математического описания (9). В результате получается квадратное уравнение относительно Н 2 (Р 6 известно из предыдущих расчетов):
Наконец, для определения значения Н 2 используется алгоритм вычисления корней квадратного уравнения и выбирается тот из корней, который располагается в интервале [0,
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 = k 1 (P 1 – P 5)1/2;
= k 1 (P 1 – P 5)1/2;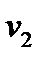 = k 2 (P 2 – P 6)1/2;
= k 2 (P 2 – P 6)1/2;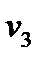 = k 3 (P 5 – P 3)1/2 ;
= k 3 (P 5 – P 3)1/2 ; 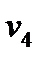 = k 4 (P 6 – P 4)1/2;
= k 4 (P 6 – P 4)1/2;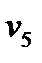 = k 5 (P 5 – P 6)1/2.
= k 5 (P 5 – P 6)1/2.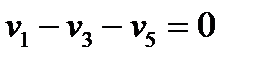 ; (9)
; (9)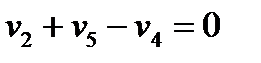 .
.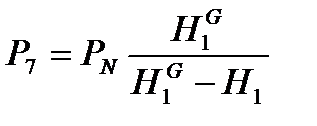 ;
;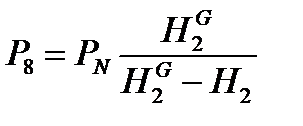 .
.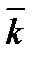 ), а также постоянные в системе уравнений (9) – геометрические высоты емкостей
), а также постоянные в системе уравнений (9) – геометрические высоты емкостей 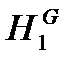 ,
, 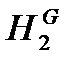 , давление в незаполненной жидкостью емкости PN и плотность жидкости r.
, давление в незаполненной жидкостью емкости PN и плотность жидкости r.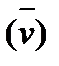 : 5 определяемых переменных;
: 5 определяемых переменных;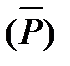 : 4 определяемых переменных;
: 4 определяемых переменных;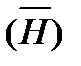 : 2 определяемые переменные.
: 2 определяемые переменные.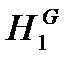 ], так как высота емкости
], так как высота емкости 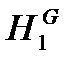 задана в условии задачи.
задана в условии задачи.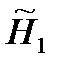 и найденная переменная Р 7 справедливы для всей системы уравнений и поэтому эти величины должны использоваться и другими уравнениями системы. В уравнении 8 теперь известны Н 1 и Р 7, что позволяет решить это уравнение относительно Р 5 на шаге 2 вычислительной процедуры. Дальнейшие последовательные шаги расчетов дают возможность определить только приближенные значения v 1, v 3, v 5, P 6, v 2, v 4, что связано с выбором в самом начале реализуемой процедуры вычисления приближения величины
и найденная переменная Р 7 справедливы для всей системы уравнений и поэтому эти величины должны использоваться и другими уравнениями системы. В уравнении 8 теперь известны Н 1 и Р 7, что позволяет решить это уравнение относительно Р 5 на шаге 2 вычислительной процедуры. Дальнейшие последовательные шаги расчетов дают возможность определить только приближенные значения v 1, v 3, v 5, P 6, v 2, v 4, что связано с выбором в самом начале реализуемой процедуры вычисления приближения величины 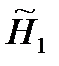 .
.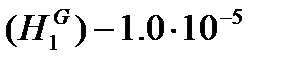 , так как только в этом случае знаменатель уравнения 9 системы уравнений математического описания (9) не станет равным нулю при подстановке в него верхней границы
, так как только в этом случае знаменатель уравнения 9 системы уравнений математического описания (9) не станет равным нулю при подстановке в него верхней границы 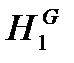 .
.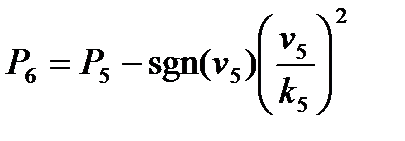 . (12)
. (12)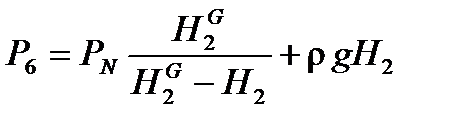 . (13)
. (13)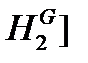 .
.


