
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод взвешенного подвижного (скользящего) среднего (weighted moving average).Содержание книги
Поиск на нашем сайте
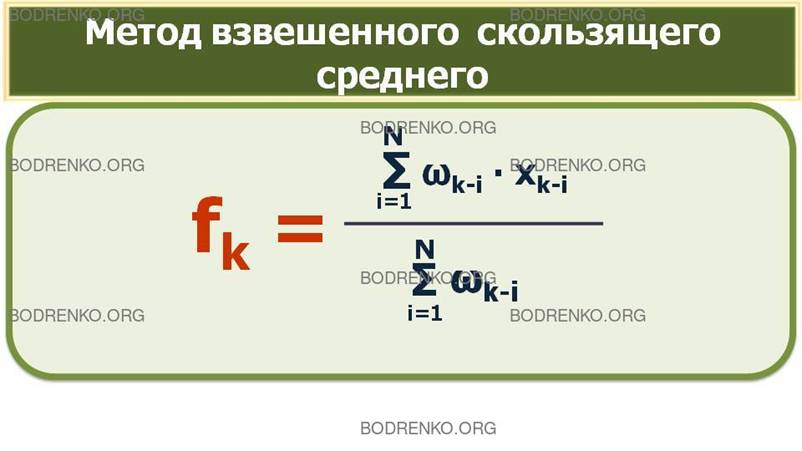
При составлении прогноза методом усреднения часто приходится наблюдать, что влияние используемых при расчете реальных показателей оказывается неодинаковым, при этом обычно более свежие данные имеют больший вес. Математически метод взвешенного подвижного среднего можно описать формулой:
где xk-i — реальное значение показателя в момент времени tk-i, N — число предшествующих моментов времени, используемых при расчете; fk — прогноз на момент времени tk. ωk-i — вес, с которым используется показатель xk-i при расчете.
ЗАМЕЧАНИЕ. Вес — это всегда положительное число. В случае, когда все веса одинаковы, мы получаем формулу (1). Для расчетов обратимся к исходному временному ряду, считая, что при составлении прогноза на завтрашний день объем сегодняшних продаж мы возьмем с весом 60, вчерашних — с весом 30, а позавчерашних - с весом 10: ω3 = 60, ω2 = 30, ω1 = 10. Мы имеем:
На рисунке 13 дается графическое представление проведенных расчетов: сплошными линиями соединены реальные значения, а пунктирными — прогнозируемые.
-
- 4 - - 2 - -
1 2 3 4 5 6 7 8
Рис. 13. Сравнение реальных и прогнозируемых показателей.
Для стационарных рядов существует система весовых множителей, позволяющая обеспечить минимальную ошибку прогноза. Эти множители определяются видом автоковариационной функции. Известен метод вычисления таких оптимальных весовых функций для постоянного уровня, тренда и сезонных коэффициентов. В каждом из этих случаев весовые множители экспоненциально уменьшаются по закону αj, а различные значения α, получаемые для уровня, тренда и сезонных коэффициентов, определяются систематическими исследованиями точности прогнозов, получаемых при различных комбинациях весовых функций. Во многих случаях целесообразно использовать последовательность ωj = αj, 0 < α <1, придающую более высокий вес более поздней информации и позволяющую относительно просто оценивать значения коэффициентов даже достаточно сложных моделей, таких, в которых для описания сезонных циклов используются полиномы в сочетании с преобразованиями Фурье (подобное представление можно рассматривать как сложные полиномы).
Для модели экспоненциально взвешенного скользящего среднего предложены способы, с помощью которых в те периоды времени, когда средняя ошибка прогноза близка к нулю (благодаря правильности модели и ее коэффициентов), скорость затухания α может быть увеличена; а в те периоды времени, когда средняя ошибка прогноза существенно отличается от нуля и существует опасность того, что модель может «забыть» старую информацию (в этом случае требуется уточнение прогноза), скорость затухания α может быть уменьшена.
Уточнение прогноза производится по принципу обратной связи — новые прогнозы корректируются на основе учета ошибок в предшествующих прогнозах. Если при выборе весовых множителей в процессе составления прогноза также используется обратная связь, то не только строгий анализ областей устойчивости данной системы, но и любой анализ вообще становится фактически невозможным. Для анализа эффективности какого-либо метода недостаточно привести примеры, подтверждающие его полезность. Необходимо также выявить области (если они существуют), в которых применение рассматриваемого метода невозможно или неэффективно.
|
|||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.164 (0.006 с.) |

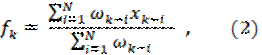
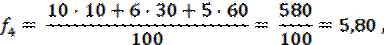
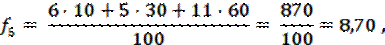
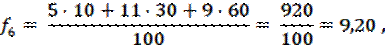
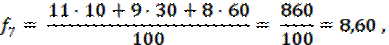
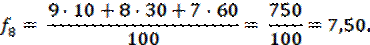


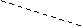
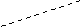

 10 -
10 -
 -
-

 8 -
8 - 6 -
6 -



