
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения прямой, проходящей через точку параллельно вектору (канонические уравнения прямой)Содержание книги
Поиск на нашем сайте
называемые каноническими уравнениями прямой в пространстве. Уравнения прямой, проходящей через две данные точки Пусть прямая проходит через две точки:
уравнения прямой, проходящей через две данные точки.
Векторное уравнение прямой. Параметрические уравнения прямой Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки
Так как векторы
Полученные уравнения называются параметрическими уравнениями прямой. При изменении параметра Замечание. Если принять каждую из равных дробей в канонических уравнениях прямой Уравнение прямой с угловым коэффициентом. Пусть дана прямая L на координатной плоскости Оху. Определение. Углом наклона прямой к оси абсцисс называется угол поворота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.
рис.1. Из определения следует, что угол наклона Пусть
– общее уравнение прямой L, где
Уравнение прямой L принимает вид:
Определение. Уравнение прямой вида
называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.
|
||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.26 (0.005 с.) |

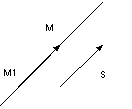
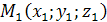 параллельно вектору
параллельно вектору 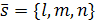 . Так как любой ненулевой вектор, параллельный данной прямой, является ее направляющим вектором, то для любой точки
. Так как любой ненулевой вектор, параллельный данной прямой, является ее направляющим вектором, то для любой точки 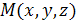 , лежащей на данной прямой, вектор
, лежащей на данной прямой, вектор 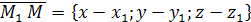 коллинеарен направляющему вектору
коллинеарен направляющему вектору 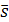 . Поэтому их соответствующие координаты должны быть пропорциональны, следовательно, имеют место равенства:
. Поэтому их соответствующие координаты должны быть пропорциональны, следовательно, имеют место равенства:
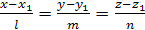 ,
,
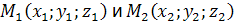 ,
, 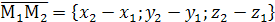 , и уравнения
, и уравнения 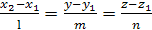 принимают вид:
принимают вид: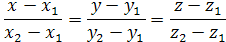
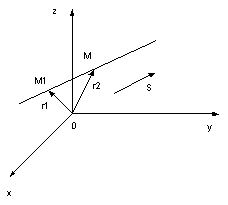
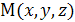 на прямой. Очевидно, что
на прямой. Очевидно, что 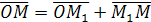 .
Так как векторы
.
Так как векторы 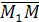 и
и 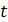 , что
, что 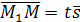 , причем число
, причем число 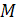 на прямой. Множитель
на прямой. Множитель 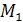 и
и 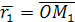 и
и 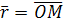 , получаем
, получаем 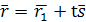 . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра
. Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра 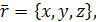
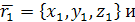
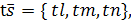 то
то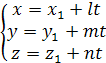 .
.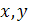 и
и 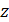 и точка
и точка 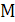 перемещается по прямой.
перемещается по прямой.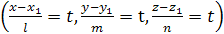 , то можно получить параметрические уравнения
, то можно получить параметрические уравнения 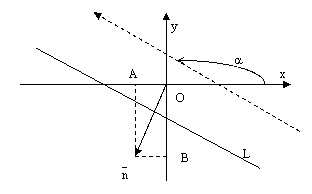
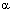 прямой L к оси Ох может изменяться от нуля до
прямой L к оси Ох может изменяться от нуля до 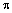 :
: 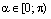 . Если прямая
. Если прямая 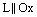 , то
, то 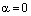 .
.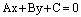 (1)
(1)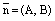 – нормальный вектор прямой L и
– нормальный вектор прямой L и 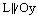 . Тогда
. Тогда 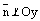 и
и 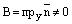 (см. рис.1). Выразим у из уравнения (1)
(см. рис.1). Выразим у из уравнения (1)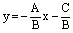 .
.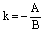 ,
, 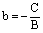 .
.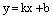 .
.


