
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение конструктивных элементов конического колесаСодержание книги
Поиск на нашем сайте Размеры колеса, полученные ранее: d ae 2; Re; me, b. Посадочный диаметр, мм:
где [t] = 25 МПа – допускаемое касательное напряжение. Полученное значение посадочного диаметра округлить до ближайшего большего значения из ряда нормальных линейных размеров. Толщина обода, мм: Ширина обода, мм: Наружный диаметр ступицы, мм: Длина ступицы, мм: Толщина диска, мм: Радиусы закруглений R ≥1 мм Размер а принимается равным 1…2 мм. Размер K принимается конструктивно. Фаску на торцах зубьев выполняют параллельно оси отверстия колеса размером
4.4. Разработка рабочего чертежа конического зубчатого колеса На чертеже конического колеса ставят следующие осевые размеры (рис. 4.2): Ц1 – цепочный, определяющий положение вершины делительного конуса колеса; Ц2 – цепочный, определяющий величину осевого зазора в комплекте вала с подшипниками; b – ширина зубчатого венца; а1 – размер, координирующий положение венца относительно ступицы; а2, а3 – размеры углублений; а4 – размер, координирующий осевое положение зуба относительно ступицы колеса; Г – габаритный размер. Кроме осевых размеров на чертеже конического колеса приводят следующие размеры зубчатого венца: внешние диаметры
Звёздочкой обозначают размеры для справок. Допуски формы и взаимного расположения поверхностей конических зубчатых колёс определяют так же, как и для цилиндрических. Таблица параметров для конических зубчатых колёс по форме и размерам такая же, как и для цилиндрических. Пример заполненной таблицы приведен в правом верхнем углу рабочего чертежа конического колеса (рис. 4.8). В первой части таблицы приводят: - внешний модуль me для прямозубого колеса; - средний нормальный модуль mn для колёс с круговыми зубьями; - число зубьев z; - тип зуба: «Прямой», «Круговой»; - осевую форму зуба (I, II, или III) по ГОСТ 19325-73 для колёс с прямыми зубьями; - средний угол наклона зуба b n для колёс с круговыми зубьями; - направление линии зуба (правое, левое) для колёс с круговыми зубьями; - исходный контур по ГОСТ 13754-81 для колёс с прямыми зубьями; - исходный контур по ГОСТ 16202-81 для колёс с круговыми зубьями; - коэффициент смещения с соответствующим знаком: внешний окружной xe для колёс с прямыми зубьями, средний нормальный xn для колёс с круговыми зубьями (при отсутствии смещения в графе проставляют 0); - коэффициент изменения толщины зуба x t с соответствующим знаком (при отсутствии изменения расчётной толщины в графе проставляют 0); - угол делительного конуса d; - номинальный диаметр d 0 зуборезной головки для зубчатого колеса с круговыми зубьями; - степень точности, вид сопряжения и обозначение стандарта на нормы точности по ГОСТ 1758-81. Вторую часть таблицы – одну - две строки оставляют свободной. В третьей части таблицы приводят: - межосевой угол передачи S; - средний модуль mm для колеса с прямыми зубьями; - внешний окружной модуль mte для колеса с круговыми зубьями; - внешнее и среднее конусные расстояния; - средний делительный диаметр d; - угол конуса впадин d I; - внешнюю высоту he зуба; - обозначение чертежа сопряженного колеса.
4.5. Пример выполнения расчетно-проектного задания Расчет конической передачи Исходные данные: Крутящий момент на валу конического колеса Т 3 = 35924 Н×мм. Число оборотов промежуточного вала редуктора n 3 = 464 об/мин. Передаточное число конической передачи u к = 3,15. Срок службы привода Lh = 29784 часов. Выбор материалов для изготовления конической зубчатой передачи: - шестерня – Сталь 45, термообработка - улучшение до твёрдости 235…260 НВ; - колесо – Сталь 45, термообработка - нормализация до твёрдости 180…205 НВ. Допускаемые контактные напряжения определяем по материалу колеса, как менее твёрдого.
где
N0 = 107 – базовое число циклов нагружения;
SH = 1,1 – коэффициент безопасности.
Допускаемые напряжения изгиба:
где σ F 01, σF 02 – предел выносливости материала по напряжениям изгиба при отнулевом цикле нагружения для шестерни и колеса, соответственно;
N F 0 = 5∙106 – базовое число циклов, т.к. N 2 > N F 0, то SF = 1,75 – коэффициент безопасности.
Определение внешнего делительного диаметра колеса de, мм:
где KH b –коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, с прирабатывающимисяпрямыми зубьями KH b= 1; u Z – коэффициент, учитывающий вид зубьев конических колёс, для прямозубых колёс u Z=1.
Принимаем Определяем углы делительных конусов шестерни d1 и колеса d2:
Определяем внешнее конусное расстояния Re, мм:
Определение ширины зубчатого венца b, мм:
где y R = 0,285 – коэффициент ширины зубчатого венца.
Определяем внешний окружной модуль зацепления, мм:
Назначаем mе=2,5 мм. Определяем числа зубьев. Число зубьев колеса: Число зубьев шестерни: Фактическое передаточное число:
Отклонение фактического передаточного числа от номинальной величины:
Определяем действительные углы делительных конусов шестерни d1 и колеса d2:
Геометрические параметры зацепления, мм: делительный диаметр шестерни диаметры окружностей выступов: шестерни колеса диаметры окружностей впадин: шестерни колеса Определим средний окружной модуль, мм:
Определяем средние делительные диаметры шестерни dm1 и колеса dm2, мм:
Проверочный расчёт. Определяем окружную скорость, м/c:
По окружной скорости назначаем 8-ю степень точности передачи. Определяем коэффициенты расчётной нагрузки. Коэффициенты KF a и KH a, учитывающие распределение нагрузки между зубьями, для прямозубой передачи принимаем: KF a= KH a= 1. По степени точности и окружной скорости по таблице 3.6 определяем коэффициенты динамической нагрузки при расчете по контактным напряжениям KHv= 1,128 и напряжениям изгиба KFv= 1,308. Коэффициенты KF b и KH b, учитывающие неравномерность распределения нагрузки по длине зуба, для прямозубой передачи принимаем: KH b= KF b = 1.
Окружная сила, действующая в зацеплении, Н:
Проверка по контактным напряжениям s H, МПа:
Определяем эквивалентные числа зубьев шестерни и колеса:
Коэффициент формы зуба шестерни YF1= 4,07и колеса - YF2= 3,63. Проверка прочности зубьев колеса и зубьев шестерни по напряжениям изгиба. Условия прочности:
где Y b= 1 - коэффициент, учитывающий наклон зубьев; u F – коэффициент, учитывающий вид зубьев конических колёс, для прямозубых колёс u F= 0,85.
Прочность зубьев по напряжениям изгиба обеспечена.
Определение конструктивных элементов конического колеса. Размеры колеса, полученные ранее, мм: d ae 2 =161,49; Re =83,94; me =2,5 b =24. Посадочный диаметр, мм:
где [ t ]= 25 МПа – допускаемое касательное напряжение. Толщина обода, мм: Ширина обода, мм: Наружный диаметр ступицы, мм: Длина ступицы, мм: Принимаем Толщина диска, мм: Принимаем толщину диска Радиусы закруглений принимаем R =1 мм Принимаем размеры: а = 2 мм и K =4 мм. Размер фаски
|
||||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 ,
, .
. .
.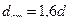 .
.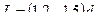 .
. .
. .
.
 и
и  ; угол dа конуса вершин зубьев; угол делительного конуса; угол
; угол dа конуса вершин зубьев; угол делительного конуса; угол  внешнего делительного конуса.
внешнего делительного конуса.
 ,
,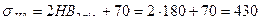 МПа, предел выносливости материала по контактным напряжениям при отнулевом цикле нагружения;
МПа, предел выносливости материала по контактным напряжениям при отнулевом цикле нагружения; - коэффициент долговечности при расчёте по контактным напряжениям;
- коэффициент долговечности при расчёте по контактным напряжениям;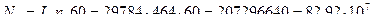 - расчётное число циклов нагружения зубьев колеса. Так как N 2 > N Н 0, то принимаем К HL = 1;
- расчётное число циклов нагружения зубьев колеса. Так как N 2 > N Н 0, то принимаем К HL = 1; МПа.
МПа. ,
, МПа;
МПа;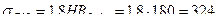 МПа.
МПа.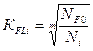 - коэффициент долговечности при расчёте по напряжениям изгиба.
- коэффициент долговечности при расчёте по напряжениям изгиба. .
. МПа,
МПа, МПа.
МПа. ,
, мм.
мм.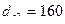 мм.
мм. ,
, .
.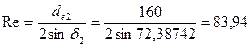 .
.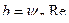 ,
,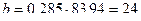 мм.
мм.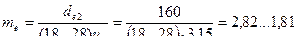 .
.
 .
.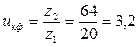 .
. .
. ,
, .
. ;
; ,
,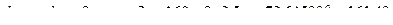 ;
;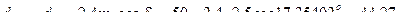 ,
, .
.
 ,
, .
. .
. ,
, .
. .
. .
.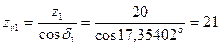 ,
,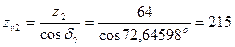 .
. ,
, ,
, ,
, .
.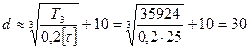 ,
, .
. .
. .
. .
. мм.
мм. .
. мм.
мм. мм.
мм.


