
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика методів вирішення задач оптимізації
Методи вирішення задач оптимізації поділяються на дві групи: Аналітичні методи - використовуються в тому випадку, коли цільова функція має аналітичний вираз, може бути диференцюєма в усьому діапазоні дослідження, при цьому число змінних повинно бути невеликим. Методи математичного програмування, які в свою чергу поділяються на три типи: а) Динамічне програмування - використовується для вирішення задач оптимізації багатостадійних процесів. Даний метод передбачає розділення процесу на стадії, оптимізація проводиться в два етапи. На першому етапі, починаючи з останньої стадії і рухаючись до початку, визначають оптимальні рівняння. На другому етапі, рухаючись від початку до кінця, визначають параметри; б) Лінійне програмування - це методи вирішення задач оптимізації з лінійними обмеженнями на область зміни змінних. При вирішенні таких задач зазвичай застосовують ітераційні процедури; в) Нелінійне програмування - ці методи використовуються в тому випадку, коли критерій оптимальності і обмеження мають нелінійний вид. Всі методи нелінійного програмування представляють собою чисельні методи пошукового типу. Суть їх в визначенні набору незалежних змінних, які забезпечують найбільший приріст цільової функції. Методи нелінійного програмування бувають: Методи випадкового пошуку - головна мета їх полягає в тому, що перебором випадкових сукупностей значень незалежних змінних відшукується оптимум цільової функції чи направлення руху до нього; Безградієнтні методи - вони використовують інформацію, отриману в процесі пошуку від порівняння значень цільової функції при виконанні чергового кроку пошуку. Безградієнтні методи можуть реалізувати як одномірний пошук, так і багатомірний. До методів багатомірних пошуків відносять метод покоординатного пошуку чи метод Гаусса-Зейделя, який засновано на почерговій зміні всіх незалежних змінних так, щоб по кожній з них досягалось екстремальне значення цільової функції; Градієнтні методи - в їх основі лежить аналіз похідної оптимальної функції, що передбачає аналіз лише безперервних та диференцюємих функцій. В даній курсовій роботі використовується метод «Крутого сходження» (метод Бокса-Уілсона), що запропоновано Дж. Боксом та К. Уілсоном як синтез кращих рис градієнтних методів і методу Гаусса-Зейделя, причому пробні досліди для з’ясування напрямку руху також виконують по особливому: методом ПФЕ.
Повним факторним експериментом (ПФЕ) - називається експеримент, що реалізує всі можливі неповторні комбінації рівнів незалежних управляючих факторів, кожен з яких варіюється на двох рівнях. Число цих комбінацій N = 2n визначає тип ПФЕ. Від градієнтних методів тут взято виконання робочого руху вздовж вектор-градієнту, визначеного в районі вихідної (базової) точки, а від методу Гаусса-Зейделя взято принцип руху не на один робочий крок (як в методі градієнту), а до досягнення екстремуму функції відклику в направленні градієнту, без коректування на кожному робочому кроці. Проведення подібних дослідів методом ПФЕ дозволяє більш точно оцінити направлення градієнту, ніж при традиційному методі градієнту. Дійсно, для оцінок На першому етапі методу Крутого сходження використовується наступна процедура: 1) Обирають основну (початкову) точку. Часто цю точку обирають в центрі області, яку слід дослідити; 2) Обирають інтервал варіювання ∆Xi, для кожного фактору Xi (і = 1, 2,..., n). Очевидно, що інтервал варіювання не повинен бути занадто малим, оскільки рух до екстремуму буде занадто повільним. Також він не повинен бути занадто великим, аби не вийти за межі області, що досліджується; 3) Визначають координати пробних точок для нижнього та верхнього рівнів варіювання факторів Xi за правилами ПФЕ:
Складають ортогональну матрицю планування ПФЕ, для чого фактори нормують за формулою:
4) За результатами ПФЕ розраховують оцінки коефіцієнтів нормованого рівняння регресії першого порядку:
Після визначення коефіцієнтів проводять статистичну перевірку значень
де
та прийнятому рівні значущості q; N - число точок факторного простору, в яких проводиться експеримент; m - число паралельних дослідів в цих точках. Також значущість коефіцієнтів можна визначити шляхом порівняння їх за абсолютним значенням. Якщо деякий коефіцієнт менший 5% від максимального, то їм можна знехтувати; ) Розраховують розрахункові і-ті складники робочих кроків в реальному масштабі:
максимальне по модулю з усіх ) Отримують практичні (наближені) і-ті складаючи робочих кроків Наближення проводиться за формулою:
до зручного значення чи з урахуванням похибок вимірювання по кожному фактору Xі. Знаки ) Розраховують координати всіх робочих точок (k = 1, 2,...) за напрямком градієнту в реальному масштабі:
в них послідовно виконують фіктивні та перевірочні (реальні) досліди. Розмір Фіктивні досліди полягають в отримані очікуваних (розрахункових) значень відклику Y за допомогою отриманого лінійного рівняння. Вони дозволяють: а) скоротити об’єм різних дослідів, тобто підвищують швидкість руху до екстремуму; б) мати уявлення, наскільки добре рівняння (9.1) апроксимує реальну верхню поверхню відклику, тобто наскільки розраховані значення Yk від результатів спостережуваних значень Yсп в реальних дослідах; в) оцінювати правильність вибору розміру складників практичного робочого кроку ( Реальні (перевірочні) досліди на початку руху з базової точки вздовж направлення градієнту ставлять через 2-4 фіктивні досліди, а при зменшенні приросту спостережуваних значень відклику у кожному наступному досліді у порівнянні з попереднім у робочих точках перевірочні досліди ставлять частіше, поблизу ж частного екстремуму виконують при кожному кроці. Робочий рух продовжують допоки не буде досягнутий частини екстремум за напрямком градієнту. Ознакою досягнення частного екстремуму є зменшення відклику в наступних перевірочних дослідах; ) Точку часного екстремуму на початковому направленні градієнту приймаємо за нову нульову точку і організуємо другий цикл Крутого сходження. Порядок роботи на другому етапі такий самий як і на першому. Різниця полягає в тому, що інтервал варіювання при постановці пробних дослідів ПФЕ і розмір робочих кроків у зв’язку з наближенням до екстремуму і збільшені кривизни поверхні відклику зазвичай обирають меншим, ніж на першому циклі. У випадку потреби проводять третій цикл Крутого сходження;
) Пошукові робочі рухи припиняють при досягненні області екстремуму. Ознакою досягнення екстремуму є статична не значимість оцінок аі коефіцієнтів при числах першого порядку, розрахованих за результатами ПФЕ навколо наступної нульової точки. Переваги методу «Крутого сходження»: а) висока перешкодозахищеність (перешкодостійкість) у розумінні точності оцінювання складників градієнту: якщо в градієнтних методах кожна складова аі оцінюється лише за двома точками факторного простору, то в ПФЕ, який в методі Крутого сходження використовується для цієї мети, кожен коефіцієнт оцінюється за всіма N = 2n точками; б) висока ефективність у розумінні швидкості руху до екстремуму: у порівнянні з методом Гаусса-Зейделя, а у порівнянні з градієнтними - за рахунок виключення пробних дослідів на кожному робочому кроці і за рахунок фіктивних дослідів; в) пробні досліди, що виконуються методом ПФЕ, дозволяють отримувати про оцінку аі-e коефіцієнтів при взаємодіях факторів zize, що характеризують кривизну поверхні відклику: збільшення аі-e при зменшенні аі зазвичай характеризує наближення до екстремуму; г) ПФЕ з застосуванням паралельних дослідів дозволяє достатньо просто здійснювати надійну статистичну інтерпретацію результатів; д) метод найбільш ефективний з усіх відомих при пологих поверхнях відклику. Недоліком розглянутого методу є дещо більша, ніж у попередніх методах, складність планування пробних дослідів, що потребує одночасного варіювання одразу всіх факторів відносно базової точки і менша оперативність у порівнянні з симплексним методом в умовах об’єктів, що дрейфують [1].
|
|||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.174 (0.012 с.) |
 коефіцієнтів в методі градієнту і в методі Крутого сходження при числі факторів n = 2 кількість точок для пробних дослідів в обох методах дорівнює 4, тобто однаково. Але якщо кожну оцінку
коефіцієнтів в методі градієнту і в методі Крутого сходження при числі факторів n = 2 кількість точок для пробних дослідів в обох методах дорівнює 4, тобто однаково. Але якщо кожну оцінку  в методі градієнту отримують за результатами дослідів лише в двох пробних точках (при будь-якій кількості п факторів), то в методі Крутого сходження - за результатами дослідів в усіх чотирьох точках (в загальному випадку в усіх 2n чи 2n-p пробних точках). Проведення пробних дослідів методом ПФЕ дозволяє також отримувати інформацію про взаємодію факторів і досить просто здійснювати статистичну перевірку результатів розрахунків.
в методі градієнту отримують за результатами дослідів лише в двох пробних точках (при будь-якій кількості п факторів), то в методі Крутого сходження - за результатами дослідів в усіх чотирьох точках (в загальному випадку в усіх 2n чи 2n-p пробних точках). Проведення пробних дослідів методом ПФЕ дозволяє також отримувати інформацію про взаємодію факторів і досить просто здійснювати статистичну перевірку результатів розрахунків.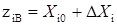 ; (9.1)
; (9.1)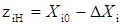 . (9.2)
. (9.2) . (9.3)
. (9.3) . (9.4)
. (9.4) . Для чого можна розрахувати критичне значення коефіцієнтів з використанням критерію Стьюдента:
. Для чого можна розрахувати критичне значення коефіцієнтів з використанням критерію Стьюдента: . (9.5)
. (9.5) - дисперсія оцінки коефіцієнту
- дисперсія оцінки коефіцієнту 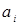 ;
; - обране з відповідних таблиць при числі ступенів свободи:
- обране з відповідних таблиць при числі ступенів свободи: ; (9.6)
; (9.6) ; (9.7)
; (9.7) , приймається за базове
, приймається за базове  ;
; . Для руху вздовж напрямку градієнту для чого наближують чи змінюють
. Для руху вздовж напрямку градієнту для чого наближують чи змінюють  до зручного
до зручного 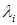 до
до  (9.8)
(9.8) ; (9.8)
; (9.8) зазвичай обирають так, аби перша робоча точка (k = 1) не виходила за межі області ПФЕ.
зазвичай обирають так, аби перша робоча точка (k = 1) не виходила за межі області ПФЕ. ), якщо за число кроків k = 3 досягається та перевищується максимально можливе розрахункове значення цільової функції (визначаємо з фізичних властивостей та обмежень, що існують для об’єкту), то
), якщо за число кроків k = 3 досягається та перевищується максимально можливе розрахункове значення цільової функції (визначаємо з фізичних властивостей та обмежень, що існують для об’єкту), то 


