
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система двох лінійних рівнянь з двома невідомими
Нехай маємо систему двох лінійних рівнянь з двома невідомими В даному пункті розглядатимемо лише такі системи. Розв ’ язком такої системи називається вектор
Система може не мати розв’язків, може мати єдиний розв’язок, або мати більше одного розв’язку. Приклади: 1). Дана система розв’язків не має. 2). Дана система має єдиний розв’язок 3). Дана система має безліч розв’язків Справді, Дві системи рівнянь називаються рівносильними (еквівалентними), якщо вони мають однакові множини розв’язків. Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок. Система рівнянь називається несумісною, якщо вона не має жодного розв’язку, тобто множина розв’язків є порожня множина Ø.
Матриця де Форму (2) запису системи (1) називають матричною. Крім такої форми запису, зручно використовувати запис у вигляді розширеної матриці: а також у векторній формі: де
Доведемо ряд важливих тверджень про розв’язки систем двох лінійних рівнянь з двома невідомими. Лема 1. Якщо матриця Доведення. Оскільки матриця Зрозуміло, що вектор Покажемо, що це єдиний розв’язок системи (1). Справді, нехай Лему доведено. Лема 2. Якщо матриця Доведення. 1). Нехай А – нуль-матриця, тоді Отже, 2). Нехай А – не є нуль-матрицею. Тому не всі
Зрозуміло, що
Оскільки не всі Лему доведено. Теорема. Система (1) має єдиний розв’язок тоді і тільки тоді, коли матриця цієї системи неособлива. Доведення. З леми 1 випливає, що якщо А неособлива, то система (1) має єдиний розв’язок. Навпаки. Нехай система (1) має єдиний розв’язок Справді, припустимо, що ненульовий вектор Отже, система (1) має принаймні два різні розв’язки. Суперечність. Отже, наше припущення хибне. Тому Теорему доведено. Наслідок. Система
|
|||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.67.251 (0.008 с.) |

 (1)
(1) , де
, де  – числа, для якого мають місце такі числові рівності:
– числа, для якого мають місце такі числові рівності:
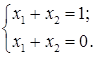
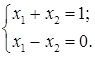

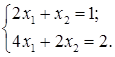
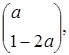 де
де  – довільне число.
– довільне число. і
і 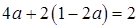 для довільного числа
для довільного числа  .
.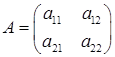 називається матрицею системи (1). Систему (1) зручно записувати в матричному вигляді
називається матрицею системи (1). Систему (1) зручно записувати в матричному вигляді (2)
(2)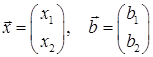 .
.


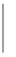
 , (3)
, (3) (4)
(4) – стовпці матриці
– стовпці матриці  .
. є неособливою, то система (1) має єдиний розв’язок.
є неособливою, то система (1) має єдиний розв’язок. є неособливою, то для неї існує обернена матриця
є неособливою, то для неї існує обернена матриця  .
. – розв’язок системи (1). Справді,
– розв’язок системи (1). Справді, 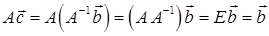 .
. - якийсь розв’язок системи (1). Тоді
- якийсь розв’язок системи (1). Тоді  . Тоді
. Тоді  , тобто
, тобто  . Це показує, що
. Це показує, що  .
. є особливою, то система
є особливою, то система  має ненульові розв’язки.
має ненульові розв’язки.
 - ненульовий роз’язок системи
- ненульовий роз’язок системи 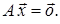
 дорівнюють нулю.
дорівнюють нулю.
 і
і
 має ненульові розв’язки.
має ненульові розв’язки. Покажемо, що тоді система
Покажемо, що тоді система  розв’язок
розв’язок  . Тоді
. Тоді  – розв’язок системи (1). Справді,
– розв’язок системи (1). Справді,  Зрозуміло, що
Зрозуміло, що  , бо
, бо 
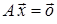 має лише один розв’язок. За лемою 2 А – неособлива матриця.
має лише один розв’язок. За лемою 2 А – неособлива матриця. ,
,  має лише нульовий розв’язок тоді і тільки тоді, коли
має лише нульовий розв’язок тоді і тільки тоді, коли  .
.


