
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трикутних матриць другого порядку
Будемо використовувати результати пункту 1.9. Нехай маємо матрицю виду Зведемо її до жорданової форми. Нехай Тоді Розглянемо наступні випадки: 1. Відповідно до твердження п. 1.9 нам потрібно знайти такі Оскільки Далі, Тоді Оскільки Отже,
тобто 2. Нехай Випадки: 2.1. Тоді матриця А вже має жорданову форму. 2.2.
Помножимо останнє рівняння на число Тоді Якщо ввести перепозначення:
Власні значення та власні вектори квадратної матриці другого порядку Число Ненульовий вектор
для деякого власного значення Рівність (1) еквівалентна рівності
де Теорема. Для того, щоб число Необхідність. Нехай
має ненульовий розв¢язок. Тому Достатність. Доведення достатності проводиться в зворотному порядку. Проведіть його самостійно! (Див. наслідок п. 2.1). Теорему доведено.
Рівняння
Отже, характеристичне рівняння можна записати і так
Для знаходження власних векторів матриці А потрібно розв¢язати систему
тобто для кожного власного значення Зауваження 1. Оскільки кожне квадратне рівняння має два комплексні розв¢язки, якщо врахувати їх кратність, то матриця А має або два різні, або два однакові власні значення. Тому матриця А завжди має власні вектори (тут враховуємо також Зауваження 2. Характеристичні рівняння подібних матриць однакові. Справді, нехай
|
|||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.16.184 (0.011 с.) |
 .
.


 і
і  , для яких
, для яких 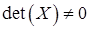 і матриця
і матриця  має жорданову форму. Для цього необхідно зробити
має жорданову форму. Для цього необхідно зробити  або
або  . Покажемо, що
. Покажемо, що  можна зробити рівним 0. Оскільки верхній рядок матриці А в такому разі змінювати не потрібно, то покладемо
можна зробити рівним 0. Оскільки верхній рядок матриці А в такому разі змінювати не потрібно, то покладемо  Нам потрібно знайти такий вектор
Нам потрібно знайти такий вектор  щоб
щоб 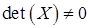 і
і 
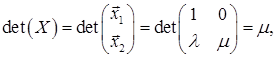 то
то 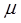 не повинно дорівнювати 0. Далі,
не повинно дорівнювати 0. Далі, 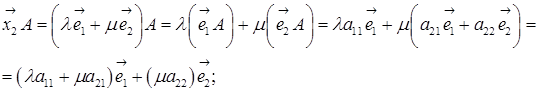
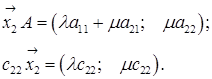

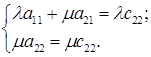
 , то з останнього рівняння системи маємо, що
, то з останнього рівняння системи маємо, що  Тоді з першого рівняння випливає
Тоді з першого рівняння випливає
 Оскільки
Оскільки  то можемо покласти
то можемо покласти  тоді
тоді  . Тому
. Тому  Отже, на підставі твердження п. 1.9
Отже, на підставі твердження п. 1.9  де С визначається з рівностей
де С визначається з рівностей
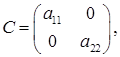 а
а  .
.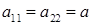 .
. .
. . Тоді
. Тоді 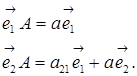
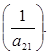

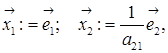 то
то 
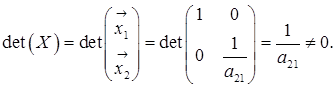 На підставі твердження п 1.9 матимемо, що
На підставі твердження п 1.9 матимемо, що  де
де 
 (комплексне) називається власним числом квадратної матриці
(комплексне) називається власним числом квадратної матриці  , якщо існує такий ненульовий вектор-рядок
, якщо існує такий ненульовий вектор-рядок 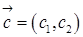 , що
, що . (1)
. (1) називається власним вектором матриці А, якщо
називається власним вектором матриці А, якщо
 матриці А.
матриці А. 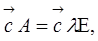 де
де 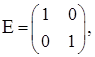 яка еквівалентна такій рівності
яка еквівалентна такій рівності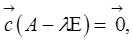
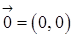 .
.
 - власне значення, тоді
- власне значення, тоді 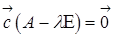 для деякого власного вектора
для деякого власного вектора  , тобто
, тобто 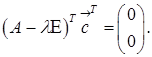 Оскільки
Оскільки  то це означає, що система
то це означає, що система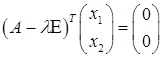
 Оскільки визначник при транспонуванні не змінюється, то
Оскільки визначник при транспонуванні не змінюється, то 
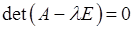 відносно невідомого
відносно невідомого  називається характеристичним рівнянням матриці А. З нього знаходимо власні значення. Зрозуміло, що
називається характеристичним рівнянням матриці А. З нього знаходимо власні значення. Зрозуміло, що

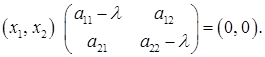


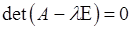 для власного значення
для власного значення 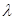 ).
).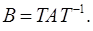 Тоді
Тоді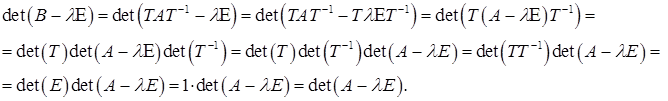 Приклад. Нехай
Приклад. Нехай  Тоді
Тоді  – характеристичне рівняння. Зрозуміло, що
– характеристичне рівняння. Зрозуміло, що  – множина усіх власних значень матриці А.
– множина усіх власних значень матриці А.


