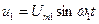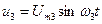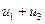Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведенияСодержание книги
Поиск на нашем сайте
Негармонические сигналы изменяются не по закону синуса или косинуса, а по более сложным законам. Математически такие сигналы описываются рядом Фурье. Негармонический сигнал можно получить: 1) При использовании источника негармонических колебаний 2) При наличии в цепи нелинейного элемента 3) При сложении нескольких сигналов гармонической формы Теорема Фурье: любой непрерывный сигнал можно представить в виде суммы отдельных гармонических функций кратных частот. Ряд Фурье с начальными фазами:
Спектральная диаграмма – это график зависимости амплитуд или начальных фаз каждой гармоники от частоты. Домашнее задание Подготовить ответы на вопросы самопроверки. Построить в масштабе сигнал, состоящий из первой и третьей гармоник при соотношении амплитуд U 1 m: U 3 m = 3:1, для случая, когда «нулевые» значения U 1 и U 3 совпадают, а после них следуют значения сигналов U 1 и U 3 одинакового знака. ПРИМЕЧАНИЕ: Рекомендуется сначала построить U 1 и U 3, а затем сложить сигналы в этой же системе координат, результирующий сигнал изобразить другим цветом.
Временная диаграмма третьей гармоники
U 1 m: U 3 m = 3:1
Временная диаграмма суммарного сигнала
Рисунок 6.1 – Получение сигналов негармонической формы путем сложения двух гармонических.
Начертить в масштабе спектральную диаграмму для негармонического сигнала при соотношении U 1 m: U 2 m: U 3 m: U 5 m = 9:7:5:2.
Рисунок 6.2 – Спектральная диаграмма негармонического сигнала
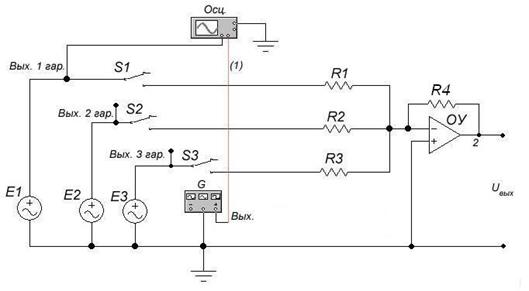
Порядок выполнения работы Собрать схему электрической цепи, представленную на рисунке 6.3 согласно методическому руководству. В данной схеме используются: G - генератор сигнала; Осц. – осциллограф; Е1, Е2, Е3 – генераторы гармонических колебаний соответственно частот f 1, f 2 = 2 f 1, f 3 = 3 f ; S 1, S 2, S 3 – переключатели; ОУ – операционный усилитель.
Рисунок 6.3 - Сумматор
Получить временные диаграммы сигналов различных источников и их сочетаний:
Рисунок 6.4 – Временная диаграмма первой гармоники __________________ (математическая модель)
Рисунок 6.5 – Временная диаграмма второй гармоники ________________ (математическая модель)
Рисунок 6.6 – Временная диаграмма третьей гармоники ________________ (математическая модель)
Рисунок 6.7 – Временная диаграмма суммы первой и второй гармоник __________________________________________________________________ (математическая модель)
Рисунок 6.8 – Временная диаграмма суммы первой и второй гармоник с изменением фазы второй гармоники на 900 ______________________________________________________________ (математическая модель)
Рисунок 6.9 – Временная диаграмма суммы второй и третьей гармоник __________________________________________________________________ (математическая модель)
Рисунок 6.10 – Временная диаграмма суммы второй и третьей гармоник с изменением фазы второй гармоники на 900 _____________________________________________________________ (математическая модель)
Рисунок 6.11 – Временная диаграмма суммы первой и третьей гармоник __________________________________________________________________ (математическая модель)
Рисунок 6.12 – Временная диаграмма суммы первой и третьей гармоник с изменением фазы второй гармоники на 900 _____________________________________________________________ (математическая модель)
Рисунок 6.13 – Временная диаграмма суммы первой, второй и третьей гармоник __________________________________________________________________ (математическая модель)
Контрольные вопросы 1 Как влияет амплитуда и фаза отдельных гармоник на форму несинусоидального сигнала? __________________________________________________________________ __________________________________________________________________
2 Запишите формулу частоты третьей гармоники. __________________________________________________________________
3 Токи каких частот хорошо пропускает катушка индуктивности? Конденсатор? __________________________________________________________________ __________________________________________________________________
Выводы ____________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ «____» ____________ ______г.
Лабораторная работа №7 ИССЛЕДОВАНИЕ РЕЗОНАНСНЫХ ЯВЛЕНИЙ В ПОСЛЕДОВАТЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Цель работы Изучить явления, происходящие в последовательном контуре с R, L, C. Научиться практически определять резонансную частоту, полосу пропускания и добротность последовательного колебательного контура.
|
||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.241.235 (0.005 с.) |

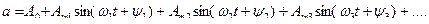
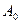 - нулевая гармоника или постоянная составляющая.
- нулевая гармоника или постоянная составляющая. 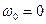
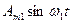 - первая или основная гармоника, частота этой гармоники является частотой всего негармонического колебания
- первая или основная гармоника, частота этой гармоники является частотой всего негармонического колебания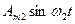 ,
, 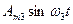 и т.д.- вторая, третья и т.д. или высшие гармоники. Номер гармоники определяется по частоте:
и т.д.- вторая, третья и т.д. или высшие гармоники. Номер гармоники определяется по частоте: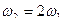 - вторая гармоника
- вторая гармоника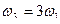 - третья гармоника и т.д.
- третья гармоника и т.д. Временная диаграмма первой гармоники
Временная диаграмма первой гармоники