Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о ферме. Расчет фермСодержание книги
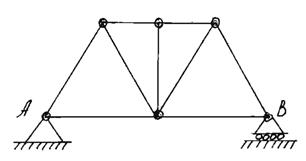
Поиск на нашем сайте Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами (рис. 12).
Рис. 12
Если все стержни фермы лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. Наклонные стержни называются раскосами, вертикальные – стойками. Расстояние между двумя опорами называется пролетом. Расчет ферм выполняется двумя методами: 1) метод вырезания узлов, который сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы; 2) метод сечений (метод Риттера), который состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых требуется определить усилие, составив уравнения равновесия.
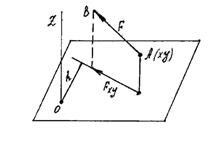
Пространственная система сил Моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью. Чтобы найти момент силы относительно оси Z (рис. 13), надо:
Рис. 13 1) провести плоскость xy, перпендикулярную к оси z; 2) спроектировать силу F на эту плоскость и вычислить величину Fxy; 3) опустить из точки О пересечения оси с плоскостью перпендикуляр на направление Fxy и его длину h; 4) вычислить произведение Fxy · h; 5) определить знак момента. Частные случаи при определении момента: 1)если сила параллельна оси, то ее момент относительно оси равен нулю, так как Fxy = 0; 2) если линия действия силы пересекает ось, то ее момент относительно оси также равен нулю, так как h = 0; 3)если сила перпендикулярна к оси, то ее момент относительно оси равен произведению модуля силы на расстояние между силой и осью. Условия равновесия произвольной пространственной системы сил. Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю. II. Кинематика точки и твердого тела Основные понятия кинематики 1.1. Способы задания движения точки Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил. Кинематически задать движение или закон движения тела (точки) значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени. Системой отсчета называется реальное или условное твердое тело, по отношению к которому определяется положение других движимых тел. Естественный способ задания движения. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая – криволинейным. Закон движения точки вдоль траектории выражается уравнением S = f (t). Чтобы задать движение точки естественным способом,надо знать: 1) траекторию точки; 2) начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета; 3) закон движения точки вдоль траектории в виде S = f (t). Численная величина скорости точки в данный момент времени равна первой производной от расстояния точки по времени:
Численная величина ускорения точки в данный момент времени равна первой производной от скорости:
Координатный способ задания движения Закон движения точки при координатном способе выражается уравнениями: x = f 1(t); y = f 2(t); z = f 3(t). Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени:
Проекции ускорения на оси координат равны первым производным от проекций скоростей или вторым производным от соответствующих координат точки по времени.
|
||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

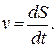
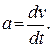

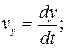
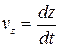 ;
;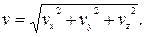

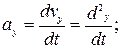
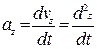 ;
;