Математическое моделирование

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ПРОЦЕССОВ В МАШИНОСТРОЕНИИ

 

Методические указания по выполнению курсовой работы

для студентов очной формы обучения направления

15.03.05 Конструкторско-технологическое обеспечение

машиностроительных производств

 

Краснодар

2016

 

Составитель: канд. техн. наук, проф. В.В. Иосифов

       ст. преп. Н.Л. Клокова

                      

УДК 621

 

Математическое моделирование процессов в машиностроении: методические указания по выполнению курсовой работы для студентов очной формы обучения направления 15.03.05 Конструкторско-технологическое обеспечение машиностроительных производств / Сост.: В.В. Иосифов, Н.Л. Клокова; Кубан. гос. технол. ун-т. Каф. Машиностроения и автомобильного транспорта. – Краснодар, 2016. – 31 с.  

 

 

Изложены цель, тематика и задачи курсовой работы, приведены общие требования и порядок ее выполнения, объем и содержание иллюстративной части и пояснительной записки, приведён список рекомендованных информационных источников.

 

Рецензенты: д-р техн. наук, проф. кафедры МСАТ А.Г. Соколов;

главный инженер МОАО «СЕДИН» В.А. Ююкин

 

 

© КубГТУ, 2016

 

 

78

Содержание

 

1	Нормативные ссылки ……………………………………………….……	4
2	Тематика курсовой работы.………………………………………….......	4
3	Состав и объем курсовой работы ……………………………………….	4
4	Методические рекомендации по выполнению курсовой работы ………………………………………………………….	5
	4.1 Описание моделируемого объекта и постановка задачи моделирования ……………………………………………………	6
	4.2 Корреляционный анализ взаимосвязи между варьирующими признаками объекта ……………………………............	7
	4.3 Анализ и объяснение силы корреляции параметров объекта …………………………………………………………………….	10
	4.4 Выбор типа модели на основе регрессионного анализа ………….	11
	4.5 Анализ разработанных моделей …………………….………………	18
	4.6 Заключение …………………………………………………………..	24
	Список рекомендуемой литературы ……………….………..…………..	24
	Приложение А Форма титульного листа курсовой работы ……….....	25
	Приложение Б Форма задания на курсовую работу……………………	26
	Приложение В Пример оформления реферата ………………….……..	27
	Приложение Г Критические значения корреляции τкрит для уровня значимости α и степени свободы f ….………………….	28
	Приложение Д Значения F-критерия для уровня значимости α = 0,05 и числа степеней свободы f …………………..	29
	Приложение Е Критическое значение R^2 для уровня значимости α, числа переменных (аргументов) x и количества опытов n …………………………….……	30
	Приложение Ж Значения коэффициента Стьюдента (t-критерия)  для уровня значимости α и числа измерений n...….…	31

 

 

Нормативные ссылки

 

В настоящих методических указаниях использованы ссылки на следующие нормативные документы:

    ГОСТ 2.104-2006 ЕСКД. Основные надписи

    ГОСТ 2.105-95 ЕСКД. Общие требования к текстовым документам

ГОСТ 2.120-2013 ЕСКД. Технический проект

    ГОСТ 2.301-68 ЕСКД. Форматы

ГОСТ 7.1-2003 СИБИД. Библиографическая запись. Библиографическое описание. Общие требования и правила составления

 

Тематика курсовой работы

 

Выполнение курсовой работы должно способствовать освоению студентом методологии создания и анализа моделей взаимосвязей характеристик и параметров наземных транспортно-технологических средств методом корреляционного и регрессионного анализа.

Тема курсовой работы определяется заданием и по своему уровню должна соответствовать перспективам развития техники и технологии как на мировом, так и на отечественном уровне.

В общем случае тема курсовой работы формулируется следующим образом: разработка и исследование статистической математической модели взаимосвязи параметров производства машин (по варианту).

В теме курсовой работы могут быть указаны конкретные требования по области и целям анализа (вид процесса, условия исследования и применения т.п).

 

 

Курсовой работы

Моделирование – замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели путем проведения экспериментов над последней.

Моделирование (в широком смысле) является основным методом исследований во всех областях знаний и научно-обоснованным методом оценок характеристик сложных систем, используемых в различных сферах инженерной деятельности.

Объект определяется совокупностью параметров и характеристик. Множество параметров объекта как системы отражает ее внутреннее содержание – структуру и принципы функционирования. Характеристики системы – это ее внешние свойства, которые важны при взаимодействии с другими системами. Характеристики системы находятся в функциональной зависимости от ее параметров.

Статистическое изучение взаимосвязей характеристик и параметров объекта осуществляется методом корреляционного и регрессионного анализа.

Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых должен быть выяснен с помощью теоретического анализа) и оценки факторов, оказывающих наибольшее влияние на результативный признак.

Задачами регрессионного анализа являются выбор типа модели (формы связи), установление степени влияния независимых переменных на зависимую и определение расчётных значений зависимой переменной (функции регрессии).

Во введении к курсовой работе рассматриваются задачи и возможности математического моделирования при оценке взаимосвязи параметров наземных транспортно-технологических средств и анализе возможностей направленного выбора оптимальной модели.

Используется при написании введения информация из достоверных современных информационных источников: технической литературы, статей газет, журналов, ЭБС, интернет-сайтов.

 

Моделирования

Раздел начинается с определения места и назначения моделируемого объекта. Дается описание устройства объекта (схемы сил, распределения температур и т.п.).

Формируется на основе обзора информационных источников массив статистических данных по группе однотипных средств (в соответствии с заданием на курсовую работу).

Выполняется теоретический анализ связей между параметрами объектов причинного характера.

Заканчивается раздел выводами по задачам моделирования.

 

 

Пример

Определить, существует ли связь между количеством часов, затраченных студентом на изучение дисциплины, и финальной экзаменационной оценкой. Таблица 1 иллюстрирует алгоритм определения промежуточных данных для расчета коэффициента корреляции.

 

Таблица 1

Исходные и промежуточные данные для определения r

	A	B	C	D	E
1	Часы изучения, x	Экзамен, y	Оценка, xy	X^2	Y^2
2	3	86	258	9	7396
3	5	95	475	25	9025
4	4	92	368	16	8464
5	4	83	332	16	6889
6	2	78	156	4	6084
7	3	82	246	9	6724
8	Σx=21	Σy=516	Σxy=1835	Σx^2=79	Σy^2=44582

 

.                (2)

 

Как видно, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция.

Таким образом, если обнаруживается, что связь существует, можно прогнозировать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Чем сильнее связь, тем точнее будет прогноз.

Использование Excel для вычисления коэффициентов корреляции

Вычисления коэффициентов корреляции производится с использованием программы Excel с помощью функции КОРРЕЛ со следующими характеристиками:

КОРРЕЛ (массив 1; массив 2),

 

где массив 1 = диапазон данных для первой переменной;

массив 2 = диапазон данных для второй переменной.

Например, на рисунке 3 показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.

 

Рис. 3. Расчет коэффициента корреляции с использованием

программы Excel

 

Для оценки силы корреляции переменных, представленных в задании на курсовое проектирование необходимо по методике, изложенной выше, определить коэффициенты корреляции для всех возможных пар переменных и составить корреляционную матрицу типа приведенной на рисунке 4.

 

	Y1	X1	X2	X3	X…	Xn-1	Xn
Y1	1
X1	ry1,x1	1
X2	ry1,x2	Rx1,x2	1
X3	ry1,x3	Rx1,x3	Rx2,x3	1
X…	ry1,x…	Rx1,x…	Rx2,x…	Rx3,x…	1
Xn-1	ry1,x(n-1)	Rx1,x(n-1)	Rx2,x(n-1)	Rx3,x(n-1)	Rx…,x(n-1)	1
Xn	ry1,xn	Rx1,xn	Rx2,xn	Rx3,xn	Rx..,xn	Rx(n-1),xn	1

 

Рис. 4. Форма корреляционной матрицы

 

Зная коэффициенты корреляции, можно дать качественно-количественную оценку тесноты связи. Используются, например, специальные табличные соотношения (так называемая шкала Чеддока). 

Ее представление имеет следующий вид (табл. 2). 

Таблица 2

Качественная оценка тесноты связи

Величина коэффициента парной корреляции	Характеристика силы связи
До 0,3 0,3−0,5 0,5−0,7 0,7−0,9 0,9−0,99	Практически отсутствует Слабая Заметная Сильная Очень сильная

 

На основании анализа корреляционной матрицы необходимо отобрать факторы, имеющие наибольшую силу связи между У1 и Хi, и слабую связь между Хi и Хj.

В выводах по разделу дать теоретическое объяснение сил связанности факторов на основании описания моделируемого процесса.

Пример

Проанализируем полученное выше уравнение регрессии с использованием рассмотренных статистических критериев.

Проверка по F-критерию. Компьютерный расчет выдал величину F _расч, равную 16,99 (см. рис.10). Для анализа уравнения будем пользоваться величиной F _расч, обратной представленной Excel. Она составит 1:16,99 = = 0,06. Отыщем по эталонной таблице (прил. Д) критическую величину F _крит  при условии, что для числителя степень свободы   f ₁ = k, т.е. составит 2 (число воздействующих факторов равно 2), а для знаменателя

  f ₂ = n − k −1 = 20 − 2 − 1= 17. Тогда будем иметь следующие значения для F _крит: 3,6 (для α = 0,05), 6,2 (α = 0,01) и 10,5 (α = 0,001). Понятно, что для всех рассмотренных вероятностей выполняется соотношение F _расч<F_крит, поэтому уверенно можно говорить о высокой степени адекватности анализируемого уравнения.

Проверку с использованием уровня значимости α (в Excel этот показатель именует как р). На рис.10 находим позицию «Значимость F». Там указана величина 8,84Е-5, т.е. это число 8,84, перед которым стоит 5 нулей. Фактически можно признать, что α = 0,000. Это говорит о том, что действительно обнаруживается устойчивая зависимость рассматриваемой функции у от воздействующих факторов х ₁ и х ₂, т.е. y не является чисто случайной величиной. Но пока неизвестно, какие именно факторы (оба х ₁ и х ₂или какой-то один из них) реально участвует в прогнозировании, но доподлинно понятно, что по крайней мере один из них влияет непременно.

Проверка по коэффициенту детерминации R ^2. По расчетам, коэффициент детерминации R ²_расч составляет 0,67, или 67 %. Таблица для тестирования на уровне значимости 5 % в случае выборки n = 20 и числа переменных k = 2 дает критическое значение R ²_крит = 0,297 (прил. Е). Поскольку выполняется соотношение R ²_расч^> R ²_крит, то с вероятностью 95 % можно утверждать о наличии значимости данного уравнения регрессии.

Кстати заметим, что для наших обстоятельств (n = 20, k = 2) можно оценить критическое значение R ²_крит для α = 0,01 (высокая значимость) и α = 0,001 (высшая степень значимости). В этом случае R ²_крит составляет соответственно 0,384 и 0,517, что, как видно, все равно остается меньше расчетного показателя R ²_расч, т.е. 0,67. Из чего следует заключить, что обсуждаемое нами уравнение действительно характеризуется очень высокой степенью значимости.

Как видно, все три рассмотренных приема статистической проверки дают одинаковый результат. В этом примере мы воспользовались подобным разнообразием способов анализа только с одной целью – дать представление о существующих методах такой проверки. На практике наиболее распространенным методом считается выполнение проверки по F -критерию. 

Итак, проведена проверка на значимость самого уравнения, т.е. установлено, что существует взаимосвязь между параметром у и переменными х_k. Однако нам пока неясно, каково влияние конкретных факторов х ₁ и х ₂ на исследуемую функцию у: действуют ли оба фактора или только какой-то один из них. Поэтому предстоит определить значимость отдельных коэффициентов регрессии b ₁ и b ₂. Для этой цели используется так называемый t- тест.

Проверка на адекватность коэффициентов регрессии

Проверку на адекватность коэффициентов регрессии рекомендуется проводить по следующим эквивалентным методам.

Использование t-критерия. Необходимые расчеты делает Excel, который выдает значения показателя t. Анализируемый коэффициент считается значимым, если его t-критерий по абсолютной величине превышает 1,96, что соответствует уровню значимости 0,05 (табл. 3). В нашем примере имеем для коэффициентов b ₀, b ₁ и b ₂ следующие показатели критерия Стьюдента: t_{b 0} = 2,09; t_{b 1} = 2,59 и t_{b 2} = 2,57. Из всего вышесказанного следует, что значимыми оказываются все коэффициенты нашегоуравнения.

Использование уровня значимости. В этом случае оценка проводится путем анализа показателя р, т.е. уровня значимости α. Коэффициент признается значимым, если рассчитанное для него р -значение (эти данные выдает Excel) меньше (или равно) 0,05 (т.е. для 95 %-й доверительной вероятности). Показатель р составляет для коэффициентов b ₀, b ₁ и b ₂ следующие величины: р _{b 0} =0,05; р _{b 1}=0,02 и р _{b 2} =0,02. 

Эти данные позволяют также заключить, что все рассмотренные коэффициенты статистически значимы. Иначе говоря, можно сделать вывод о неслучайном характере влияния всех изученных параметров. 

Таким образом, проверка обоими методами дает вполне согласованные результаты. Поэтому в окончательном виде наше уравнение регрессии (для уровня значимости 0,05) следует записать так

ŷ = 1,61 + 0,06 x ₁ + 0,07 x ₂.

Сравнительная оценка степени влияния факторов

Для решения данной задачи используем метод сравнения стандартизованных коэффициентов регрессии.  

В общем случае все коэффициенты регрессии b ₁, b _2, …, b_k могут быть выражены в разных единицах измерения. Тем самым непосредственное их сравнение становится фактически некорректным, поскольку формально меньший по величине коэффициент на деле может оказаться важнее большего. Стандартизованные коэффициенты регрессии позволяют решить эту проблему за счет представления коэффициентов регрессии в некоторых кодированных единицах измерения.

Стандартизованный коэффициент регрессии вычисляется путем умножения коэффициента регрессии b_i на стандартное отклонение S_n (для х -переменных обозначим его как S_xk) и деления полученного произведения на S_у. Это означает, что каждый стандартизованный коэффициент регрессии измеряется как величина b_i S_xk / S_у. Применительно к нашему примеру получим следующие результаты (табл. 6). 

 

Таблица 6

Стандартизованные коэффициенты регрессии

Статистические характеристики	y	X1	X2
Стандартные отклонения	Sу = 1,06	SX1 = 8,26	SX2 = 7,25
Коэффициенты регрессии	-	b 1 = 0,06	b 2 = 0,07
Стандартизованные коэффициенты регрессии	-	b 1 SX1 / Sу = 0,06·8,26/1,06=0,47	b 2 SX2 / Sу = = 0,07·7,25/1,06=0,48

 

После проделанных расчетов мы можем на объективном основании сопоставить полученные коэффициенты. Для обоих анализируемых факторов стандартизованные коэффициенты практически одинаковы.

Таким образом, приведенное сравнение абсолютных величин стандартизованных коэффициентов регрессии позволяет получить наглядное представление о важности рассматриваемых факторов. Еще раз напомним, что эти результаты не являются идеальными, поскольку не в полной мере отражают реальное влияние исследуемых переменных (мы оставляем без внимания факт возможного взаимодействия этих факторов, что может исказить первоначальную картину).

В целом же проведенный регрессионный анализ дает основание оценить влияние рассмотренных факторов на функцию. Вместе с тем ставятся задачи на доработку модели: явно неприняты во внимание все факторы (33 % приходится на неучтенные причины).

Заключение

В заключении курсовой работы необходимо кратко отразить качественные и количественные результаты выполненной работы. Отразить положительные и отрицательные моменты и привести рекомендации по устранению недостатков.

 

 

Список рекомендуемой литературы

1. Ратнер С.В., Киселева Н.В. Программные статистические комплексы в менеджменте качества: учеб. пособие. Краснодар: Кубан. гос. ун-т, 2011. 185 с.

2. Барботько А. И. Основы теории математического моделирования: учеб. пособие для студ. вузов, обуч. по напр. «Конструкторско-технологическое обеспечение машиностроительных производств» / А.И. Барботько [и др.]. Старый Оскол: ТНТ, 2013. 212 с. 

3. Зарубин В. С. Математическое моделирование в технике: учебник для студентов высших технических учебных заведений. – Изд. 3-е. М.: Изд-во МГТУ им. Н. Э. Баумана, 2010. 496 с. 

4. Казаков Ю.М., Аверченков В.И. Автоматизация проектирования технологических процессов: учеб. пособие для вузов. М.: ФЛИНТА, 2011. 229 с.

5. Моделирование систем: учебник рек. Мин. обр. РФ / С. И. Дворецкий [и др.]. М.: Академия, 2009. 317 с.

6. Шаламов В.Г. Математическое моделирование при резании металлов: учеб. пособие. Челябинск: Изд-во ЮУрГУ, 2007. 134 с.

Приложение А

КУРСОВАЯ РАБОТА

по дисциплине «Математическое моделирование процессов

В машиностроении»

 

на тему _________________________________________________________

 

Выполнил(а) студент(ка) __________________ курса _____ группы ______

 (фамилия, имя, отчество)

 

Допущена к защите _____________________

(дата)

 

Руководитель (нормоконтролер) работы _____________________________

(должность, подпись, дата, расшифровка подписи)

 

Защищена ___________________                    Оценка__________________

(дата)

 

Члены комиссии ________________________________________________

_______________________________________________________________

_______________________________________________________________

_______________________________________________________________

(должность, подпись, дата, расшифровка подписи)

 

Краснодар

20___ г.

 

Приложение Б

Форма задания на курсовую работу

 

ЗАДАНИЕ

На курсовую работу

 

Студенту (ке) ______________________ курса _______ группы __________

Тема работы _____________________________________________________

________________________________________________________________

План работы:

1. ______________________________________________________________

2. ______________________________________________________________

3. ______________________________________________________________

 

Объем работы:

а) пояснительная записка ___________________ с.

б) иллюстративная часть ____________________ лист(ов)

Рекомендуемая литература ________________________________________

________________________________________________________________

________________________________________________________________

Срок выполнения:                          с «____» ____ по «____» _____ 20__ г.

Срок защиты:                                                                «____» _____ 20__ г.

Дата выдачи задания:                                                   «____» _____20__ г.

Дата сдачи работы на кафедру:                                   «____» _____20__ г.

Руководитель работы  __________________________________

       (подпись)

Задание принял студент ________________________________

(подпись)

Приложение В

Пример оформления реферата

Реферат

Курсовая работа 35 с., 8 рис., 12 табл., 15 источников, 3 приложения,

иллюстративная часть – 3 листа формата А1.

 

МАШИНОСТРОЕНИЕ, ПАРАМЕТРЫ МАШИН, МОДЕЛИРОВАНИЕ, КОРРЕЛЯЦИОННЫЙ АНАЛИЗ, РЕГРЕССИОННЫЙ АНАЛИЗ, АДЕКВАТНОСТЬ МОДЕЛИ, ПРОГНОЗИРОВАНИЕ

 

Объект: технологический процесс.

Цель: создание математической модели связи параметров машины, отвечающей требованиям адекватности.

Выполнен анализ и прогнозирование связей параметров машины.

Определены взаимосвязи параметров методом корреляционного анализа.

Выявлены параметры, имеющие высокую корреляцию с выходной функцией.

Разработана и исследована на адекватность регрессионная модель процесса.

Определены эффективные направления воздействия на процесс.

Приложение Г

 

Критические значения корреляции τ _крит    для уровня значимости

α и степени свободы   f

                              

 

Приложение Д

Значения F- критерия для уровня значимости

α = 0,05 и числа степеней свободы f          

 

 

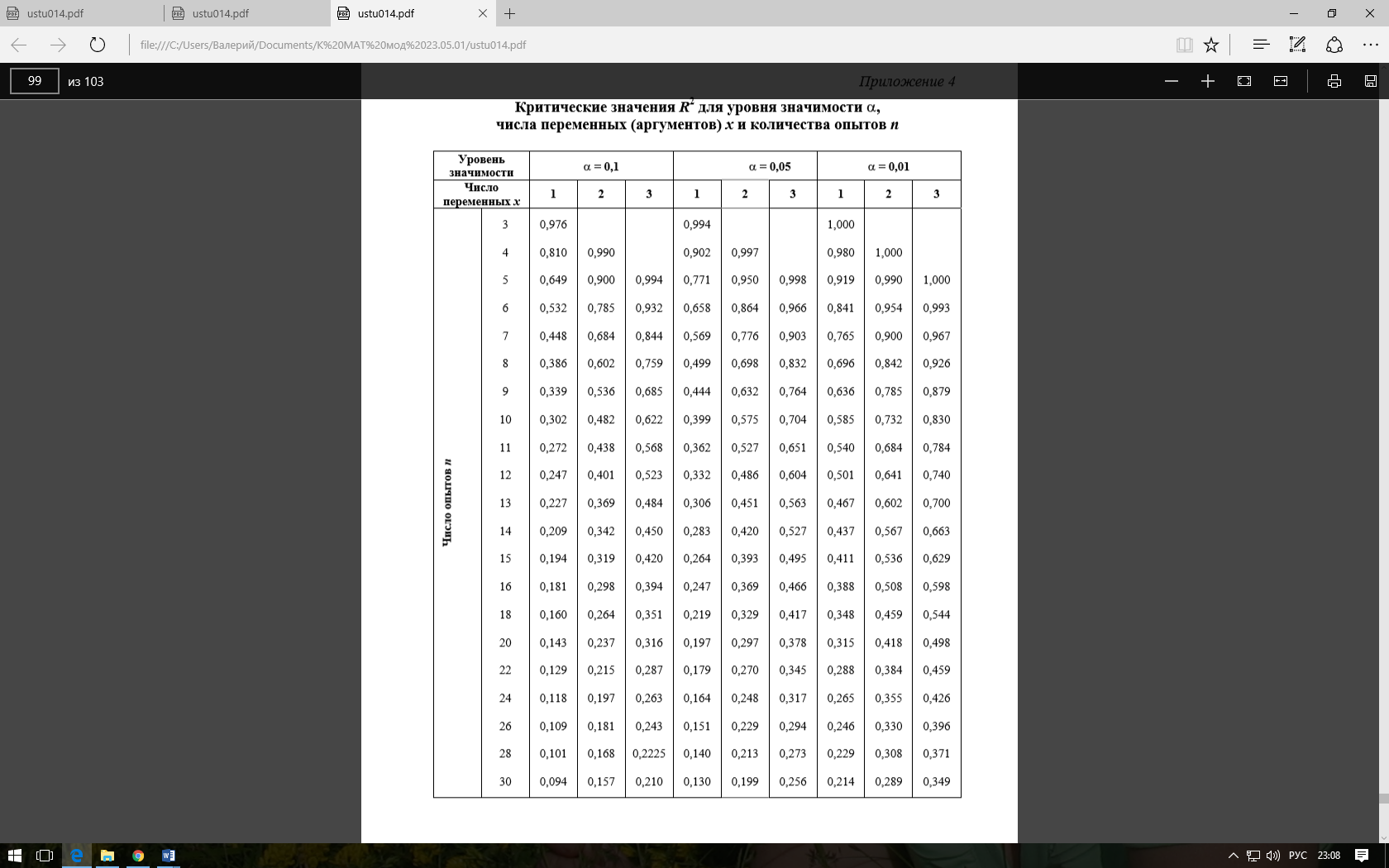
Приложение Е

Критическое значение R ² для уровня значимости α, числа

переменных (аргументов) x и количества опытов n

Приложение Ж

 

Значения коэффициента Стьюдента (t -критерия) для уровня значимости α и числа измерений n

 

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ПРОЦЕССОВ В МАШИНОСТРОЕНИИ

 

Методические указания по выполнению курсовой работы

для студентов очной формы обучения направления

15.03.05 Конструкторско-технологическое обеспечение

машиностроительных производств

 

Краснодар

2016

 

Составитель: канд. техн. наук, проф. В.В. Иосифов

       ст. преп. Н.Л. Клокова

                      

УДК 621

 

Математическое моделирование процессов в машиностроении: методические указания по выполнению курсовой работы для студентов очной формы обучения направления 15.03.05 Конструкторско-технологическое обеспечение машиностроительных производств / Сост.: В.В. Иосифов, Н.Л. Клокова; Кубан. гос. технол. ун-т. Каф. Машиностроения и автомобильного транспорта. – Краснодар, 2016. – 31 с.  

 

 

Изложены цель, тематика и задачи курсовой работы, приведены общие требования и порядок ее выполнения, объем и содержание иллюстративной части и пояснительной записки, приведён список рекомендованных информационных источников.

 

Рецензенты: д-р техн. наук, проф. кафедры МСАТ А.Г. Соколов;

главный инженер МОАО «СЕДИН» В.А. Ююкин

 

 

© КубГТУ, 2016

 

 

78

Содержание

 

1	Нормативные ссылки ……………………………………………….……	4
2	Тематика курсовой работы.………………………………………….......	4
3	Состав и объем курсовой работы ……………………………………….	4
4	Методические рекомендации по выполнению курсовой работы ………………………………………………………….	5
	4.1 Описание моделируемого объекта и постановка задачи моделирования ……………………………………………………	6
	4.2 Корреляционный анализ взаимосвязи между варьирующими признаками объекта ……………………………............	7
	4.3 Анализ и объяснение силы корреляции параметров объекта …………………………………………………………………….	10
	4.4 Выбор типа модели на основе регрессионного анализа ………….	11
	4.5 Анализ разработанных моделей …………………….………………	18
	4.6 Заключение …………………………………………………………..	24
	Список рекомендуемой литературы ……………….………..…………..	24
	Приложение А Форма титульного листа курсовой работы ……….....	25
	Приложение Б Форма задания на курсовую работу……………………	26
	Приложение В Пример оформления реферата ………………….……..	27
	Приложение Г Критические значения корреляции τкрит для уровня значимости α и степени свободы f ….………………….	28
	Приложение Д Значения F-критерия для уровня значимости α = 0,05 и числа степеней свободы f …………………..	29
	Приложение Е Критическое значение R^2 для уровня значимости α, числа переменных (аргументов) x и количества опытов n …………………………….……	30
	Приложение Ж Значения коэффициента Стьюдента (t-критерия)  для уровня значимости α и числа измерений n...….…	31

 

 

Нормативные ссылки

 

В настоящих методических указаниях использованы ссылки на следующие нормативные документы:

    ГОСТ 2.104-2006 ЕСКД. Основные надписи

    ГОСТ 2.105-95 ЕСКД. Общие требования к текстовым документам

ГОСТ 2.120-2013 ЕСКД. Технический проект

    ГОСТ 2.301-68 ЕСКД. Форматы

ГОСТ 7.1-2003 СИБИД. Библиографическая запись. Библиографическое описание. Общие требования и правила составления

 

Тематика курсовой работы

 

Выполнение курсовой работы должно способствовать освоению студентом методологии создания и анализа моделей взаимосвязей характеристик и параметров наземных транспортно-технологических средств методом корреляционного и регрессионного анализа.

Тема курсовой работы определяется заданием и по своему уровню должна соответствовать перспективам развития техники и технологии как на мировом, так и на отечественном уровне.

В общем случае тема курсовой работы формулируется следующим образом: разработка и исследование статистической математической модели взаимосвязи параметров производства машин (по варианту).

В теме курсовой работы могут быть указаны конкретные требования по области и целям анализа (вид процесса, условия исследования и применения т.п).