
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитные и механические аналогии.Содержание книги
Поиск на нашем сайте В теме " Электромагнитные колебания " рассматривается электромагнитный процесс, возникающий при разрядке конденсатора через катушку индуктивности и делается вывод о колебательном характере этого процесса. Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями, например с колебаниями тела, закрепленного на пружине. Сходство относится не к природе самих величин, которые периодически изменяются, а к процессам периодического изменения различных величин. При механических колебаниях периодически изменяются координата тела x и проекции его скорости Подобно тому как вследствии инертности тело лишь постепенно увеличивает скорость под действием силы и эта скорость после прекращения действия силы не становится сразу равной нулю, электрический ток в катушке за счет явления самоиндукции увеличивается под действием напряжения постепенно и не исчезает сразу, когда это напряжение становится равным нулю. Индуктивность контура L играет туже роль, что и масса тела m в механике. Соответственно кинетической энергии тела Зарядке конденсатора от батареи соответствует сообщение телу, прикрепленному к пружине, потенциальной энергии Сравнивая это выражение с энергией конденсатора Возникновение в электрической цепи тока i за счет разности потенциалов соответствующих появлению в механической колебательной системе скорости
Рассмотренные выше колебания являются свободными. Здесь не учтено, что в любой реальной механической системе существуют силы трения. Таким образом, соответствие между механическими и электрическими величинами при колебательных процессах можно представить в виде таблицы 1
Выведем уравнение свободных незатухающих электромагнитных колебаний в контуре и колебаний горизонтального пружинного маятника. Применяя к пружинному маятнику закон сохранения энергии, получим равенство:
Так как
Следует заметить, что уравнение (2) так же следует из закона сохранения энергии. В уравнении (2) i = q ' - мгновенное значение силы тока, qmax - максимальный заряд на конденсаторе (он не должен вызвать пробоя). Делаем вывод о зависимости силы тока от величины заряда и находим значение максимальной силы тока:
Как видно формально с точки зрения математики уравнения (1) и (2) являются одинаковыми. Решаем уравнение (2): производная полной энергии по времени равна нулю, так как энергия постоянна. Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей.
Физический смысл уравнения (3) состоит в том, что скорость изменения энергии магнитного поля по модулю равна скорости изменения энергии электрического поля; знак “минус” указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля убывает (и наоборот). Поэтому полная энергия не меняется. Вычисляя обе производные получаем:
так как
получаем
Уравнение (4) является основным уравнением, описывающем процессы в колебательном контуре.
Рассмотрим колебания вертикального пружинного и математического маятников.
где X0= mg/ k - статическое растяжение пружины (потенциальную энергию груза в поле силы тяжести отсчитываем от уровня равновесия груза, обозначенного на рис. 2 пунктиром). Учитывая, что
Как видно уравнения колебаний горизонтального и вертикального пружинных маятников одинаковы. Ускорение свободного падения g, имеющееся в уравнении (5), отсутствует в полученном уравнении колебаний. Следовательно, колебания груза на пружине не зависят от g и одинаковы, например, на Земле и Луне. Хотя в дифференциальные уравнения (1) и (6) входят разные величины, математически они эквивалентны. По аналогии с уравнением (4) описывающем процессы в колебательном контуре, запишем уравнение колебания пружинного маятника:
получим
Отклоним теперь математический маятник длиной l (рис. 3) от положения равновесия на длину дуги sm<<l и отпустим. Мгновенная высота подъема маятника
рис.3
так как при a<<1 можно считать
или
По аналогии с формулами (4) и (7) x®q®s; S``= - Различие уравнений (1), (6) и (9) состоит только в обозначениях и физическом смысле входящих в них величин. Если не предполагать sm<<l (соответственно am= Процессы в колебательном контуре станут понятнее учащимся при рассмотрении преобразований энергий, которые происходят при колебаниях, используя таблицу 2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-13; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.86 (0.01 с.) |

 , а при электромагнитных колебаниях меняются заряд конденсатора q и сила тока в цепи i. Одинаковый характер изменения величин (механических и электрических) объясняется тем, что имеется аналогия в условиях, при которых порождаются механические и электромагнитные колебания. Возвращение к положению равновесия тела на пружине вызывается силой упругости F, пропорциональной смещению тела от положения равновесия. Коэффициентом пропорциональности является жесткость пружины k. Разрядка конденсатора (появление тока) обусловлена напряжением U между пластинами конденсатора, которое пропорционально заряду q. Коэффициентом пропорциональности является величина
, а при электромагнитных колебаниях меняются заряд конденсатора q и сила тока в цепи i. Одинаковый характер изменения величин (механических и электрических) объясняется тем, что имеется аналогия в условиях, при которых порождаются механические и электромагнитные колебания. Возвращение к положению равновесия тела на пружине вызывается силой упругости F, пропорциональной смещению тела от положения равновесия. Коэффициентом пропорциональности является жесткость пружины k. Разрядка конденсатора (появление тока) обусловлена напряжением U между пластинами конденсатора, которое пропорционально заряду q. Коэффициентом пропорциональности является величина  , обратная емкости, так как
, обратная емкости, так как  =
=  отвечает энергия магнитного поля тока
отвечает энергия магнитного поля тока  , а импульсу тела mv отвечает поток магнитной индукции Li.
, а импульсу тела mv отвечает поток магнитной индукции Li. при смещении тела на расстояние
при смещении тела на расстояние  от положения равновесия (рис. 1,а).
от положения равновесия (рис. 1,а). , замечаем, что жесткость k пружины играет при механическом колебательном процессе такую же роль, как величина
, замечаем, что жесткость k пружины играет при механическом колебательном процессе такую же роль, как величина  .
. под действием силы упругости пружины (рис.1,б). Моменту, когда конденсатор разрядится, а сила тока достигнет максимума, соответствует прохождение тела через положение равновесия с максимальной скоростью (рис.1.в). Далее конденсатор начнет перезаряжаться, а тело смещаться влево от положения равновесия (рис.1,г). По прошествии половины периода Т конденсатор полностью перезарядится и сила тока станет равной нулю. Этому состоянию соответствует отклонение тела в крайнее левое положение, когда его скорость равна нулю (рис.1,д).
под действием силы упругости пружины (рис.1,б). Моменту, когда конденсатор разрядится, а сила тока достигнет максимума, соответствует прохождение тела через положение равновесия с максимальной скоростью (рис.1.в). Далее конденсатор начнет перезаряжаться, а тело смещаться влево от положения равновесия (рис.1,г). По прошествии половины периода Т конденсатор полностью перезарядится и сила тока станет равной нулю. Этому состоянию соответствует отклонение тела в крайнее левое положение, когда его скорость равна нулю (рис.1,д). +
+  , где
, где ,
, 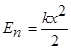 , тогда имеем
, тогда имеем (1)
(1)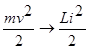 и
и  получаем
получаем
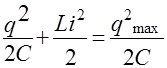 =const (2)
=const (2)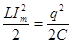 ;
; 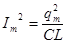 Откуда
Откуда при q=0.
при q=0. или
или (3)
(3)

 , тогда
, тогда и
и 

 (4)
(4) и выводимая на его основе формула потенциальной энергии пружины.)
и выводимая на его основе формула потенциальной энергии пружины.) Рис.2
Рис.2 (5)
(5) и
и  , получим уравнение колебаний
, получим уравнение колебаний

 =соnst
=соnst  ;
; 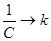 ;
; 
 , (7)
, (7)
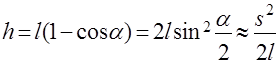
 , а s=la. По закону сохранения энергии имеем:
, а s=la. По закону сохранения энергии имеем: , где
, где 

 =const (8)
=const (8)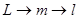 ;
;  получаем:
получаем: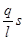 (9)
(9) <<1 рад.), то получится сложное уравнение, решить которое в рамках школьного курса невозможно. Оно будет описывать колебания, период которых зависит от амплитуды. Строго говоря, период колебаний маятника всегда зависит от am, однако при sm<<l рад. этой зависимостью можно пренебречь.
<<1 рад.), то получится сложное уравнение, решить которое в рамках школьного курса невозможно. Оно будет описывать колебания, период которых зависит от амплитуды. Строго говоря, период колебаний маятника всегда зависит от am, однако при sm<<l рад. этой зависимостью можно пренебречь.
 ;
; 
 ;
; 




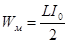
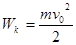

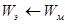




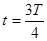

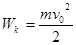



 ; Wм=0
; Wм=0
 ; Wk=0
; Wk=0



