
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение аналитического выражения функции плотности распределения вероятности ⇐ ПредыдущаяСтр 3 из 3
По полученным нами значениям и по виду гистограммы и полигона можно выдвинуть гипотезу о том, что вид нашего распределения треугольный. Проверим эту гипотезу также и аналитически, вычислив точки полигона с помощью метода наименьших квадратов. Метод наименьших квадратов применяется для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений. Метод наименьших квадратов - простой и быстрый способ получить неизвестные параметры в функциональных зависимостях и оценить их погрешности. Пусть ожидаемая теоретическая зависимость y=f(x), и мы получили ряд значений (x i, f (x i)). Тогда величину ошибки можно оценить как сумму квадратов всех отклонений от теоретической зависимости [12]:
где
Таким образом, любая функция определяемая методом наименьших квадратов проходит через координаты
После этого величины a и b вычисляются по формулам [9]:
Произведя расчеты, получили два уравнения и точки, по которым и построили кривую.
)у=133х+11,39 2) у=-133х+73
Кривая, найденная аналитически, с небольшим отклонением совпадает с экспериментальной кривой, поэтому можно предположить, что наиболее целесообразно будет доказывать выдвинутую нами гипотезу.
Рисунок 1.3. Наложение аналитически найденного полигона на экспериментальный. 1 - экспериментально найденный полигон частотной гистограммы, 2 - аналитически найденный полигон.
Критерий Пирсона
Известен целый ряд критериев согласия. Их используют в качестве способа оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки. Наибольшее распространение в практике получил критерий Пирсона [13]. Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения. Идея этого метода состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенной на основе распределения, совпадение с которым определяется. Использование критерия Пирсона возможно при большом числе измерений (n>50) и заключается в вычислении величины
где m - число интервалов разбиения;
n-сумма экспериментальных значений частот в i -том интервале. Экспериментальные данные частот даны нам в Таблице 1.3. для того, чтобы вычислить теоретические данные частот
Получим Если вычисленная по опытным данным мера расхождения Доверительный интервал
Доверительный интервал - это допустимое отклонение наблюдаемых значений от истинных. Размер этого допущения определяется исследователем с учетом требований к точности информации. Если увеличивается допустимая ошибка, размер выборки уменьшается, даже если уровень доверительной вероятности останется равным 95%.
Доверительный интервал показывает, в каком диапазоне расположатся результаты выборочных наблюдений. Для того, что бы найти доверительный интервал, проводим нормировку наших функций, полученных аналитическим путем [5]:
Получаем нормировочный множитель равный 0,075, умножив наши функции на этот множитель, находим доверительный интервал с вероятностью P=0,95:
Преобразовав, получаем квадратное уравнение:
Откуда получаем, что Δ=0,244. Аналогичным образом находим доверительный интервал с вероятностью P=0,9, он будет равен Δ=0,215. Заключение
Итак, подводя итоги, нужно обобщить полученные в ходе работы результаты. Обработав массив данных, мы рассчитали такие значения как: Таблица 1.4 Полученные результаты
Также построили гистограмму и полигон данного нам массива и выдвинули гипотезу о виде распределения. В данной работе вид распределения был взят как треугольный симметричный. Проверив выдвинутую нами гипотезу аналитическим методом с помощью метода наименьших квадратов и с помощью критерия согласия, за который взяли критерий Пирсона, мы убедились, что выдвинутая гипотеза верна. Затем нашли доверительный интервал и доказали, что с увеличением значения вероятности доверительный интервал увеличивается, так как при P=0,9 Δ=0,215 а при P=0,95 Δ=0,244. Список используемой литературы 1. ГОСТ 16263 - 70 ГСИ. Метрология. Термины и определения. - Введен 01.01.2001 взамен ГОСТ 16263-70. - ВНИИКИ Госстандарта России, 2001. - 46 с. - (Действующий стандарт). 2. Сергеев, А. Г. Метрология: история, современность, перспективы: учебное пособие для вузов по направлению «Стандартизация, сертификация и метрология» / А. Г. Сергеев. - М.: Университетская книга: Логос, 2009. - 384 . Димов, Ю. В. Метрология, стандартизация и сертификация: учебник для вузов / Ю. В. Димов. - 3 - е изд. - СПБ.: Питер, 2010. - 464 с.: ил. . Сергеев А. Г. Метрология, стандартизация и сертификация: Учебное пособие для вузов / А. Г. Сергеев, М. В. Латышев, В. В. Терегея. - М.: Логос, 2005. - 560с.: ил. . Радкевич, Я. М. Метрология, стандартизация и сертификация: учебник для вузов / Я. М. Радкевич, А. г. Схиртладзе, Б. И. Лактионов. - 3-е изд. перераб. и доп. - М.: Высш. шк., 2007. - 791 с.: ил. . Гмурман, В. Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов / В. Е. Гмурман. - 12 - е изд., перераб. - М.: Высшее образование, 2006. - 479 с. . Дубровский, П. В. Современные методы метрологического обеспечения инновационных и организационно-технических процессов: учебно-методический комплекс / П. В. Дубровский, С. В. Голякова. - Ульяновск: УлГУ, 2006. - 116 с. . Кочетков, Е. С. Теория вероятностей и математическая статистика: Учебник / Е. С. Кочетков, С. О. Смерчинская, В. В. Соколов. - М.: ФОРУМ: ИНФРА - М, 2005. - 240 с.: ил.
. Булярский, С. В. Метрология: методические указания к выполнению расчетно-графических работ / С.В. Булярский [и др.]. - Ульяновск: УлГУ, 2009. - 92 с. . Павлов, С. В. Теория вероятностей и математическая статистика: учебное пособие / С. В. Павлов. - М.: РИОР, 2006. - 186с. . Никифоров, А. Д. Метрология, стандартизация и сертификация: учеб. пособие для сред. проф. образования по спец. техн. профиля / А. Д. Никифоров, Т. А. Бакиев. - М.: Высшая школа, 2005. - 422 с. . Кошевая, И. П. Метрология, стандартизация, сертификация: учебник для образовательных учреждений сред. профильного образования / И. П. Кошевая, А. А. Канке. - М.: Форум: ИНФРА - М, 2007. - 416 с. . Юсупов, Р. А. Теория вероятностей и математическая статистика: учебное пособие для вузов / Р. А. Юсупов. - Астрахань: АГТУ, 2000. - 186 с. . Сергеев, А.Г. Метрология. Карманная энциклопедия студента: Учебное пособие для студентов высших и средних специальных заведений / А. Г. Сергеев, В. В. Крохин. - М.: Логос, 2001.- 376с.: ил. . Сергеев, А. Г. Метрология: учебник / А. Г. Сергеев. - М.: Логос, 2004. - 288 с.: ил.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-14; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.136 (0.015 с.) |
 , (2.2)
, (2.2) - среднее значение х. Для достижения наилучшей точности эта ошибка должна быть минимальной. Возьмем от полученной суммы по всем параметрам производные и приравняем их к нулю - получим систему уравнений для этих параметров, решениями которой и будут наиболее вероятные их значения. В случае линейной зависимости (а практически любая зависимость может быть линеаризована) имеем:
- среднее значение х. Для достижения наилучшей точности эта ошибка должна быть минимальной. Возьмем от полученной суммы по всем параметрам производные и приравняем их к нулю - получим систему уравнений для этих параметров, решениями которой и будут наиболее вероятные их значения. В случае линейной зависимости (а практически любая зависимость может быть линеаризована) имеем: (2.3)
(2.3) ,
,  , то есть через центр тяжести экспериментальных данных. Коэффициент a определяет наклон искомой зависимости относительно оси аргумента. Метод наименьших квадратов необратен, то есть нельзя менять местами оси. Этот метод очень чувствителен к наличию грубого промаха, если грубый промах не исключить, то погрешность в определении коэффициента будет составлять 96%. Также для нахождения параметров а и b можно по этому методу предварительно вычислить следующие суммы [9]:
, то есть через центр тяжести экспериментальных данных. Коэффициент a определяет наклон искомой зависимости относительно оси аргумента. Метод наименьших квадратов необратен, то есть нельзя менять местами оси. Этот метод очень чувствителен к наличию грубого промаха, если грубый промах не исключить, то погрешность в определении коэффициента будет составлять 96%. Также для нахождения параметров а и b можно по этому методу предварительно вычислить следующие суммы [9]: (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7)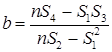 (2.8)
(2.8) (2.9)
(2.9)
 (хи - квадрат) [14]:
(хи - квадрат) [14]: , (2.10)
, (2.10) ,
,  - экспериментальные и теоретические значения частот в i -том интервале разбиения;
- экспериментальные и теоретические значения частот в i -том интервале разбиения; - значения вероятностей в том же интервале разбиения, соответствующие выбранной модели распределения;
- значения вероятностей в том же интервале разбиения, соответствующие выбранной модели распределения; , нам нужно рассчитать интегралы от функций на всех интервалах аналитически построенного полигона. Это можно сделать при помощи программы MathCAD. То есть:
, нам нужно рассчитать интегралы от функций на всех интервалах аналитически построенного полигона. Это можно сделать при помощи программы MathCAD. То есть:
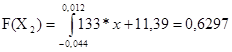
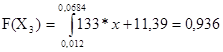








 =3,018. Используя функции программы Microsoft Excel можно вычислить таблично значение критерия. Получаем
=3,018. Используя функции программы Microsoft Excel можно вычислить таблично значение критерия. Получаем  =15,507.
=15,507. меньше определенного из таблицы значения
меньше определенного из таблицы значения  , то гипотеза о совпадении экспериментального и выбранного теоретического распределений принимается [15]. В моем случае
, то гипотеза о совпадении экспериментального и выбранного теоретического распределений принимается [15]. В моем случае  <
<  , следовательно, выбранную гипотезу можно принять за верную.
, следовательно, выбранную гипотезу можно принять за верную. (2.11)
(2.11)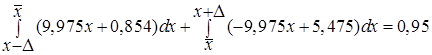

 = 0,21
= 0,21
 =0,000031
=0,000031
 =0,00061
=0,00061
 =2,5
=2,5




