
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Редуктора (колеса косозубые)Содержание книги Поиск на нашем сайте При расчете передач следует считать, что редуктор выполняется в виде самостоятельного механизма, поэтому в соответствии с ГОСТ 21354-87 основным параметром передачи является межосевое расстояние аw, мм
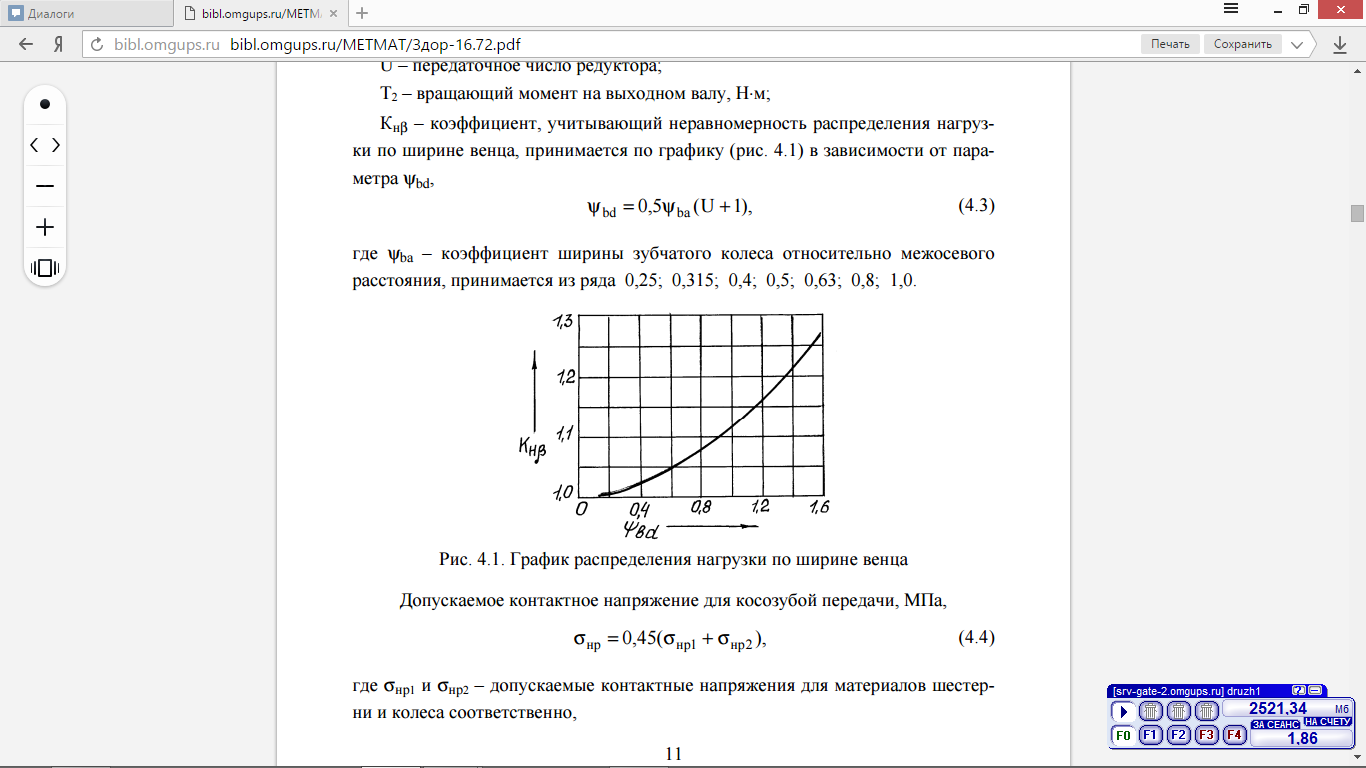
где K а = 430 – вспомогательный коэффициент для косозубых передач; U –передаточное число редуктора; Т2 – вращающий момент на выходном валу, Н∙м; ψ ba – коэффициент ширины венца зубчатого колеса относительно межосевого расстояния, принимаем ψba = 0,5; К H β –коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, принимаемый из графика (рисунок 2) в зависимости от параметра ybd
К H β =1,12.
Рисунок 2 – График распределения нагрузки по ширине венца
Допускаемое контактное напряжение σнр для косозубой передачи, МПа
где s нр1, s нр2 – допускаемые контактные напряжения для материалов шестерни и колеса соответственно. Напряжения sнр1, sнр2рассчитываются по формулам
где SН = 1,1 – коэффициент запаса прочности для зубчатых колес с однородной структурой материала; Z N 1, Z N 2 – коэффициенты долговечности шестерни и колеса; ZR – коэффициент, учитывающий влияние исходной шероховатости сопряжённых поверхностей зубьев; ZV – коэффициент, учитывающий влияние окружной скорости; ZL – коэффициент, учитывающий влияние смазочного материала; ZX – коэффициент, учитывающий размер зубчатого колеса. При выполнении расчетов принимаем Пределы контактной усталости поверхностей зубьев, МПа
где НВ 1, НВ 2 – твердость материалов шестерни и колеса соответственно.
Коэффициенты долговечности шестерни и колеса
где NHlim 1, NHlim 2 – базовые числа циклов напряжений, соответствующие пределу выносливости, миллионов циклов; NK 1, NK 2 – суммарные числа циклов напряжений, миллионов циклов. Базовые числа циклов напряжений шестерни и колеса, соответствующие пределу выносливости, рассчитываются по формулам NHlim 1 = 30 . NHlim 2 = 30 . Для шестерни NHlim 1 = 30 .300 Для колеса NHlim 2 = 30 .250 Суммарные числа циклов напряжений шестерни и колеса NK1 = 60 . n1.Lh, (3.13) NK2 = 60 . n2.Lh, (3.14) где n 1, n 2 – частоты вращения шестерни и колеса соответственно, об/мин; Lh – требуемый ресурс передачи, ч. NK 1 = 60.650.20000 =780. 106, NK 2 = 60.200.20000 =240. 106. Т.к. выполняются условия NK1 >NHlim1и NK2 >NHlim2, то коэффициенты долговечности рассчитываем по формуле (3.9)
Теперь можно рассчитать допускаемые контактные напряжения для материалов шестерни и колеса по формулам (3.5) и (3.6) соответственно
Найдём допускаемое контактное напряжение для косозубой передачи по формуле (3.4)
Тогда межосевое расстояние по формуле (3.2)
Модуль зубьев, мм
Значение модуля принимается из вычисленного интервала и согласовывается со стандартным: m = 2,5.
Сумма зубьев шестерни и колеса
где β = 13° – угол наклона линии зуба.
Число зубьев шестерни
Число зубьев колеса
Уточненное значение угла наклона зубьев, град.
Делительные диаметры шестерни и колеса, мм
Диаметры вершин зубьев шестерни и колеса, мм
Диаметры впадин зубьев, мм
Уточненное межосевое расстояние, мм
Рабочая ширина зубчатого венца, равная ширине венца колеса, мм
Ширина венца шестерни, мм
Окружная скорость зубчатых колес, м/с
Степень точности цилиндрической зубчатой передачи согласно ГОСТ 1643-81 равна 8. 3.2.1 Проверочный расчет зубьев колес на контактную прочность После определения геометрических размеров рабочие поверхности зубьев необходимо проверить на контактную прочность. Для этого следует определить рабочие контактное напряжение σн и сравнить с допускаемым σнр. Должно выполняться условие σн ≤ σнр. Рабочее контактное напряжение, МПа где Z Е = 190 – коэффициент, учитывающий механические свойства материалов сопряжённых зубчатых колёс, изготовленных из стали; ZH – коэффициент, учитывающий форму сопряжённых поверхностей зубьев в полюсе зацепления; Zε – коэффициент, учитывающий суммарную длину контактных линий прямозубой передачи; Ft 1 – окружная сила на делительном диаметре, Н; КА = 1,1 – коэффициент внешней динамической нагрузки при равномерном нагружении двигателя и ведомой машины; К HV – коэффициент, учитывающий динамическую нагрузку; К H β – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; К H α – коэффициент, учитывающий распределение нагрузки между зубьями. Коэффициент ZH рассчитывается по формуле
где α t – делительный угол профиля в торцовом сечении, град.; α tω – угол зацепления, град, для передач без смещения α tω = α t; b b – основной угол наклона, град.
Угол α t рассчитывается по формуле
где b – угол наклона линии зуба, град.
Угол bbрассчитывается по формуле
Рассчитаем коэффициент, учитывающий форму сопряжённых поверхностей зубьев в полюсе зацепления по формуле (3.31)
Коэффициент Zε рассчитывается по формуле
где εα – коэффициент торцового перекрытия, рассчитываемый по формуле
Окружная сила на делительном диаметре, Н
Коэффициент КHV рассчитывается по формуле где ω HV – удельная окружная динамическая сила, Н/мм. Сила ωHV рассчитывается по формуле
где δн = 0,02 – коэффициент, учитывающий влияние вида зубчатой передачи; q 0 = 5,6 (при m
Коэффициент KHβ рассчитывается по формуле
где
Коэффициент
где
Фактическое отклонение положения контактных линий в начальный период работы передачи
где
Удельная нормальная жесткость пары зубьев
где
Рассчитаем удельную нормальную жесткость пары зубьев по формуле (3.42):
Отсюда получаем С¢=17,241 Н/мм·мкм. Подставим полученные данные в формулу (3.40):
Коэффициент KHω рассчитывается по формуле
Рассчитаем формулу (3.39)
Коэффициент КНα рассчитывается по формуле
где
a a = 0,2 – коэффициент, учитывающий статистическое распределение погрешностей и критерии допустимого повреждения поверхностей зубьев;
Y a – уменьшение погрешности шага зацепления в результате приработки, мкм. Суммарный коэффициент перекрытия рассчитывается по формуле
где e b – коэффициент осевого перекрытия. Коэффициент торцового перекрытия
где
где
Коэффициент осевого перекрытия
где
Средняя удельная торцовая жесткость зубьев пары зубчатых колес
Предельное отклонение шага зацепления рассчитывается по формуле
где
Уменьшение погрешности шага зацепления в результате приработки
Коэффициент КНα по формуле (3.46)
Найдём рабочее контактное напряжение по формуле (3.30)
Допустимые напряжения более рабочих контактных на 2,58%, условие выполняется.
3.2.2 Расчет зубьев на прочность при изгибе
Выносливость зубьев, необходимую для предотвращения усталостного излома, устанавливаем для каждого колеса сопоставлением расчетного местного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения Расчетное местное напряжение при изгибе, МПа: где
Рисунок 3 – Диаграмма концентрации напряжений Коэффициент нагрузки
где Коэффициент
где Удельная окружная сила
где
Коэффициент
где
По полученным данным рассчитаем формулу (3.63)
Коэффициент, учитывающий наклон зуба
Коэффициент, учитывающий перекрытие зубьев (
Напряжения при изгибе для шестерни
Напряжения при изгибе для колеса
Допускаемые напряжения для шестерни и колеса соответственно, МПа
где
где d – диаметр делительной окружности зубчатого колеса, мм. Коэффициент YX1
Коэффициент YX2
Пределы выносливости зубьев при изгибе
где
Рассчитаем предел выносливости зубьев при изгибе по формулам (3.76), (3.77)
Допускаемые напряжения по формулам (3.72), (3.73)
Проверка выполнения условия 50,665 МПа ≤ 391,183 МПа. Проверка выполнения условия 47,8798 МПа ≤ 319,41 МПа. Условия выполняются.
|
||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (3.2)
(3.2)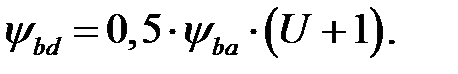 (3.3)
(3.3)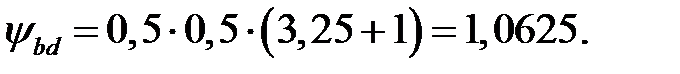
 (3.4)
(3.4) (3.5)
(3.5)  (3.6)
(3.6) ,
,  – пределы контактной усталости поверхностей зубьев, соответствующие базовому числу циклов напряжений шестерни и колеса, МПа;
– пределы контактной усталости поверхностей зубьев, соответствующие базовому числу циклов напряжений шестерни и колеса, МПа;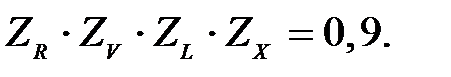
 (3.7)
(3.7)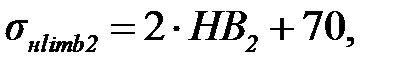 (3.8)
(3.8)

 (3.9)
(3.9)  (3.10)
(3.10)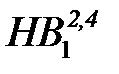 ≤ 120 . 106, (3.11)
≤ 120 . 106, (3.11) ≤ 120 . 106. (3.12)
≤ 120 . 106. (3.12) = 26,437×106 ≤ 120 . 106.
= 26,437×106 ≤ 120 . 106. = 17,068×106 ≤ 120 . 106.
= 17,068×106 ≤ 120 . 106.





 (3.15)
(3.15)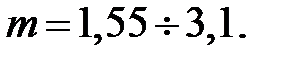
 (3.16)
(3.16)
 (3.17)
(3.17)
 (3.18)
(3.18)
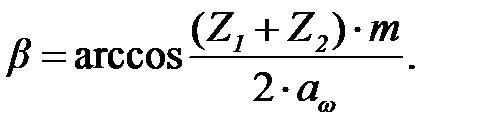 (3.19)
(3.19)
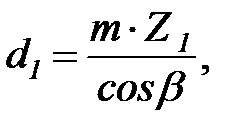 (3.20)
(3.20) (3.21)
(3.21)
 .
. (3.22)
(3.22)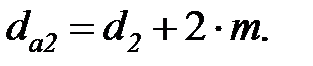 (3.23)
(3.23)
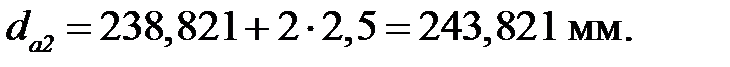
 (3.24)
(3.24)
 (3.25)
(3.25)
 (3.26)
(3.26)
 (3.27)
(3.27)
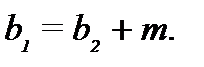 (3.28)
(3.28)
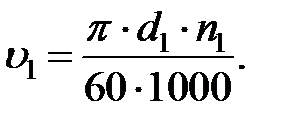 (3.29)
(3.29)
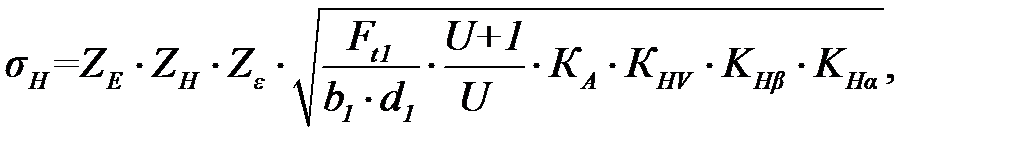 (3.30)
(3.30) (3.31)
(3.31) , (3.32)
, (3.32)
 (3.33)
(3.33)

 (3.34)
(3.34) (3.35)
(3.35)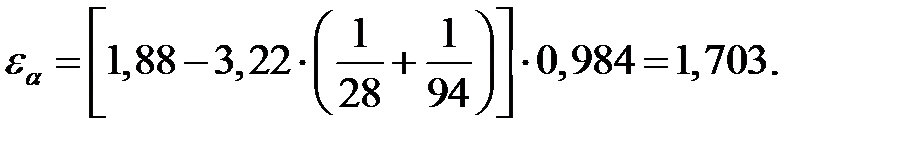
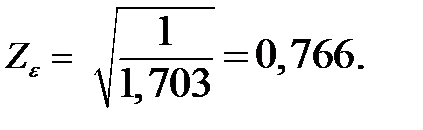
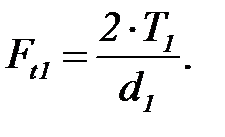 (3.36)
(3.36)
 (3.37)
(3.37)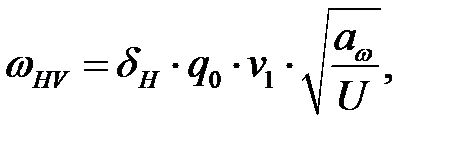 (3.38)
(3.38) 3,55 мм) – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса 8-й степени точности.
3,55 мм) – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса 8-й степени точности.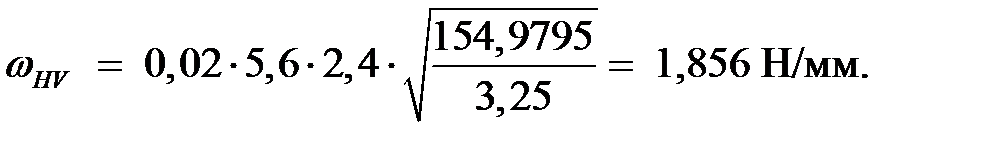

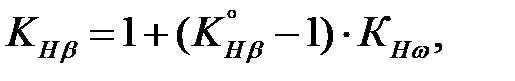 (3.39)
(3.39)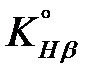 – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи;
– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи; – коэффициент, учитывающий приработку зубьев.
– коэффициент, учитывающий приработку зубьев.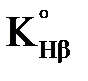 рассчитывается по формуле
рассчитывается по формуле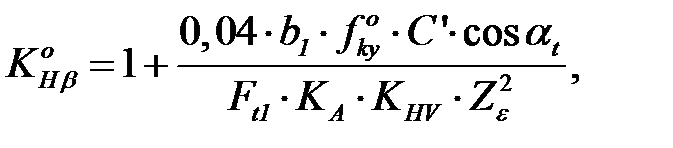 (3.40)
(3.40) – фактическое отклонение положения контактных линий в начальный период работы передачи;
– фактическое отклонение положения контактных линий в начальный период работы передачи; – удельная нормальная жесткость пары зубьев, Н/мм·мкм.
– удельная нормальная жесткость пары зубьев, Н/мм·мкм. (3.41)
(3.41)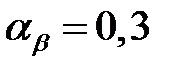 – коэффициент, учитывающий статистическое распределение погрешностей и критерий допустимого повреждения активных поверхностей зубьев;
– коэффициент, учитывающий статистическое распределение погрешностей и критерий допустимого повреждения активных поверхностей зубьев; – допуск на погрешность направления зубьев выбирается из таблицы П.3[2], мкм:
– допуск на погрешность направления зубьев выбирается из таблицы П.3[2], мкм: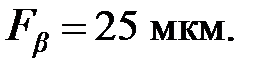

 (3.42)
(3.42) – эквивалентные числа зубьев шестерни и колеса соответственно, рассчитываемые по формулам
– эквивалентные числа зубьев шестерни и колеса соответственно, рассчитываемые по формулам (3.43)
(3.43)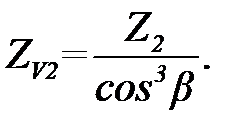 (3.44)
(3.44)



 (3.45)
(3.45)
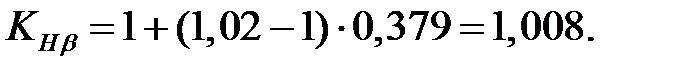
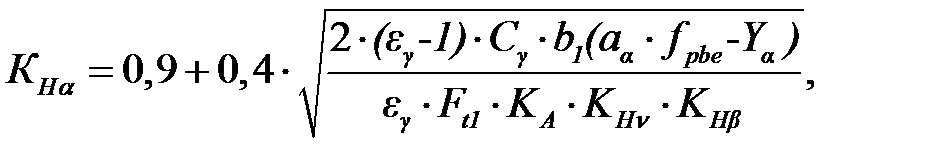 (3.46)
(3.46) суммарный коэффициент перекрытия;
суммарный коэффициент перекрытия; – средняя удельная торцовая жесткость зубьев пары зубчатых колес, Н/(мм·мкм);
– средняя удельная торцовая жесткость зубьев пары зубчатых колес, Н/(мм·мкм); – предельное отклонение шага зацепления, мкм;
– предельное отклонение шага зацепления, мкм;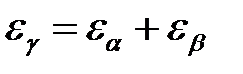 , (3.47)
, (3.47) – коэффициент торцового перекрытия;
– коэффициент торцового перекрытия; ; (3.48)
; (3.48) , (3.49)
, (3.49) (3.50)
(3.50)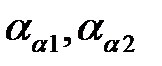 – углы профиля в точках на окружностях вершин, град,
– углы профиля в точках на окружностях вершин, град, , (3.51)
, (3.51) , (3.52)
, (3.52)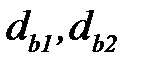 – основные диаметры шестерни и колеса, мм,
– основные диаметры шестерни и колеса, мм, , (3.53)
, (3.53) . (3.54)
. (3.54)

 °,
°,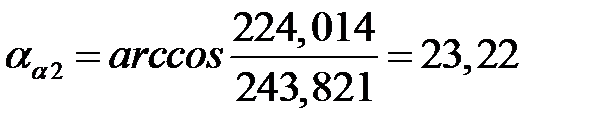 °.
°. ,
, .
. .
. , (3.55)
, (3.55) – осевой шаг, мм, рассчитываемый по формуле
– осевой шаг, мм, рассчитываемый по формуле . (3.56)
. (3.56)
 .
. (3.57)
(3.57) Н/(мм·мкм).
Н/(мм·мкм). , (3.58)
, (3.58) – предельные отклонения шага зацепления шестерни и колеса соответственно, мкм, выбираются согласно П.4[2]:
– предельные отклонения шага зацепления шестерни и колеса соответственно, мкм, выбираются согласно П.4[2]: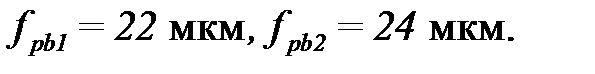
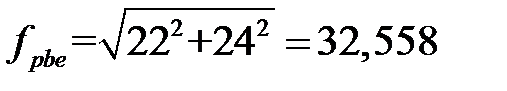 мкм.
мкм. ; (3.59)
; (3.59) , (3.60)
, (3.60) . (3.61)
. (3.61) мкм,
мкм, мкм.
мкм. мкм.
мкм.

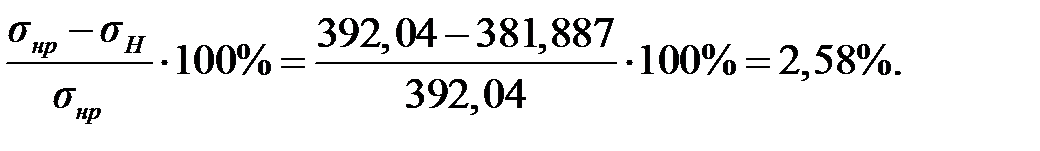

 , (3.62)
, (3.62) – коэффициент нагрузки;
– коэффициент нагрузки; – коэффициент, учитывающий форму зуба, концентрацию напряжений, определяется по диаграмме (рис.3) в зависимости от эквивалентного числа зубьев шестерни и колеса,
– коэффициент, учитывающий форму зуба, концентрацию напряжений, определяется по диаграмме (рис.3) в зависимости от эквивалентного числа зубьев шестерни и колеса, .
. – коэффициент, учитывающий наклон зуба;
– коэффициент, учитывающий наклон зуба; – коэффициент, учитывающий перекрытие зубьев.
– коэффициент, учитывающий перекрытие зубьев.
 , (3.63)
, (3.63) – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса,
– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса, – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии;
– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии; – коэффициент, учитывающий распределение нагрузки между зубьями,
– коэффициент, учитывающий распределение нагрузки между зубьями,  = 1,1022.
= 1,1022. , (3.64)
, (3.64) – удельная окружная сила, Н/мм.
– удельная окружная сила, Н/мм.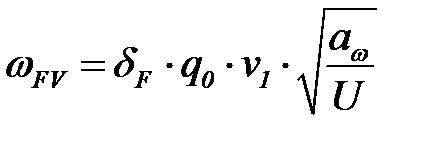 , (3.65)
, (3.65) = 0,06 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев.
= 0,06 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев. Н/мм.
Н/мм. .
. рассчитывается по формуле
рассчитывается по формуле , (3.66)
, (3.66) ; (3.67)
; (3.67) . (3.68)
. (3.68) .
. .
. .
. .
. . (3.69)
. (3.69) .
.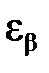 ≥ 1),
≥ 1), . (3.70)
. (3.70)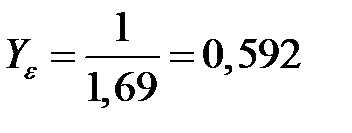 .
. ;
; . (3.71)
. (3.71)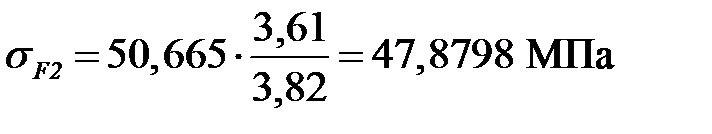 .
. , (3.72)
, (3.72)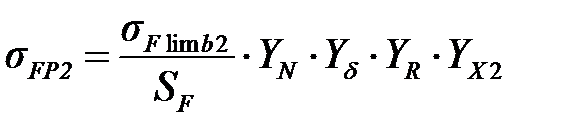 , (3.73)
, (3.73) – пределы выносливости зубьев при изгибе, МПа;
– пределы выносливости зубьев при изгибе, МПа; = 1,7 – коэффициент запаса прочности для углеродистой и легированной стали, подвергнутых нормализации или улучшению;
= 1,7 – коэффициент запаса прочности для углеродистой и легированной стали, подвергнутых нормализации или улучшению; = 1 – коэффициент долговечности;
= 1 – коэффициент долговечности;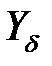 – коэффициент, учитывающий чувствительность материала к концентрации напряжений, рассчитываемый по формуле
– коэффициент, учитывающий чувствительность материала к концентрации напряжений, рассчитываемый по формуле . (3.74)
. (3.74) .
. = 1,2 – коэффициент, учитывающий шероховатость переходной поверхности (при нормализации и улучшении);
= 1,2 – коэффициент, учитывающий шероховатость переходной поверхности (при нормализации и улучшении); – коэффициенты, учитывающие размеры зубчатого колеса, рассчитываемые по формуле
– коэффициенты, учитывающие размеры зубчатого колеса, рассчитываемые по формуле , (3.75)
, (3.75)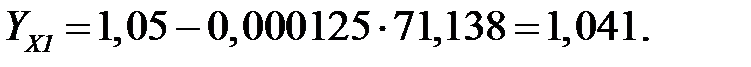

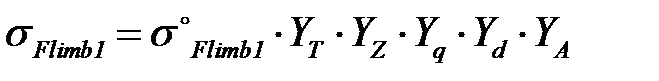 , (3.76)
, (3.76) , (3.77)
, (3.77)  – пределы выносливости зубьев, при изгибе, соответствующие базовому числу циклов напряжений, МПа, рассчитываемые по формуле
– пределы выносливости зубьев, при изгибе, соответствующие базовому числу циклов напряжений, МПа, рассчитываемые по формуле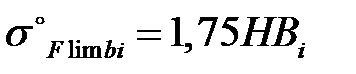 . (3.78)
. (3.78) ,
, .
. = 1 – коэффициент, учитывающий технологию изготовления зубчатых колес;
= 1 – коэффициент, учитывающий технологию изготовления зубчатых колес; = 1 – коэффициент, учитывающий способ получения заготовки зубчатого колеса (ковка или штамповка);
= 1 – коэффициент, учитывающий способ получения заготовки зубчатого колеса (ковка или штамповка); = 1 – коэффициент, учитывающий отсутствие шлифовки переходной поверхности зубьев;
= 1 – коэффициент, учитывающий отсутствие шлифовки переходной поверхности зубьев;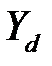 = 1 – коэффициент, учитывающий отсутствие деформационного упрочнения или электрохимической обработка переходной поверхности;
= 1 – коэффициент, учитывающий отсутствие деформационного упрочнения или электрохимической обработка переходной поверхности; = 1 – коэффициент, учитывающий влияние характера приложения нагрузки (одностороннее).
= 1 – коэффициент, учитывающий влияние характера приложения нагрузки (одностороннее). ,
, .
. ,
, .
. для шестерни
для шестерни


