Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последствия мультиколлинеарностиСодержание книги
Поиск на нашем сайте Последствия в случае строгой мультиколлинеарности: Оценки МНК не единственные. При наличии нестрогой мультиколлинеарности МНК–оценки формально существуют, основные предпосылки регрессионного анализа не нарушаются. Но при этом есть недостатки: 1. Оценки имеют большие стандартные ошибки, это приводит к следующим негативным последствиям: 1) небольшое изменение исходных данных (удаление/добавление) приводит к существенному изменению оценок регрессии, что делает модель непригодной для анализа и прогнозирования; 2) коэффициенты становятся незначимыми, хотя уравнение в целом значимо; 3) очень широкие доверительные интервалы; 2. Наличие коллинеарности затрудняет интерпретацию параметров множественной регрессии как характеристик факторов в «чистом» виде; параметры линейной регрессии теряют свой смысл; возможно получение неверного знака у коэффициента регрессии; 3. Затрудняется определение вклада каждой из объясняющей переменных в объяснимую уравнением регрессии дисперсию зависимой переменной.
Методы обнаружения мультиколлинеарности
Первый метод. Для обнаружения парной коллинеарности можно использовать матрицу парных коэффициентов корреляции:
Если значение коэффициента парной корреляции превышает значение 0,7, то это свидетельствует о коллинеарности между двумя факторами. Из двух коррелирующих факторов оставляют тот, который лучше коррелирует с результативным признаком. Второй метод. Расчет фактора инфляции дисперсии
Программа GRETL позволяет анализировать наличие мультиколлинеарности с помощью показателя Проявляться мультиколлинеарности может следующим образом: коэффициенты регрессии незначимы, но в целом уравнение регрессии статистически значимо. Если убрать незначимые коэффициенты, то модель резко ухудшается (коэффициент детерминации значительно снижается).
ПРАКТИЧЕСКОЕ ЗАДАНИЕ
В данной работе необходимо оценить множественное линейное уравнение регрессии зависимости стоимости квартиры от ее параметров на вторичном рынке недвижимости (см. Табл. 1). В выборку попали одно-, двух- и трехкомнатные квартиры в различных районах города Волгограда. Полная таблица статистических данных о 194 квартирах находятся в файле «LR4».
В таблице 1 введены следующие переменные: price – зависимая переменная, стоимость квартиры, тыс. руб. z – фиктивная переменная, показывающая на каком этаже находится квартира: z – фиктивная переменная, показывающая на каком этаже находится квартира:
 2) проверить модель на наличие мультиколлинеарности с помощью корреляционной матрицы 3) если в модели будет присутствовать мультиколлинеарность, то, чтобы ее устранить необходимо из модели исключить один из коррелирующих факторов. 4) для итоговой модели, в которой отсутствует мультиколлинеарность необходимо: сделать точечную и интервальную оценку параметров. рассчитать множественный коэффициент детерминации; найти скорректированный коэффициент детерминации проверить статистическую значимость уравнения регрессии в целом с помощью F-статистики.
Порядок выполнения задания
1. Загрузите таблицу с данными. Для этого нажмите на кнопку Файл, затем Открыть – Пользовательские. Появится диалоговое окно. Выберите тип файла: Все файлы. Укажите директорию, в которой находится файл с данными. Выберите необходимый файл. Нажмите открыть. Появится диалоговое окно:
Укажите Столбец – 1, Строка – 2. Нажмите ОК. В результате должен появиться список переменных:
2. Найдите параметры множественного линейного уравнения регрессии методом наименьших квадратов. В Меню выберите раздел Модель, затем перейдите на вкладку Метод наименьших квадратов. В новом диалоговом окне задайте зависимые переменные и регрессоры с помощью стрелок
Затем нажмите кнопку Появится таблица с результатами расчета основных показателей множественного линейного уравнения регрессии методом наименьших квадратов (МНК).
2. Запишите в таблицу 1 бланка отчета точечные оценки параметров множественного уравнения регрессии, а также коэффициент детерминации R 2 (R-квадрат), скорректированный коэффициент детерминации R 2 adj (Испр. R-квадрат), F -статистику (F(4, 189)) и P -значение.
3. Найдите доверительный интервал коэффициентов уравнения регрессии 95%-й надежностью. Для этого В окне с результатами МНК перейдите в раздел Анализ, а затем на вкладку Доверительные интервалы для коэффициентов. Появится таблица с результатами интервальной оценки. Запишите в таблицу 1 бланка отчета доверительный интервал. Сделайте предположение о значимости выборочных коэффициентов регрессии.
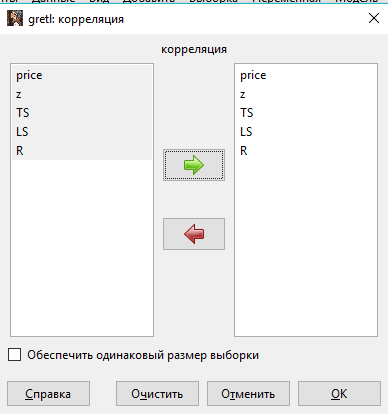
4. Найдите коэффициенты корреляции rxy. Для этого необходимо нажать кнопку Вид, затем Корреляционная матрица.
Выберите все переменные:
Нажмите ОК. Появится таблица с результатами. Запишите коэффициенты корреляции в таблицу 2. Если между факторными признаками коэффициент парной корреляции более 0,9, то это свидетельствует о мультиколлинеарности. В этом случае необходимо исключить один из коррелирующих регрессоров: тот, который имеет наименьшую корреляцию с результативным признаком.
5. После устранения мультиколлинеарности необходимо оценить новую модель (без факторного признака, который был удален!)
6. Заполните таблицу 3 для регрессионной модели без мультиколлинеарности.
7. Сделайте выводы относительно выборочных коэффициентов регрессии согласно их экономическому смыслу.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Сформулируйте понятие множественного уравнения регрессии. Приведите примеры. Множественное уравнение регрессии в матричной форме. 2. Каким необходимо следовать правилам при отборе факторов в уравнение регрессии. 3. Степенное и линейное уравнение множественной регрессии. Экономический смысл коэффициентов. Примеры использования степенных и линейных уравнений. 4. Множественный коэффициент детерминации. Скорректированный коэффициент детерминации. 5. Условия Гаусса-Маркова c детерминированными регрессорами. Теорема Гаусса-Маркова. 6. Проверка статистической значимости параметров множественного линейного уравнения регрессии (t -критерий), а также уравнения регрессии в целом (F -критерий). 7. Понятие мультиколлинеарности. Причины появления и последствия мультиколлинеарности. 8. Способы обнаружения и методы устранения мультиколлинеарности.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |


 (Variance Inflation Factor):
(Variance Inflation Factor):
 – это коэффициент детерминации для регрессии j-го регрессора от остальных. Можно считать, что мультикоолинеарность есть, если
– это коэффициент детерминации для регрессии j-го регрессора от остальных. Можно считать, что мультикоолинеарность есть, если 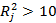 . Это примерное значение.
. Это примерное значение. ;
;

 и
и  .
.
 .
.