Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множественное уравнение регрессии.Стр 1 из 3Следующая ⇒ ЛАБОРАТОРНАЯ РАБОТА № 4 МНОЖЕСТВЕННОЕ УРАВНЕНИЕ РЕГРЕССИИ. МУЛЬТИКОЛЛИНЕАРНОСТЬ
Цель работы: построить на основе статистических данных с помощью программной среды GRETL множественное линейное уравнение регрессии, оценить качество модели.
Краткая теория Определение 1. Множественной регрессией называется з ависимость, при которой каждому набору нескольких переменных (регрессоров) соответствует определенное условное математическое ожидание зависимой переменной (результативного признака). Пример 1. 1) Урожайность какой–либо зерновой культуры зависит от сорта этой культуры, от количества внесенных удобрений, состава почвы, количества осадков, сроков уборки;2) вес человека зависит от его роста, объема грудной клетки, возраста;3) производительность труда – от стажа работы, уровня мастерства, автоматизации производства, электровооруженности предприятия и других факторов. Можно сказать, что множественная регрессия – это уравнение связи с несколькими переменными:
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии МНК. При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии. Множественное линейное уравнение регрессии для индивидуальных значений имеет вид:
В векторном виде множественное линейное уравнение регрессии можно записать:
Линейное уравнение регрессии можно записать лаконичнее, представив в матричном виде:
В данной формуле следующие обозначения:
Для уравнения
В матричном виде система нормальных уравнений примет вид:
При
В линейной множественной регрессии Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования уравнения регрессии для описания, анализа и прогнозирования. При отборе факторов, включаемых во множественную регрессию необходимо придерживаться следующих требований: 1) Число объясняющих переменных должно быть в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то параметры уравнения регрессии становятся статистически незначимыми. 2) Включаемые во множественную регрессию факторы должны объяснить вариацию зависимой переменной. Если строится модель с набором m факторов, то для нее рассчитывается показатель детерминации При дополнительном включении в уравнение регрессии факторов коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, и данные показатели практически не отличаются друг от друга, то включаемый в анализ дополнительный фактор не улучшает модель и является лишним. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по критерию Стьюдента. 3) Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, то ему нужно придать количественную определенность: проранжировать его или оценить в баллах. 4) Факторы не должны быть взаимокоррелированными и, тем более, находиться в точной функциональной связи. Считается, что две объясняющие переменные Если две или несколько объясняющих переменных в уравнении регрессии коррелируют между собой, то такое явление называется мультиколлинеарностью. Мерой общего качества уравнения множественной регрессии является коэффициент детерминации:
Коэффициент детерминации определяет долю разброса зависимой переменной, объясняемую полученным (эмпирическим) уравнением регрессии. Формула скорректированного коэффициента множественной детерминации имеет вид:
Чем больше объем совокупности, по которой исчислена регрессия, тем меньше различаются показатели Однако увеличение Пример 2.
Видно, что если третий столбец разделить на два, то получится в точности второй столбец.
Пример 3. По группе лиц женского и мужского пола изучается линейная зависимость потребления кофе Уравнение регрессии:
где
Таким образом, в общем уравнении регрессии переменная ПРАКТИЧЕСКОЕ ЗАДАНИЕ
В данной работе необходимо оценить множественное линейное уравнение регрессии зависимости стоимости квартиры от ее параметров на вторичном рынке недвижимости (см. Табл. 1). В выборку попали одно-, двух- и трехкомнатные квартиры в различных районах города Волгограда. Полная таблица статистических данных о 194 квартирах находятся в файле «LR4».
В таблице 1 введены следующие переменные: price – зависимая переменная, стоимость квартиры, тыс. руб. z – фиктивная переменная, показывающая на каком этаже находится квартира: z – фиктивная переменная, показывающая на каком этаже находится квартира:
 2) проверить модель на наличие мультиколлинеарности с помощью корреляционной матрицы 3) если в модели будет присутствовать мультиколлинеарность, то, чтобы ее устранить необходимо из модели исключить один из коррелирующих факторов. 4) для итоговой модели, в которой отсутствует мультиколлинеарность необходимо: сделать точечную и интервальную оценку параметров. рассчитать множественный коэффициент детерминации; найти скорректированный коэффициент детерминации проверить статистическую значимость уравнения регрессии в целом с помощью F-статистики.
Порядок выполнения задания
1. Загрузите таблицу с данными. Для этого нажмите на кнопку Файл, затем Открыть – Пользовательские. Появится диалоговое окно. Выберите тип файла: Все файлы. Укажите директорию, в которой находится файл с данными. Выберите необходимый файл. Нажмите открыть. Появится диалоговое окно:
Укажите Столбец – 1, Строка – 2. Нажмите ОК. В результате должен появиться список переменных:
2. Найдите параметры множественного линейного уравнения регрессии методом наименьших квадратов. В Меню выберите раздел Модель, затем перейдите на вкладку Метод наименьших квадратов. В новом диалоговом окне задайте зависимые переменные и регрессоры с помощью стрелок
Затем нажмите кнопку Появится таблица с результатами расчета основных показателей множественного линейного уравнения регрессии методом наименьших квадратов (МНК).
2. Запишите в таблицу 1 бланка отчета точечные оценки параметров множественного уравнения регрессии, а также коэффициент детерминации R 2 (R-квадрат), скорректированный коэффициент детерминации R 2 adj (Испр. R-квадрат), F -статистику (F(4, 189)) и P -значение.
3. Найдите доверительный интервал коэффициентов уравнения регрессии 95%-й надежностью. Для этого В окне с результатами МНК перейдите в раздел Анализ, а затем на вкладку Доверительные интервалы для коэффициентов. Появится таблица с результатами интервальной оценки. Запишите в таблицу 1 бланка отчета доверительный интервал. Сделайте предположение о значимости выборочных коэффициентов регрессии.
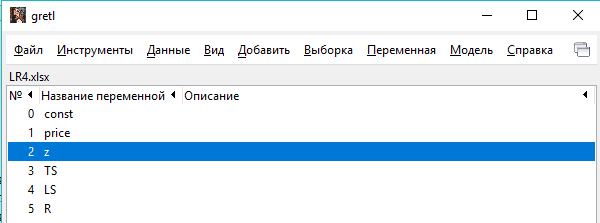
4. Найдите коэффициенты корреляции rxy. Для этого необходимо нажать кнопку Вид, затем Корреляционная матрица.
Выберите все переменные:
Нажмите ОК. Появится таблица с результатами. Запишите коэффициенты корреляции в таблицу 2. Если между факторными признаками коэффициент парной корреляции более 0,9, то это свидетельствует о мультиколлинеарности. В этом случае необходимо исключить один из коррелирующих регрессоров: тот, который имеет наименьшую корреляцию с результативным признаком.
5. После устранения мультиколлинеарности необходимо оценить новую модель (без факторного признака, который был удален!)
6. Заполните таблицу 3 для регрессионной модели без мультиколлинеарности.
7. Сделайте выводы относительно выборочных коэффициентов регрессии согласно их экономическому смыслу.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Сформулируйте понятие множественного уравнения регрессии. Приведите примеры. Множественное уравнение регрессии в матричной форме. 2. Каким необходимо следовать правилам при отборе факторов в уравнение регрессии. 3. Степенное и линейное уравнение множественной регрессии. Экономический смысл коэффициентов. Примеры использования степенных и линейных уравнений. 4. Множественный коэффициент детерминации. Скорректированный коэффициент детерминации. 5. Условия Гаусса-Маркова c детерминированными регрессорами. Теорема Гаусса-Маркова. 6. Проверка статистической значимости параметров множественного линейного уравнения регрессии (t -критерий), а также уравнения регрессии в целом (F -критерий). 7. Понятие мультиколлинеарности. Причины появления и последствия мультиколлинеарности. 8. Способы обнаружения и методы устранения мультиколлинеарности. ЛАБОРАТОРНАЯ РАБОТА № 4 МНОЖЕСТВЕННОЕ УРАВНЕНИЕ РЕГРЕССИИ. МУЛЬТИКОЛЛИНЕАРНОСТЬ
Цель работы: построить на основе статистических данных с помощью программной среды GRETL множественное линейное уравнение регрессии, оценить качество модели.
Краткая теория Определение 1. Множественной регрессией называется з ависимость, при которой каждому набору нескольких переменных (регрессоров) соответствует определенное условное математическое ожидание зависимой переменной (результативного признака). Пример 1. 1) Урожайность какой–либо зерновой культуры зависит от сорта этой культуры, от количества внесенных удобрений, состава почвы, количества осадков, сроков уборки;2) вес человека зависит от его роста, объема грудной клетки, возраста;3) производительность труда – от стажа работы, уровня мастерства, автоматизации производства, электровооруженности предприятия и других факторов. Можно сказать, что множественная регрессия – это уравнение связи с несколькими переменными:
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии МНК. При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии. Множественное линейное уравнение регрессии для индивидуальных значений имеет вид:
В векторном виде множественное линейное уравнение регрессии можно записать:
Линейное уравнение регрессии можно записать лаконичнее, представив в матричном виде:
В данной формуле следующие обозначения:
Для уравнения
В матричном виде система нормальных уравнений примет вид:
При
В линейной множественной регрессии Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования уравнения регрессии для описания, анализа и прогнозирования. При отборе факторов, включаемых во множественную регрессию необходимо придерживаться следующих требований: 1) Число объясняющих переменных должно быть в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то параметры уравнения регрессии становятся статистически незначимыми. 2) Включаемые во множественную регрессию факторы должны объяснить вариацию зависимой переменной. Если строится модель с набором m факторов, то для нее рассчитывается показатель детерминации При дополнительном включении в уравнение регрессии факторов коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, и данные показатели практически не отличаются друг от друга, то включаемый в анализ дополнительный фактор не улучшает модель и является лишним. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по критерию Стьюдента. 3) Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, то ему нужно придать количественную определенность: проранжировать его или оценить в баллах. 4) Факторы не должны быть взаимокоррелированными и, тем более, находиться в точной функциональной связи. Считается, что две объясняющие переменные Если две или несколько объясняющих переменных в уравнении регрессии коррелируют между собой, то такое явление называется мультиколлинеарностью. Мерой общего качества уравнения множественной регрессии является коэффициент детерминации:
Коэффициент детерминации определяет долю разброса зависимой переменной, объясняемую полученным (эмпирическим) уравнением регрессии. Формула скорректированного коэффициента множественной детерминации имеет вид:
Чем больше объем совокупности, по которой исчислена регрессия, тем меньше различаются показатели Однако увеличение
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 1177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.244 (0.006 с.) |
 (1)
(1) – зависимая переменная;
– зависимая переменная;  – регрессоры.
– регрессоры.


 ;
;  ;
;  ;
; система нормальных уравнений имеет вид:
система нормальных уравнений имеет вид:

 эта система имеет единственное решение и МНК-оценки параметров линейной модели регрессии равны:
эта система имеет единственное решение и МНК-оценки параметров линейной модели регрессии равны:
 параметры при
параметры при  называются коэффициентами «чистой регрессии». Коэффициенты «чистой регрессии» характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне. Свободный член
называются коэффициентами «чистой регрессии». Коэффициенты «чистой регрессии» характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне. Свободный член  не подлежит экономической интерпретации. Его роль сводится к тому, что он вбирает в себя информацию о прочих не учитываемых в модели факторах. Формально его значение предполагает то значение объясняемой переменной, когда все
не подлежит экономической интерпретации. Его роль сводится к тому, что он вбирает в себя информацию о прочих не учитываемых в модели факторах. Формально его значение предполагает то значение объясняемой переменной, когда все  .
. , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как
, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как  .
. и
и  явно коллинеарны, т.е. находятся между собой в линейной зависимости, если коэффициент корреляции между ними
явно коллинеарны, т.е. находятся между собой в линейной зависимости, если коэффициент корреляции между ними  . Предпочтение отдается при этом не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
. Предпочтение отдается при этом не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. , (8)
, (8)
 и
и  . В статистических пакетах прикладных программ в процедуре множественной регрессии обычно приводится скорректированный коэффициент множественной детерминации. Величина коэффициента множественной детерминации используется для оценки качества регрессионной модели. Низкое значение коэффициента детерминации означает, что в регрессионную модель не включены существенные факторы – с одной стороны, а с другой стороны – рассматриваемая форма связи не отражает реальные соотношения между переменными, включенными в модель. В этом случае требуются дальнейшие исследования по улучшению качества модели и увеличению ее практической значимости.
. В статистических пакетах прикладных программ в процедуре множественной регрессии обычно приводится скорректированный коэффициент множественной детерминации. Величина коэффициента множественной детерминации используется для оценки качества регрессионной модели. Низкое значение коэффициента детерминации означает, что в регрессионную модель не включены существенные факторы – с одной стороны, а с другой стороны – рассматриваемая форма связи не отражает реальные соотношения между переменными, включенными в модель. В этом случае требуются дальнейшие исследования по улучшению качества модели и увеличению ее практической значимости.
 от цены
от цены  .
. (9)
(9) и
и 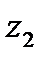 – фиктивные переменные, принимающие значения:
– фиктивные переменные, принимающие значения: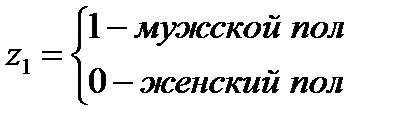 ,
,  (10)
(10) зависит не только от цены
зависит не только от цены  , но и от пола (
, но и от пола ( . Это ситуация совершенной мультиколлинеарности.
. Это ситуация совершенной мультиколлинеарности. ;
;

 и
и  .
.
 .
.